GPT-4诞生以来,无数人猜测它的出现可能意味着人类科技的一次颠覆性进步。那么人工智能的极限究竟在哪里呢?它可以为人类解决什么问题?本文从计算的角度,探讨了人工智能可能在数学的领域开发的极限在哪里。GPT-4如何突破其计算的边界?看完这篇文章,或许会对你有所启发。

GPT-4这个人人嘴里都在提到的词,已经成为了我们生活中一种社交货币。打开手机的那个瞬间,新闻媒体铺天盖地的,“GPT-4将取代的100种工作”、“GPT-4老板:AI可能会杀死人类”、“颠覆人类社会、改变人类”。
不了解人工智能的人们开始到处铺天盖地的说,甚至可能连GPT-4、文心一言相关的工具都没体验过,就开始到处跟风。甚至一些从业者也是故意放大,完全忘记了计算机的能力是有数学上的边界的。
这个边界就像是,我们目前所在的世界无法超越光速,我们无法看到四维、甚至更多维的世界一样。边界的意思是,我们需要知道我们能解决掉的问题有哪些,而不是无所不能漫无目的,人工智能、GPT都是一样的,我只有看见边界,我们才会想着如何突破。
接下来的几个问题非常的经典,我尽可能用简洁通俗的语言,结合图灵划定的计算机可计算的问题边界、希尔伯特第十问题一起探讨GPT未来计算的边界及发展方向,来探讨人工智能的边界所在。
一、图灵划定的计算机可计算的问题边界?
图灵(Alan Turing)是20世纪最伟大的数学家和计算机科学家之一,被称为计算机及人工智能之父。 图灵机被认为是当代计算机的理论基础,图灵对计算机可计算问题的界限的研究成为了计算机科学的里程碑。
他提出了著名的图灵停机问题,即判断一台计算机是否能在有限时间内停机,这一问题被证明是不可解的。这意味着,计算机存在一些问题是无法解决的,无论使用什么算法或方法,都不可能得到正确的答案。
这也就是说,图灵划定的计算机可计算的问题边界,是在计算机科学中非常重要的一个概念。虽然我们现在已经有了许多高级的计算机技术,但在图灵的思想中,计算机的边界是存在的。
计算机能够处理的问题边界是什么呢?图灵在他的著作《论计算机机器与智能》中提出了“可计算问题”的概念。简单来说,就是只有能够用有限的规则和步骤来解决的问题,计算机才能够处理。这也被称为“图灵可计算问题”的边界。
那么,这个边界究竟有多大呢?实际上,图灵可计算问题的范围非常广泛,几乎覆盖了所有日常生活中可能遇到的问题。这些问题包括数学运算、逻辑推理、语言翻译、图像处理等等。
可以说,几乎所有能够用数学语言来描述的问题,都可以被计算机所处理。 为了更好地理解图灵可计算问题的范围,我们可以看一下其中的一些具体案例。例如,计算机可以进行加减乘除、求平方根、对数函数等数学运算,可以进行图像处理、视频剪辑、音频合成等多媒体处理,可以进行语音识别、自然语言处理、机器翻译等语言处理,可以进行模拟、仿真、优化等工程计算。
可以说,这些问题的解决,离不开计算机的强大计算能力。 但是,图灵可计算问题并不是没有限制的。图灵在他的论文中也提到,存在一些问题是不可计算的。
例如,某些算法的运行时间可能会超过宇宙的寿命,这些问题是无法被计算机所处理的。此外,图灵还提出了著名的“停机问题”,即判断一个程序是否会在有限时间内停止运行的问题,这也被证明是不可计算的。这些问题的存在,也为计算机科学的发展带来了挑战。
图灵还证明了一个著名的“停机问题”(Halting Problem),即无法设计一个程序,能够判断另一个程序是否会在有限时间内停止运行。这个问题在计算机科学领域中具有重要意义,也表明了计算机存在一些问题是无法解决的。
尽管图灵机理论已经有了几十年的历史,但它仍然对计算机科学和人工智能领域的研究产生了深远的影响。在现代计算机科学中,图灵机理论仍然是理论计算模型的基础,并且在设计和优化计算机算法时也经常被引用。
总之,图灵机理论的重要性在于它提供了一种关于计算机可计算问题的理论基础,同时也揭示了一些计算机无法解决的问题。
它为计算机科学和人工智能的发展奠定了重要的基础,对于我们理解和应用计算机科学具有重要的指导意义。
二、希尔伯特第十问题,划定有解数学问题的边界?
希尔伯特是德国著名的数学家,被誉为“20世纪最杰出的数学家之一”。他是现代数学的奠基人之一,对数学的发展做出了极为重要的贡献。
希尔伯特在数学领域涉及广泛,尤其擅长代数学、数论、函数论等多个领域。他提出了著名的“希尔伯特问题”,这是一系列有关数学基础问题的未解决问题,其中第十个问题被认为是一个里程碑式的问题。
希尔伯特第十问题是数学中的一个开放问题,也是人工智能领域的一个关键问题。该问题主要涉及到代数学中的一个重要概念:代数曲面。该问题要求确定任何代数曲面是否可以由有限数量的整数系数方程组合成。
在1930年代,希尔伯特提出了23个重要的数学问题,其中第十个问题就是希尔伯特第十问题。经过数学家们的不断努力和研究,最终该问题被证明是不可解的,也就是说,不存在一种通用的算法可以解决这个问题。
希尔伯特第十问题。这个问题听起来很高深,但是其实跟我们日常生活息息相关,是数学中的一个经典问题,也是数学家们长期以来探索无穷的一个缩影。 首先,让我们来了解一下什么是希尔伯特第十问题。
简单来说,就是问有没有一个通用的方法可以证明所有的代数方程都可以通过有限次加、减、乘、除和根号运算来解决。 这个问题的背景是,19世纪末20世纪初,数学家们在研究代数方程时发现,尽管代数方程的根可以用有理数和根号表达,但是在一些情况下,需要用到更高级别的数学工具才能得到解。
例如,方程x^5 – x + 1 = 0的解不能用根号表达,需要用到椭圆函数才能得到解。因此,希尔伯特提出了这个问题,想要找到一种通用的方法,以便证明所有的代数方程都可以用加、减、乘、除和根号来解决。
然而,这个问题却在长达70年的时间里成为了数学家们的一个困扰。直到1970年,苏联数学家沙芬和美国数学家特莱菲一起,独立证明了希尔伯特第十问题的否定性,即不存在一个通用的方法来解决所有的代数方程。
那么,希尔伯特第十问题的否定性证明意味着什么呢?它意味着代数方程的解法是有限的,而不是无限的。同时,它也证明了数学中的无穷性并非所有时候都是可达到的,有些问题是无法解决的。这个证明引起了数学界的轰动,也为今后的数学研究提供了一个新的方向和思路。
可以参考下面的这张图,第十问题的解决,我们知道很多问题是我们不知道是否有解,是无法判断的问题,这些问题比有答案的问题多的多,也就意味着我们无法通过计算来解决他们。
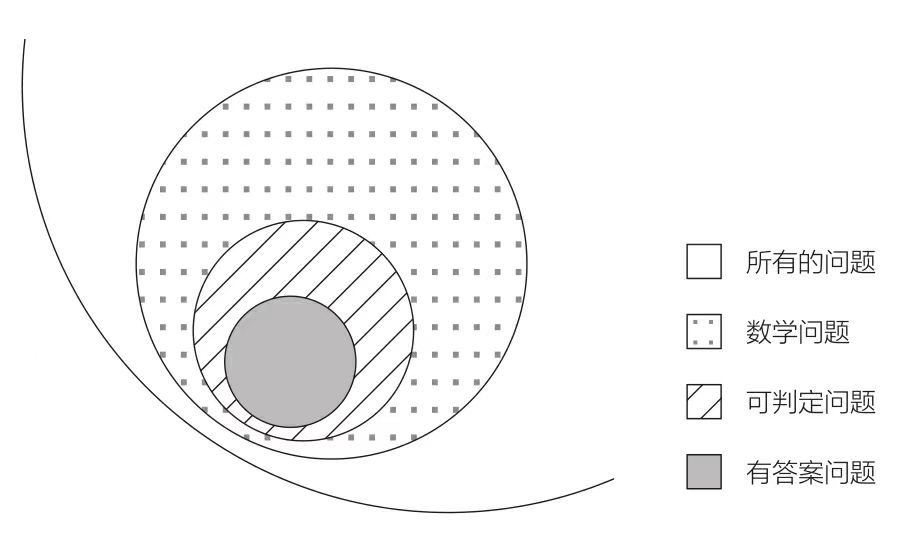
那么,我们回到日常生活中,这个问题又有什么用处呢?实际上,希尔伯特第十问题的研究背后,是数学家们对数学的一种探索和追求。通过这个问题的研究,数学家们能够更深入地理解数学中的一些基本概念和方法,例如代数学和数论等。同时,它也为数学在应用领域中的发展提供了基础。
比如,在密码学、通讯技术、信号处理等领域,需要用到代数方程的求解和理论,而希尔伯特第十问题的研究则为这些应用提供了理论基础。 除此之外,希尔伯特第十问题的研究还影响了许多其他领域,例如计算机科学、哲学等。
在计算机科学领域,希尔伯特第十问题被认为是算法设计中的一个重要问题,其背后的思想和方法也被广泛应用于计算机程序设计和软件开发等方面。在哲学领域,希尔伯特第十问题的否定性证明,引发了对数学和人类思维的一些深刻思考,也为哲学中的一些问题提供了新的启示和方向。
今天人工智能所解决的问题,只是有答案的数学问题中很小的一部分。
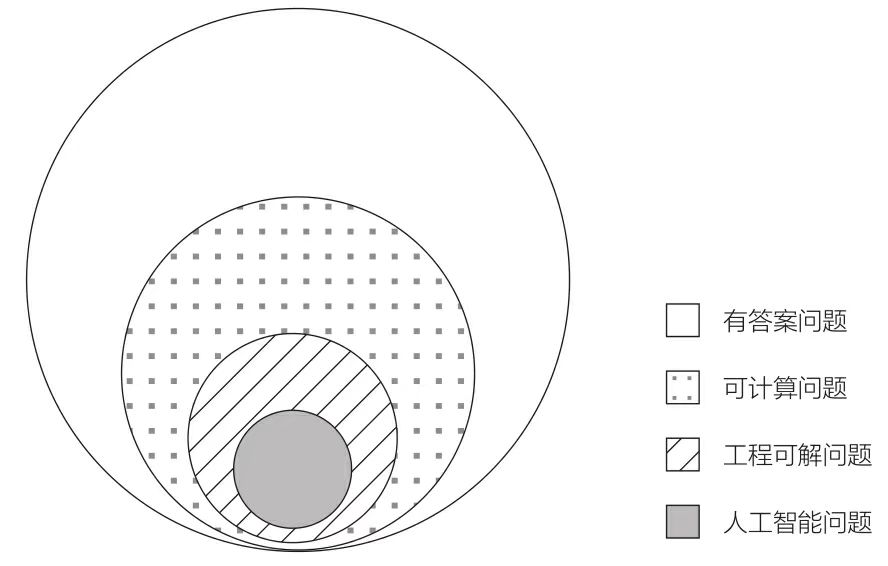
最后,让我们来总结一下希尔伯特第十问题的重要性。它是数学史上的一个经典问题,对数学领域的发展和人类对数学的认识都产生了重大影响。
同时,它也是我们思考数学、科学和人类思维的一个缩影,为我们带来了许多启示和思考。 通过学习希尔伯特第十问题,我们能够更深入地了解数学领域中的一些重要问题和理论,也能够更好地理解数学与其他领域的关联和应用。因此,我们应该保持对数学的好奇心和探索精神,不断地探索数学的无限可能。
三、GPT-4未来计算的边界及突破的发展方向?
GPT-4的算力和训练数据 首先,我们需要考虑GPT-4所需要的计算能力和训练数据。GPT-3目前已经是目前最大的语言模型之一,它拥有1750亿个参数,并使用了数十亿个单词和短语作为训练数据。
GPT-4相比之下需要更多的计算能力和更大的训练数据来实现更加强大的自然语言处理能力。 据报道,OpenAI已经在准备GPT-4的训练。目前,OpenAI已经开发了一种新的训练方法,可以有效地利用更多的计算资源和训练数据。OpenAI还在不断地探索新的算法和技术来提高训练效率和模型的性能。
那么,GPT-4及其他类似的AI技术的能力确实在不断突破,但是它们在数学商的边界上是否有突破的可能性呢?这个问题也是值得探讨的。 我们来了解一下GPT-4的能力。
GPT-4是基于深度学习技术的神经网络模型,它可以自动学习语言规律,理解语言的含义,并生成自然语言文本。相比之前的模型,GPT-4的规模更大、参数更多,拥有更强的处理能力,能够实现更复杂的自然语言任务,比如问答、机器翻译、摘要生成等。
然而,GPT-4并不能突破计算机在数学上的边界。计算机的本质是一台能够执行指令的机器,它的运算能力是有限的。图灵在20世纪30年代提出了“停机问题”,即判断一个程序是否会在有限时间内停机。
他证明了不存在一个通用算法能够解决所有的停机问题,也就是说,计算机是无法解决所有的数学问题的。 类似的,希尔伯特第十问题规定了一个数学问题的边界,即一个多项式方程是否存在有限项的解。该问题被证明是不可判定的,意味着计算机不能通过任何通用算法来判断一个多项式方程是否存在有限项的解。 另外,计算机的计算能力是基于算法的。
虽然GPT-4可以自动学习语言规律,但它并不能自己发明新的算法,也无法理解数学的本质。因此,它的计算能力仍然受限于现有的算法和数据。
总结来说: 在数学中,图灵划定的计算机可计算的问题边界以及希尔伯特第十问题是摆在人们面前的两大边界问题,GPT-4等类似的AI技术可以用于解决一些具有结构的数学问题,例如计算导数、积分和微分方程等。
这些问题通常可以用数值方法解决,而AI技术可以通过学习大量的数据和规则来实现更高效的计算。 然而,对于那些没有明显结构的数学问题,AI技术的应用可能会受到限制。这些问题通常需要进行创造性的思考和推理,而AI技术目前还不能像人类那样进行创造性的思考和推理。
例如,希尔伯特第十问题就是一个没有明显结构的数学问题,直到格里戈里·佩雷尔曼证明了庞加莱猜想,才有了对该问题的解答。
那么GPT-4会有哪些突破性的发展方向呢?
以下是一些可能的方向:
- 更好的语言理解能力:GPT-4可能会更好地理解语言,能够更准确地识别语言中的含义和语境,并且能够根据不同的语境进行合理的推理。
- 更强的多模态处理能力:GPT-4可能会更好地处理多模态数据,例如图片、声音和视频。它可以将自然语言和多媒体数据结合起来,实现更加智能的交互和应用。
- 更强的推理和创造能力:GPT-4可能会更强大地支持推理和创造能力。它可以更好地理解和处理复杂的语言和思维结构,并且可以自动生成更加有创意和新颖的文本。
四、GPT-4与量子计算机之间关系?
首先,我们需要了解GPT-4和量子计算机分别是什么。GPT-4是一种基于深度学习的自然语言处理模型,由于其能够自动生成高质量的文章、对话等自然语言,广泛应用于自动文本摘要、机器翻译、语音识别等领域。
而量子计算机是一种基于量子力学原理设计的计算机,使用量子比特(qubit)而非传统二进制位(bit)来存储和处理信息,可以处理传统计算机难以解决的一些问题,比如大规模的数据搜索、因子分解等。
然而,GPT-4和量子计算机并不是一对竞争关系。事实上,两者有很大的互补性。在理论层面,量子计算机可以在很大程度上优化GPT-4的计算效率。由于量子计算机具有并行处理的能力,可以更快地处理GPT-4中涉及到的大量数据,从而提高其计算速度和效率。
另一方面,在应用层面,GPT-4可以为量子计算机提供更加便捷的编程方式。量子计算机的编程难度较高,需要具备一定的物理学、数学知识。而GPT-4可以通过自动编码的方式,简化量子计算机的编程难度,使得更多人能够参与其中。
实际上,GPT-4与量子计算机之间的合作已经开始了。在2019年,加拿大滑铁卢大学和谷歌合作,利用GPT-2模型生成量子电路的代码。这项工作的目的是为了让更多的研究人员能够快速地生成量子电路的代码,从而推动量子计算机的发展。
随着科技的发展,我们也可以看到计算机在数学领域的发展。量子计算机作为一种新型计算机,具有超出传统计算机的运算能力,可以实现一些传统计算机无法实现的问题。
例如,Shor算法可以利用量子计算机解决大质数分解问题,这在传统计算机上是非常困难的。 未来,随着量子计算机技术的进一步发展,我们也许能够看到计算机在数学上的突破。但是,这需要更多的时间和研究。
在此之前,我们还需要依靠人类的智慧和创造力来推动数学和科技的发展。
五、总结
- 图灵和希尔伯特第十问题划定了数学的边界,人工智能也在其中,AI不是无所不能;
- 今天人工智能所解决的问题,只是有答案的数学问题中很小的一部分,现有的知识只是冰山一角;
- 量子计算机作为一种新型计算机,或许结合GPT-4能在数学的边界上获得突破。




 ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง
ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง





