不存在的事情也可以證明？一起體會數學證明的美麗之處！——《數學大觀念》

研究數學時，有一點非常有趣，那就是你可以證明一件事情千真萬確毋庸置疑，這也正是讓數學和其他科學有所不同的原因。

在其他的科學中，我們會因為一些法則符合現實世界的情況而接受它們，但是如果新的證據出現了，這些法則是可以被反駁或是修改的。然而在數學中，一旦某個理論被證實，它就是永遠真實不變的。舉例來說，歐幾里德在兩千年前證明出「質數有無限多個」，我們便無法再說什麼或做什麼來反駁這個理論的真實性。

科技來來去去，但是定理亙古不變。正如一位偉大的數學家哈代所說

數學家其實就像畫家或詩人，大家都在創造規律，但如果數學家創造出來的規律更永恆不朽，那是因為背後是由理念所建構而成。

對我來說，證明出一個新的數學定理似乎就是讓學術地位不朽的最佳途徑。

不存在的事也可以證明

數學不僅能證明某事絕對正確，也能用來證明某事絕無可能。

有時候，人們會說：「你無法證明不存在的事情不存在。」我想這大概就是說你無法證明世界上並沒有紫色的牛，因為可能哪天突然就會出現一隻。

但是在數學中，不存在是可以被證明的。舉例來說，不論你多麼努力嘗試，永遠都不可能找到相加會變成一個奇數的兩個偶數，也不可能找到一個最大的質數。

在你第一次（甚或第二或第三次）遇上這些證明時可能會覺得有點嚇人，所以絕對需要一點時間來適應。不過一旦掌握到了訣竅，你在閱讀和寫出這些證明的時候都會變得相當有趣。好的證明就像一個講得很精采的笑話或是故事，會讓你對結局非常滿意。

被遮住的淺色方格

跟你說說我第一次證明某事不可能的經驗。當我還小的時候，很喜歡各種遊戲和謎題。有天，一位朋友拿了一個遊戲裡的謎題來挑戰我，想當然我很感興趣啦。他出示一個八乘八的空白棋盤，然後拿出了 32 張一乘二大小的骨牌。

他問：「你能用這32 張骨牌將這個棋盤鋪滿嗎？」我說：「那當然，只要每一排放上四張骨牌就行了，就像這樣。」

用骨牌將八乘八的棋盤撲滿。圖／數學大觀念

「非常好，」他說，「現在假設我將左上角和右下角的正方形移開了，」他在這兩個方格中各放一枚硬幣，這樣我就不能使用了。「現在你能夠用 31 張骨牌鋪滿剩下的 62 個方格嗎？」

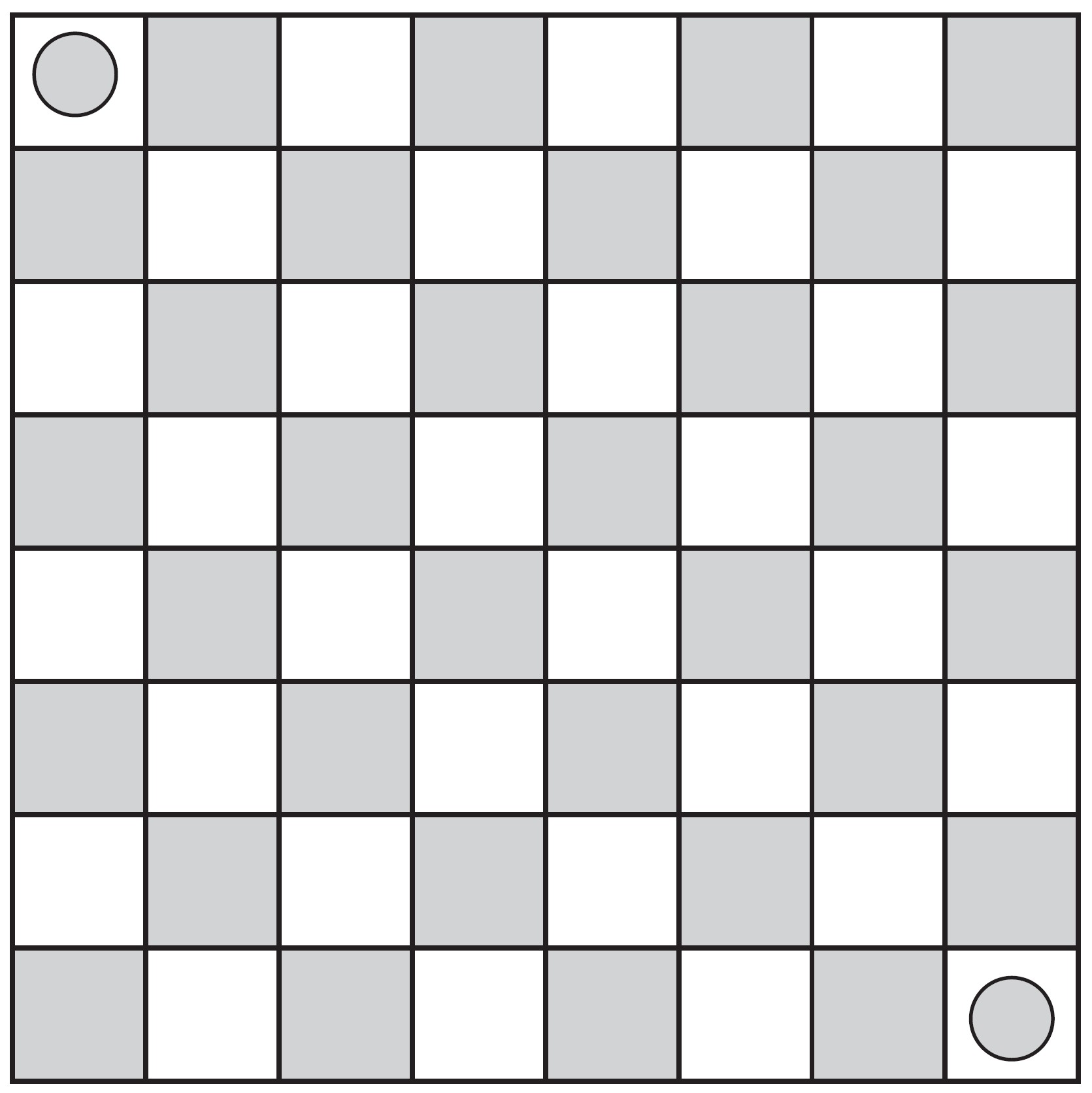移走兩個對角的方格後，能否還用骨牌將其補滿？圖／數學大觀念

「或許可以，」我說。

但無論我怎麼嘗試，就是無法達成，我開始思考這是否根本就不可行。

「如果你認為這不可行，你能夠證明這一點嗎？」我的朋友這麼問。但如果我沒有將無數失敗的可能都試過一遍，又怎麼能證明這是不可能的呢？

他隨後提出建議：「看看棋盤上的顏色。」顏色？顏色跟這一切有什麼關聯？但是接下來我看到了。既然兩個被移走的方格都是淺色的，那麼棋盤上剩下的是三十二個深色方格和三十個淺色方格。但因為每一張骨牌都會剛剛好涵蓋一個淺色方格和一個深色方格，所以三十一張骨牌就不可能鋪滿這樣的棋盤。這真是太酷了！

悄悄話

如果你喜歡上述最後一個證明，那我相信你也會欣賞下面這一個。電玩遊戲「俄羅斯方塊」中有七種不同形狀，有時候我們稱之為 I、J、L、O、Z、T 和 S。

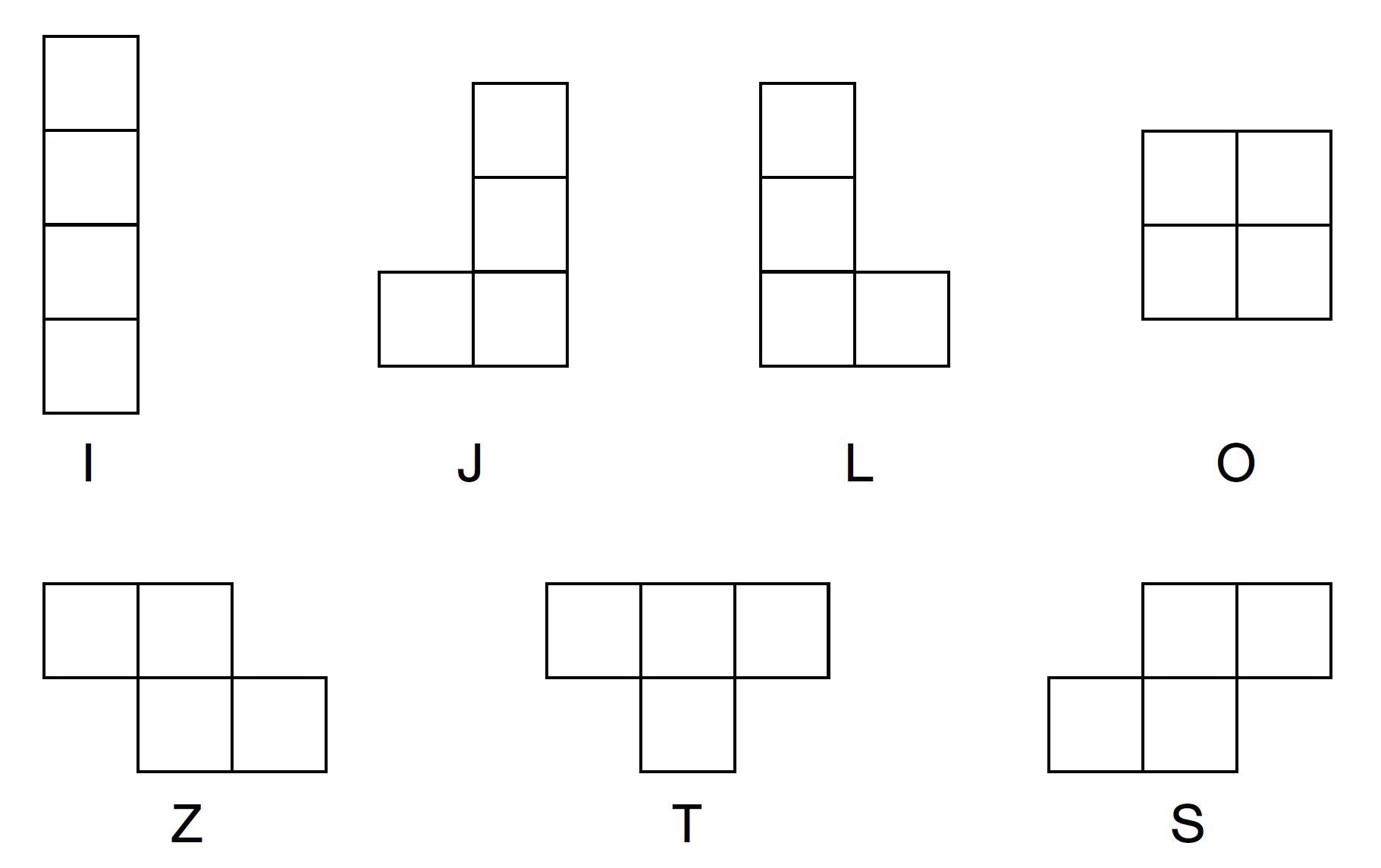這七個形狀可以排成一個四乘七的長方形嗎？圖／數學大觀念

這七個形狀可以排成一個四乘七的長方形嗎？

每一個形狀都剛好占據四個方格，所以我們自然會猜想，這七個形狀或許可以拼成一個四乘七的長方形（拼湊的過程中，我們可以翻轉或是旋轉這些形狀），但事實上這是一個不可能的任務。你要怎麼證明這是不可能的呢？讓我們將這個長方形上色，使其含有十四個淺色方格和十四個深色方格，如下圖所示。

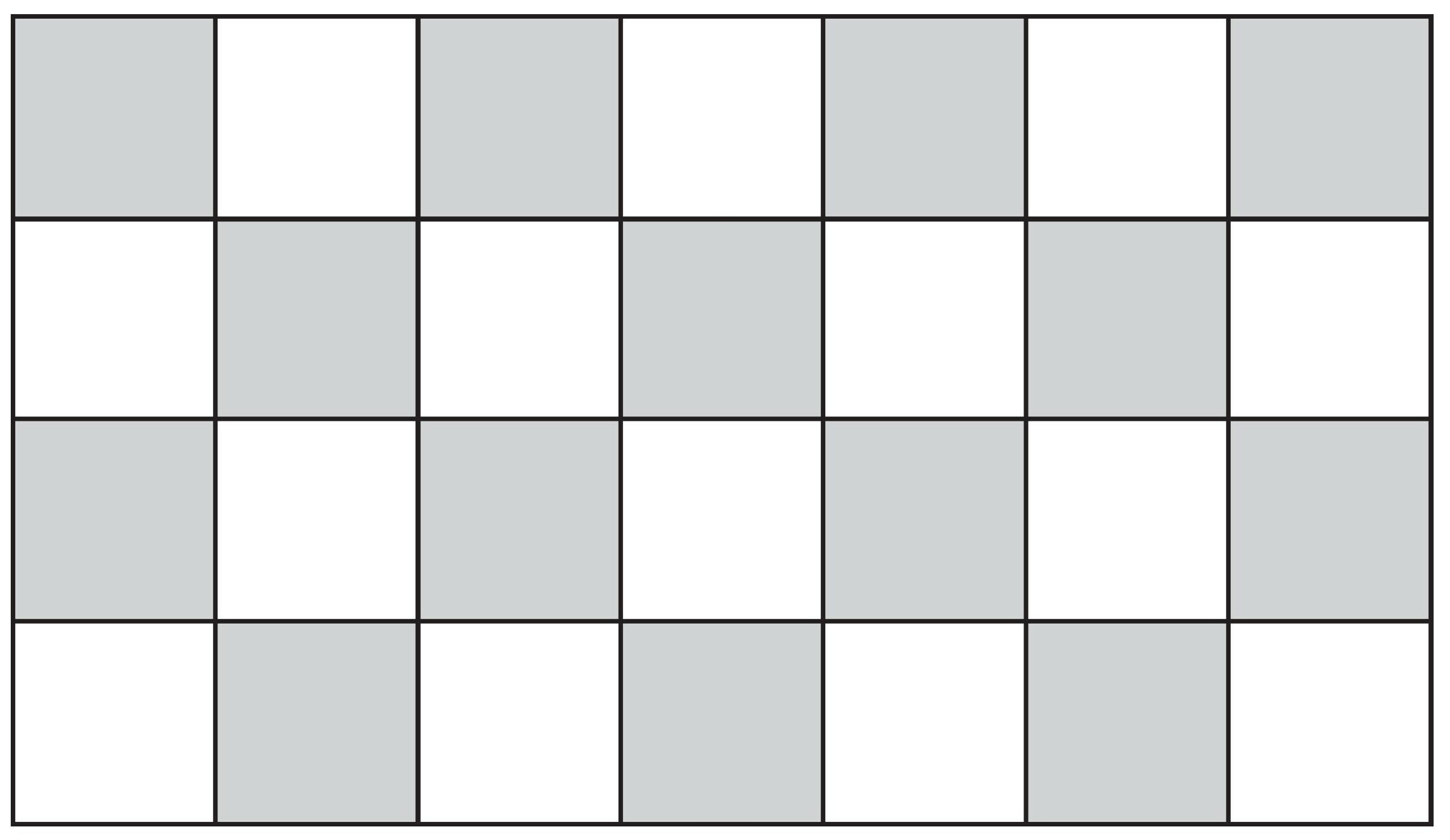
請注意，除了 T 這個形狀以外，每一個形狀不論放在棋盤的哪一個位置，都一定涵蓋兩個淺色方格和兩個深色方格。但是 T 涵蓋的範圍是三個某一種顏色的方格和一個另一種顏色的方格。於是，不論其他六個方塊放在哪裡，它們一定蓋住正好十二個淺色方格和十二個深色方格，剩下來給 T 的是兩個淺色方格和兩個深色方格，也就是這個要求不可能達成。

——本文摘自《數學大觀念：全面理解從數字到微積分的12大觀念》，2023 年 3 月，貓頭鷹出版，未經同意請勿轉載。

Read More