作者:陈恺杰,东方航空信息部,算法工程师
作者:康月馨,清华大学,清华大学深圳国际研究生院,硕士在读
修改 & 审校:刘兴禄,清华大学,清华大学深圳国际研究生院,清华-伯克利深圳学院,博士在读

-
问题描述
-
数学模型及代码实现
-
Wagner-Whitin Model
-
Shortest Path-based Formulation
-
Warehouse Location-based Formulation
数值实验
总结与展望
参考文献
批量生产问题(Lot Sizing Problem, )是生产管理、库存管理中一类常见的优化问题,旨在求解未来一段时间内的生产或订购决策,在满足需求的前提下使得总成本最小。 拥有许多不同的种类,其变种及扩展问题在现实世界中有不同的应用场景。最常见分类方式为容量是否受限(capacitated/uncapacitated)和货品种类(single-item/multi-item)。在本篇推文中,我们介绍的是最基本的容量不受限单品批量生产问题(Uncapacitated Single Item Lot Sizing Problem, ), 经常在用于求解更复杂的 算法中作为子问题出现。
并不是 难问题,Wagner and Whitin 在1958年发表于 Management Science 的论文中提出了可在多项式时间内求解该问题的动态规划算法。值得一提的是,若生产资源的容量受限,即容量受限单品批量生产问题(Capacitated Single Item Lot Sizing Problem,)则为强 难问题,可以用三分区问题(3-Partition Problem)进行为多项式归约。因为 是强 难问题,在求解大规模算例时需要借助分解算法,例如 Fix-and-Optimize,Benders 分解等等,关于 我们会在未来的推文中进行较为详细的介绍,本篇推文还是聚焦于 。
我们从 的问题描述开始,然后着重介绍三个不同的刻画 的模型及其建模思路,最后我们用Python调用COPT求解这三个模型,并对比它们的效率。
问题描述
上文提到, 是 的一种特例,仅涉及一种产品的生产决策且假设生产资源容量无限。其问题描述如下:
给定一个计划周期(planning horizon),这个计划周期由若干个离散的时间段(period)组成,每个时间段都有对应的产品市场需求量(demand),生产企业需要生产足够多的产品来满足市场需求。在生产中,需要考虑开机成本(setup cost)、单位生产成本(unit production cost)以及单位仓储成本(inventory holding host)。其中,开机成本属于固定成本(fixed cost),因为开机之后,当期可以生产任意数量的产品;而单位生产成本和单位仓储成本则属于变动成本(variable cost),因为它们由当期产量而定。不同时间段的开机成本、单位生产成本和单位仓储成本可能不同(time-varying),而生产企业则需要决策,在哪些时间段开机进行生产以及产量为多少,使得市场需求被完全覆盖,目标则为最小化总成本(开机成本+生产成本+仓储成本)。 可以用符号表示为:
-
给定
计划周期(时间段集合)
产品在时间段 的需求量
在时间段 的开机成本
在时间段 的单位生产成本
在时间段 的单位仓储成本
-
约束
每个时间段 的需求量都被满足
-
目标
最小化总成本
数学模型及代码实现
在这一节中,我们将展示三个不同的刻画 的模型以及其代码实现,其中最经典的是 Wagner and Whitin 在1958年提出的混合整数规划模型。另外, 还可以映射成最短路问题(Shortest Path Problem)和选址问题(Warehouse Location Problem)来进行建模。模型中涉及的集合和参数使用上一节中的符号,模型实现使用python语言并调用COPT 6.5求解。
Wagner-Whitin Model
Wagner-Whitin Model 也是他们于1958年提出的,它是刻画 最直观的模型,具体介绍如下:
-
变量定义
如果在时间段开机生产否则
:时间段 的生产量
:时间段 开始时的库存量
注意:在定义变量 时引入了一个虚拟的的时间段(dummy period), 的含义为时间段 开始时的库存量,实际就是时间段 结束时的库存量,即计划周期中最后一期结束后的库存量。
-
模型建立
-
模型解读
式为目标函数,最小化总成本(开机成本+生产成本+仓储成本)。
式为库存平衡约束(inventory balance equations)。
式 和式分别规定了仓库的初始(第一期)库存量和最终(最后一期)库存量为0。
式 为耦合约束,规定了若在时间段 不开机(),则当期产量为0()
注意:此式中的是一个足够大的值,可以设为。
式、式 和式 规定了决策变量的值域。
-
代码实现
def solve_wagner_whitin_model(parameter, relax=0):
# create the model
env = co.Envr()
model = env.createModel("classical_model")
# decision variables
if relax==0:
setup = model.addVars(parameter.num_periods, vtype = COPT.BINARY)
elif relax==1:
setup = model.addVars(parameter.num_periods, vtype = COPT.CONTINUOUS)
production_quantity = model.addVars(parameter.num_periods, vtype = COPT.CONTINUOUS)
inventory_quantity = model.addVars(parameter.num_periods + 1, vtype = COPT.CONTINUOUS) # inventory quantity at begin of period t# objective function
model.setObjective(co.quicksum(parameter.setup_cost[t]*setup[t] + parameter.production_cost[t]*production_quantity[t] + parameter.inventory_cost[t]*inventory_quantity[t+1] for t in range(parameter.num_periods)), COPT.MINIMIZE)# inventory balance
model.addConstrs(inventory_quantity[t+1] == inventory_quantity[t] + production_quantity[t] – parameter.demand[t] for t in range(parameter.num_periods))# initial inventory
model.addConstr(inventory_quantity[0] == 0)# end inventory
model.addConstr(inventory_quantity[parameter.num_periods] == 0)# cuts
model.addConstrs(production_quantity[t] <= parameter.demand[t:parameter.num_periods+1].sum() * setup[t] for t in range(parameter.num_periods))
# parameter of the model
model.setParam(COPT.Param.Logging, 0)model.solve()
# print solution
print(f”solving time: {model.SolvingTime}“)
if relax == 0:
print(f”total cost: {model.BestObj}“)
elif relax == 1:
print(f”total cost: {model.LpObjval}“)
print(‘=’*15)
for t in range(parameter.num_periods):
if setup[t].X == 1:
print(f”production takes place in period {t}“)
print(f”production quantity: {production_quantity[t].X}“)
print(“=”*10)
在 Wagner and Whitin 于1958年发表的论文中,对于 提出了 Zero-Inventory-Property:
必定存在一个最优解,对于每个时间段 都有 。
用文字表达就是,如果在时间段 开始时的库存量不为0,那么在该时间段就不开机生产。这意味着, 必定存在一个最优解,在这个最优解中,如果 ,那么就有 。也就是说,如果在时间段 开机进行生产的话,那么生产量为从时间段 到 时间段 (共 个连续时间段)的需求量之和。 这是 非常重要的性质,基于此,其他学者设计了其他刻画该问题的模型,下面我们就具体来看一下。
Shortest Path-based Formulation
Evans 提出用有向无环图来刻画 ,然后通过求解最短路问题(Shortest Path Problem, )来求解 。在图中,一个结点(node)代表一个时间段,共有 个时间段(存在一个虚拟时间段)。从结点 到结点 的弧代表在时间段 生产从时间段 到 时间段 的所有需求量。求解 等价于求解从结点 到结点 的最短路径。我们可以结合下图来理解:
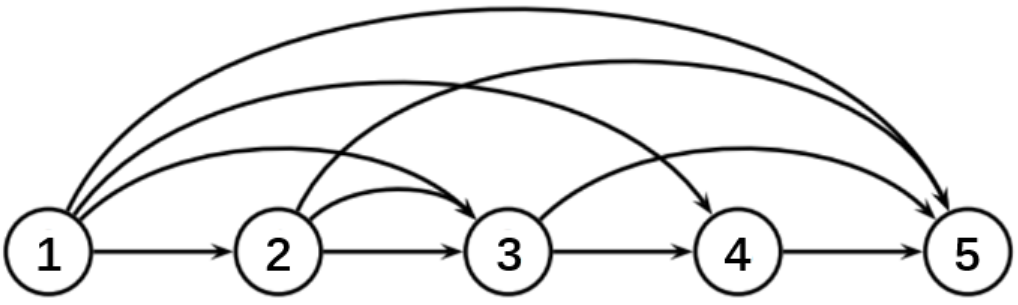
图中的5个结点代表五个时间段(),其中结点 为虚拟时间段。弧的数量为,此处 ,所以图中有10条弧。图中的每条弧代表一个生产选项(production option),例如弧表示在时间段 开机生产且生产量为时间段 到时间段 的需求量之和。 现在图中没有弧值,这里的弧值其实是生产选项对应的成本,关于弧值的计算方式马上会讲到。我们需要做的就是找到一条从结点 到结点 的最短路径,从最短路径中可以推出计划周期内总成本最低的生产方案。令 为在时间段 生产 件产品的变动成本(生产成本+仓储成本)之和,则有弧值的计算方式如下:
根据上式计算出参数 的值之后,就可以开始建立模型了:
-
变量定义
如果在时间段开机生产否则如果在时间段进行生产覆盖从时间段到时间段的需求否则
-
模型建立
-
模型解读
式为目标函数,最小化总成本(固定成本+变动成本)。
式规定,结点 有且只有一个后继结点。
式为流平衡约束(flow balance equations)。
式规定,如果在时间段 没有开机生产,则结点 没有后继结点。
式和式 规定了决策变量的值域。
-
代码实现
def solve_SPP_model_1(parameter, relax=0):
# create the model
env = co.Envr()
model = env.createModel("SPP_model_1")
# decision variables
if relax == 0:
setup = model.addVars(parameter.num_periods, vtype = COPT.BINARY)
elif relax == 1:
setup = model.addVars(parameter.num_periods, vtype = COPT.CONTINUOUS)
l = [(t,tau) for t in range(parameter.num_periods) for tau in range(t+1, parameter.num_periods+1)]
deploy_production = model.addVars(l, vtype = COPT.CONTINUOUS)# define objective function
obj1 = co.LinExpr(0)
for t in range(parameter.num_periods):
for q in range(t + 1, parameter.num_periods + 1):
d_tq = 0
for i in range(t, q):
d_tq += parameter.demand[i]
v_ti = d_tq * parameter.production_cost[t]
inventorySum = 0
for j in range(q – 1, t, -1):
inventorySum += parameter.demand[j]
v_ti += parameter.inventory_cost[j – 1] * inventorySum
obj1.addTerms(deploy_production[t, q], v_ti)
obj2 = co.LinExpr(0)
for t in range(parameter.num_periods):
obj2.addTerms(setup[t], parameter.setup_cost[t])
model.setObjective(obj1 + obj2, COPT.MINIMIZE)# quelle node
model.addConstr(co.quicksum(deploy_production[0,tau] for tau in range(1, parameter.num_periods+1)) == 1)
# flow conversation
model.addConstrs(co.quicksum(deploy_production[i,t] for i in range(t)) == co.quicksum(deploy_production[t,i] for i in range(t+1,parameter.num_periods+1)) for t in range(1,parameter.num_periods))# coping constraints
model.addConstrs(co.quicksum(deploy_production[t,i] for i in range(t+1,parameter.num_periods+1)) <= setup[t] for t in range(parameter.num_periods))# parameter of the model
model.setParam(COPT.Param.Logging, 0)model.solve()
# print solution
print(f”solving time: {model.SolvingTime}“)
if relax == 0:
print(f”total cost: {model.BestObj}“)
elif relax == 1:
print(f”total cost: {model.LpObjval}“)
print(‘=’*15)
for t in range(parameter.num_periods):
if setup[t].X > 0.99:
print(f”Production takes place in period {t}“)
for tau in range(t+1, parameter.num_periods+1):
if deploy_production[t,tau].X > 0.99:
for tt in range(t, tau):
print(f”production quantity for period {tt}: {parameter.demand[tt]}“)
print(f”=”*10) -
模型改良
在计算弧值时,我们可以把固定成本也一并纳入。令 为在时间段 生产 件产品的总成本(开机成本+生产成本+仓储成本),则有新的弧值的计算方式如下:
相应地,在模型中我们不再需要变量 以及约束,新的模型具体如下:
非常重要的是,经过改良之后,上述模型的约束矩阵为相应的有向无环图的关联矩阵,由其全单模性可知,求解该模型的线性松弛可得最优整数解,这一点我们会在数值实验一节中进行验证。
-
改良模型代码实现
def solve_SPP_model_2(parameter, relax=0):
# create the model
env = co.Envr()
model = env.createModel("SPP_model_2")
# decision variables
l = [(t,tau) for t in range(parameter.num_periods) for tau in range(t+1, parameter.num_periods+1)]
if relax==0:
deploy_production = model.addVars(l, vtype = COPT.BINARY)
elif relax==1:
deploy_production = model.addVars(l, vtype = COPT.CONTINUOUS)# define objective function
obj = co.LinExpr(0)
for t in range(parameter.num_periods):
for q in range(t + 1, parameter.num_periods + 1):
d_tq = 0
for i in range(t, q):
d_tq += parameter.demand[i]
v_ti = parameter.setup_cost[t] + d_tq * parameter.production_cost[t]
inventorySum = 0
for j in range(q – 1, t, -1):
inventorySum += parameter.demand[j]
v_ti += parameter.inventory_cost[j – 1] * inventorySum
obj.addTerms(deploy_production[t, q], v_ti)
model.setObjective(obj, COPT.MINIMIZE)# quelle node
model.addConstr(co.quicksum(deploy_production[0,tau] for tau in range(1, parameter.num_periods+1)) == 1)
# flow conversation
model.addConstrs(co.quicksum(deploy_production[i,t] for i in range(t)) == co.quicksum(deploy_production[t,i] for i in range(t+1,parameter.num_periods+1)) for t in range(1,parameter.num_periods))# parameter of the model
model.setParam(COPT.Param.Logging, 0)model.solve()
# print solution
print(f”solving time: {model.SolvingTime}“)
if relax == 0:
print(f”total cost: {model.BestObj}“)
elif relax == 1:
print(f”total cost: {model.LpObjval}“)
print(‘=’*15)
for t in range(parameter.num_periods):
for tau in range(t+1, parameter.num_periods+1):
if deploy_production[t,tau].X > 0.99:
print(f”Production takes place in period {t}“)
for tt in range(t, tau):
print(f”production quantity for period {tt}: {parameter.demand[tt]}“)
print(f”=”*10)
Warehouse Location-based Formulation
Krarup and Bilde 提出可以用选址问题(Warehouse Location Problem, )的形式对 进行建模。在这种建模思路中, 与 的映射关系如下:
WLP
USILSP
仓库时间段客户后续时间段开仓成本固定成本(开机成本)运输成本变动成本(生产成本+仓储成本)
下图可以帮我们更好地理解仓库、客户与时间段的映射关系:
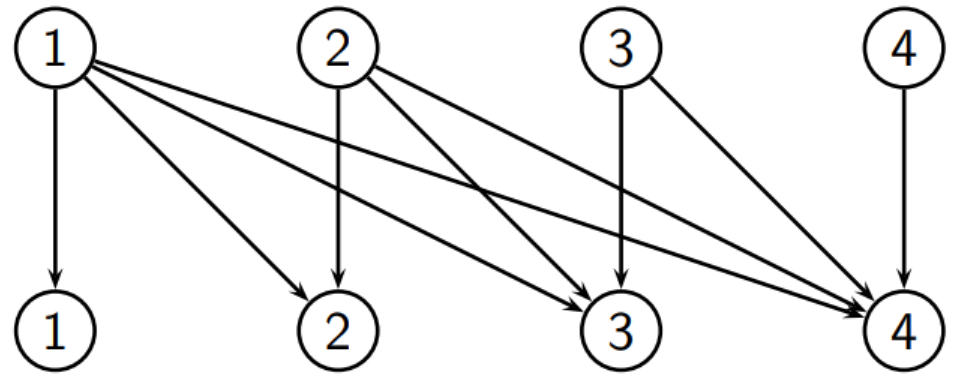
图中第一行为仓库(时间段),第二行为客户(后续时间段)。可以看到仓库 可以服务所有客户,这是因为所有时间段都是时间段 的后续时间段,而仓库 只能服务客户 、客户 以及客户 ,因为时间段 不属于时间段 的后续时间段。
在 Warehouse Location-based Formulation 中,我们需要计算在时间段 为后续时间段 进行生产所产生的单位变动成本 ,具体计算方式如下:
基于 建立的模型如下:
-
变量定义
如果在时间段开机生产否则
:在时间段 后续时间段 所生产的产品数量
-
模型建立
-
模型解读
式为目标函数,最小化总成本(固定成本+变动成本)。
式为需求覆盖约束。
式为耦合约束,规定了若在时间段 不开机,则不能为任何后续时间段 提供产品。
式和式 规定了决策变量的值域。
-
代码实现
def solve_WLP_model(parameter,relax=0):
# create the model
env = co.Envr()
model = env.createModel("WLP_model")
# processing data (save in dictionary)
cost = {(t,tau):parameter.production_cost[t]+parameter.inventory_cost[t:tau].sum() for t in range(parameter.num_periods) for tau in range(t, parameter.num_periods)}# decision variables
if relax==0:
setup = model.addVars(parameter.num_periods, vtype = COPT.BINARY)
elif relax==1:
setup = model.addVars(parameter.num_periods, vtype = COPT.CONTINUOUS)
l = [(t,tau) for t in range(parameter.num_periods) for tau in range(t, parameter.num_periods)]
production_quantity = model.addVars(l, vtype = COPT.CONTINUOUS)# objective function
model.setObjective(co.quicksum(parameter.setup_cost[t]*setup[t] + co.quicksum(cost[(t,tau)]*production_quantity[t,tau] for tau in range(t, parameter.num_periods)) for t in range(parameter.num_periods)), COPT.MINIMIZE)# demand satisfaction
model.addConstrs(co.quicksum(production_quantity[t,tau] for t in range(tau+1)) == parameter.demand[tau] for tau in range(parameter.num_periods))# coping constraints
model.addConstrs(production_quantity[t,tau] <= parameter.demand[tau]*setup[t] for t in range(parameter.num_periods) for tau in range(t, parameter.num_periods))
# parameter of the model
model.setParam(COPT.Param.Logging, 0)model.solve()
# print solution
print(f”solving time: {model.SolvingTime}“)
if relax == 0:
print(f”total cost: {model.BestObj}“)
elif relax == 1:
print(f”total cost: {model.LpObjval}“)
print(‘=’*15)
for t in range(parameter.num_periods):
if setup[t].X > 0.99:
print(f”Production takes place in period {t}“)
for tau in range(t, parameter.num_periods):
if production_quantity[t,tau].X > 0:
print(f”production quantity for period {tau}: {production_quantity[t,tau].X}“)
print(f”=”*10)
与传统的 Wagner-Whitin Model 相比,Warehouse Location-based Formulation 在于它的线性松弛的最优解与最优整数解一致,Krarup and Bilde 在论文中也证明了这一点,感兴趣的同学可以参考文末的 reference, 在数值实验中我们会对其进行验证。
数值实验
在数值实验中,我们准备了5个规模为 的算例,分别使用上文介绍的模型来求解,模型线性松弛的最优解也在下表中记录:
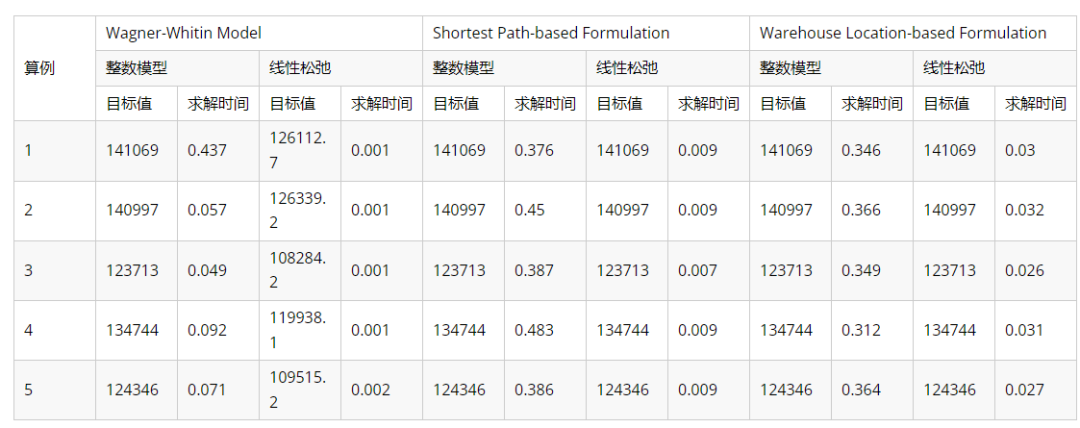
图:数值实验结果
从上表中可以看到,与传统的 Wagner-Whitin Model 相比,Shortest Path-based Formulation 和 Warehouse Location-based Formulation 的优势在于,后两者的线性松弛最优解与整数最优解相同,而求解线性松弛是相对较快的。
为了保证推文的紧凑性,我们在推文中省去了读取数据等其他部分的代码。需要测试算例和完整代码的小伙伴,可以通过下面的方式获取完整代码。大家可以尝试不同的算例进行数值实验,用来验证推文中的结论。
转发该推文至朋友圈,集齐30赞,并将集赞截图发送至公众号后台,即可免费获得。
注意,发送截图到后台时,需要提供姓名、学校、电话以及邮箱,小编将在2天之后,统一将代码发送给各位小伙伴。2天之内不发送,望各位读者周知。
总结与展望
本片推文重点介绍了 ,该问题并不是 难问题,可以用动态规划在多项式时间内精确求解,从数值实验的结果也可以看到,通过建模调用 solver 求解也并不耗时。我们介绍了三种不同的建模方式,其中 Shortest Path-based Formulation 和 Warehouse Location-based Formulation 的线性松弛最优解与整数最优解是相同的,这个特点为求解提供了极大的便利。
的实际应用场景并不多,因为在现实中,几乎不存在生产资源容量不受限的情况。但这并不意味着 不重要,因为它经常作为更复杂变种 的子问题在算法中出现。 若资源容量受限,即使只生产一类产品,问题的复杂度也是强 难。在未来的推文中,我们计划介绍容量受限的多品批量生产问题(Capacitated Multi Item Lot Sizing Problem,)及其求解方法,尽情期待。
参考文献
- Brahimi N,Dauzere-Peres S,Najid M N, et al. Single item lot sizing problems[J]. European Journal of Operational Research,2004,168(1)
- J.R. Evans, An efficient implementation of the Wagner– Whitin algorithm for dynamic lot-sizing, Journal of Operations Management 5 (2) (1985) 229–235
- J. Krarup, O. Bilde, Plant location, set covering and economic lot size: An O(mn)-algorithm for structured problems, in: International Series of Numerical Mathematics, vol. 36, Birkhaeuser Verlag, 1977, pp. 155–1
- H.M. Wagner, T.M. Whitin, Dynamic version of the economic lot size model, Management Science 5 (1) (1958) 89–96
微信公众号后台回复
加群:加入全球华人OR|AI|DS社区硕博微信学术群
资料:免费获得大量运筹学相关学习资料
人才库:加入运筹精英人才库,获得独家职位推荐
电子书:免费获取平台小编独家创作的优化理论、运筹实践和数据科学电子书,持续更新中ing…
加入我们:加入「运筹OR帷幄」,参与内容创作平台运营
知识星球:加入「运筹OR帷幄」数据算法社区,免费参与每周「领读计划」、「行业inTalk」、「OR会客厅」等直播活动,与数百位签约大V进行在线交流

文章须知
文章作者:运小筹
责任编辑:Road Rash
微信编辑:疑疑
文章由『运筹OR帷幄』转载发布
如需转载请在公众号后台获取转载须知
关注我们
FOLLOW US







 ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง
ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง


