【智能优化算法】基于拔河优化算法求解单目标优化问题附matlab代码

✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，matlab项目合作可私信。

🍎个人主页：Matlab科研工作室

🍊个人信条：格物致知。

更多Matlab完整代码及仿真定制内容点击👇

智能优化算法       神经网络预测       雷达通信      无线传感器        电力系统

信号处理              图像处理               路径规划       元胞自动机        无人机

❤️ 内容介绍

在当今信息时代，优化问题已经成为了各个领域中不可或缺的一部分。从工程设计到金融投资，从交通规划到机器学习，优化问题的解决对于提高效率、降低成本和优化资源利用至关重要。为了解决这些问题，人们开发了各种各样的优化算法，其中之一就是拔河优化算法。

拔河优化算法最初是受到人类拔河比赛的启发而提出的。在拔河比赛中，两个队伍通过拉绳子的方式进行比拼，目标是将对方队伍拉到自己一侧。这个过程中，队伍成员需要通过协作和合理分配力量来实现最佳的结果。基于这个思想，拔河优化算法将问题的解决过程看作是一个协作的过程，通过不断调整个体的位置来达到最优解。

拔河优化算法的基本原理是通过模拟队伍成员的行为来求解问题。首先，算法初始化一组随机解作为初始队伍位置。然后，通过计算每个个体与目标的适应度值来评估其位置的好坏。适应度值可以根据问题的具体情况进行定义，例如在工程设计中可以是成本、效率或者质量指标。接下来，算法根据适应度值来调整每个个体的位置，模拟队伍成员的行为。这个过程中，个体之间可以通过合作和竞争来调整位置，以达到更好的结果。最后，算法根据设定的终止条件判断是否终止，并返回最优解。

拔河优化算法具有一些独特的优点。首先，它是一种全局优化算法，能够在整个搜索空间中寻找最优解。其次，它具有较强的鲁棒性，能够应对复杂的问题和噪声干扰。此外，拔河优化算法还可以与其他优化算法相结合，形成混合算法，进一步提高求解效果。

然而，拔河优化算法也存在一些不足之处。首先，算法的收敛速度较慢，特别是在高维问题中。其次，算法对于问题的可行域边界不敏感，容易陷入局部最优解。此外，算法的参数设置对于算法性能的影响较大，需要经验性的调整。

为了应对这些问题，研究者们提出了许多改进的拔河优化算法。例如，引入了自适应策略来调整算法的参数，提高算法的性能。另外，结合其他优化算法的思想，如遗传算法和粒子群算法，形成混合算法，能够充分利用各自的优点，提高求解效果。

总结起来，拔河优化算法是一种基于协作和合作的智能优化算法，能够应对各种单目标优化问题。虽然算法存在一些不足之处，但通过改进和优化，可以进一步提高算法的性能。随着信息技术的不断发展，拔河优化算法有望在各个领域中得到更广泛的应用，并为问题的解决提供更好的方法和思路。

🔥核心代码



function [lowerbound,upperbound,dimension,fitness] = fun_info(F)

switch F case 'F1' fitness = @F1; lowerbound=-100; upperbound=100; dimension=30; case 'F2' fitness = @F2; lowerbound=-10; upperbound=10; dimension=30; case 'F3' fitness = @F3; lowerbound=-100; upperbound=100; dimension=30; case 'F4' fitness = @F4; lowerbound=-100; upperbound=100; dimension=30; case 'F5' fitness = @F5; lowerbound=-30; upperbound=30; dimension=30; case 'F6' fitness = @F6; lowerbound=-100; upperbound=100; dimension=30; case 'F7' fitness = @F7; lowerbound=-1.28; upperbound=1.28; dimension=30; case 'F8' fitness = @F8; lowerbound=-500; upperbound=500; dimension=30; case 'F9' fitness = @F9; lowerbound=-5.12; upperbound=5.12; dimension=30; case 'F10' fitness = @F10; lowerbound=-32; upperbound=32; dimension=30; case 'F11' fitness = @F11; lowerbound=-600; upperbound=600; dimension=30; case 'F12' fitness = @F12; lowerbound=-50; upperbound=50; dimension=30; case 'F13' fitness = @F13; lowerbound=-50; upperbound=50; dimension=30; case 'F14' fitness = @F14; lowerbound=-65.536; upperbound=65.536; dimension=2; case 'F15' fitness = @F15; lowerbound=-5; upperbound=5; dimension=4; case 'F16' fitness = @F16; lowerbound=-5; upperbound=5; dimension=2; case 'F17' fitness = @F17; lowerbound=[-5,0]; upperbound=[10,15]; dimension=2; case 'F18' fitness = @F18; lowerbound=-2; upperbound=2; dimension=2; case 'F19' fitness = @F19; lowerbound=0; upperbound=1; dimension=3; case 'F20' fitness = @F20; lowerbound=0; upperbound=1; dimension=6; case 'F21' fitness = @F21; lowerbound=0; upperbound=10; dimension=4; case 'F22' fitness = @F22; lowerbound=0; upperbound=10; dimension=4; case 'F23' fitness = @F23; lowerbound=0; upperbound=10; dimension=4; end
end
% F1
function R = F1(x)R=sum(x.^2);end
% F2
function R = F2(x)R=sum(abs(x))+prod(abs(x));end
% F3
function R = F3(x)dimension=size(x,2);R=0;for i=1:dimension R=R+sum(x(1:i))^2;endend
% F4
function R = F4(x)R=max(abs(x));end
% F5
function R = F5(x)dimension=size(x,2);R=sum(100*(x(2:dimension)-(x(1:dimension-1).^2)).^2+(x(1:dimension-1)-1).^2);end
% F6
function R = F6(x)R=sum(abs((x+.5)).^2);end
% F7
function R = F7(x)dimension=size(x,2);R=sum([1:dimension].*(x.^4))+rand;end
% F8
function R = F8(x)R=sum(-x.*sin(sqrt(abs(x))));end
% F9
function R = F9(x)dimension=size(x,2);R=sum(x.^2-10*cos(2*pi.*x))+10*dimension;end
% F10
function R = F10(x)dimension=size(x,2);R=-20*exp(-.2*sqrt(sum(x.^2)/dimension))-exp(sum(cos(2*pi.*x))/dimension)+20+exp(1);end
% F11
function R = F11(x)dimension=size(x,2);R=sum(x.^2)/4000-prod(cos(x./sqrt([1:dimension])))+1;end
% F12
function R = F12(x)dimension=size(x,2);R=(pi/dimension)*(10*((sin(pi*(1+(x(1)+1)/4)))^2)+sum((((x(1:dimension-1)+1)./4).^2).*...(1+10.*((sin(pi.*(1+(x(2:dimension)+1)./4)))).^2))+((x(dimension)+1)/4)^2)+sum(Ufun(x,10,100,4));end
% F13
function R = F13(x)dimension=size(x,2);R=.1*((sin(3*pi*x(1)))^2+sum((x(1:dimension-1)-1).^2.*(1+(sin(3.*pi.*x(2:dimension))).^2))+...((x(dimension)-1)^2)*(1+(sin(2*pi*x(dimension)))^2))+sum(Ufun(x,5,100,4));end
% F14
function R = F14(x)aS=[-32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32;,...-32 -32 -32 -32 -32 -16 -16 -16 -16 -16 0 0 0 0 0 16 16 16 16 16 32 32 32 32 32];
for j=1:25 bS(j)=sum((x'-aS(:,j)).^6);endR=(1/500+sum(1./([1:25]+bS))).^(-1);end
% F15
function R = F15(x)aK=[.1957 .1947 .1735 .16 .0844 .0627 .0456 .0342 .0323 .0235 .0246];bK=[.25 .5 1 2 4 6 8 10 12 14 16];bK=1./bK;R=sum((aK-((x(1).*(bK.^2+x(2).*bK))./(bK.^2+x(3).*bK+x(4)))).^2);end
% F16
function R = F16(x)R=4*(x(1)^2)-2.1*(x(1)^4)+(x(1)^6)/3+x(1)*x(2)-4*(x(2)^2)+4*(x(2)^4);end
% F17
function R = F17(x)R=(x(2)-(x(1)^2)*5.1/(4*(pi^2))+5/pi*x(1)-6)^2+10*(1-1/(8*pi))*cos(x(1))+10;end
% F18
function R = F18(x)R=(1+(x(1)+x(2)+1)^2*(19-14*x(1)+3*(x(1)^2)-14*x(2)+6*x(1)*x(2)+3*x(2)^2))*... (30+(2*x(1)-3*x(2))^2*(18-32*x(1)+12*(x(1)^2)+48*x(2)-36*x(1)*x(2)+27*(x(2)^2)));end
% F19
function R = F19(x)aH=[3 10 30;.1 10 35;3 10 30;.1 10 35];cH=[1 1.2 3 3.2];pH=[.3689 .117 .2673;.4699 .4387 .747;.1091 .8732 .5547;.03815 .5743 .8828];R=0;for i=1:4 R=R-cH(i)*exp(-(sum(aH(i,:).*((x-pH(i,:)).^2))));endend
% F20
function R = F20(x)aH=[10 3 17 3.5 1.7 8;.05 10 17 .1 8 14;3 3.5 1.7 10 17 8;17 8 .05 10 .1 14];cH=[1 1.2 3 3.2];pH=[.1312 .1696 .5569 .0124 .8283 .5886;.2329 .4135 .8307 .3736 .1004 .9991;....2348 .1415 .3522 .2883 .3047 .6650;.4047 .8828 .8732 .5743 .1091 .0381];R=0;for i=1:4 R=R-cH(i)*exp(-(sum(aH(i,:).*((x-pH(i,:)).^2))));endend
% F21
function R = F21(x)aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];
R=0;for i=1:5 R=R-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);endend
% F22
function R = F22(x)aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];
R=0;for i=1:7 R=R-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);endend
% F23
function R = F23(x)aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];
R=0;for i=1:10 R=R-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);endend
function R=Ufun(x,a,k,m)R=k.*((x-a).^m).*(x>a)+k.*((-x-a).^m).*(x<(-a));end




❤️ 运行结果

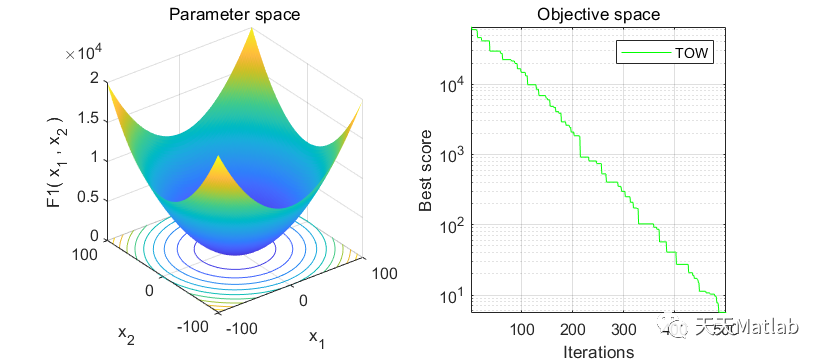
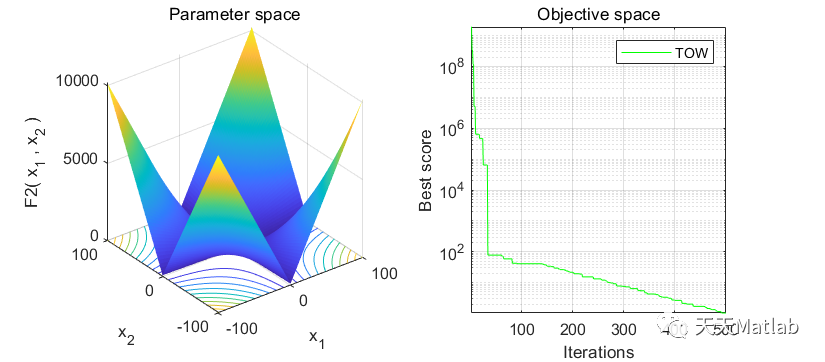
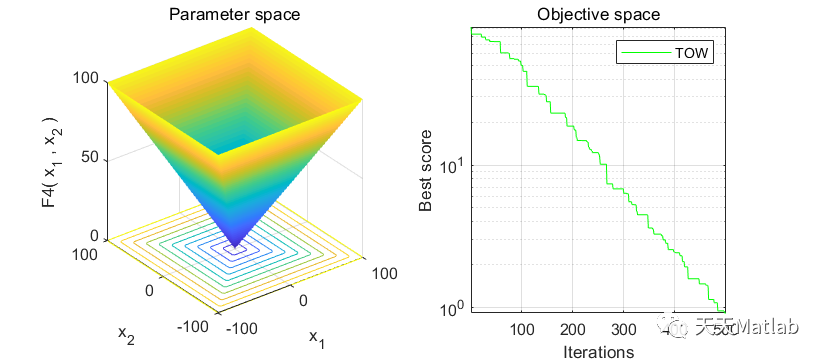
⛄ 参考文献

❤️部分理论引用网络文献，若有侵权联系博主删除

❤️ 关注我领取海量matlab电子书和数学建模资料

🍅 私信完整代码和数据获取及论文数模仿真定制

1 各类智能优化算法改进及应用

生产调度、经济调度、装配线调度、充电优化、车间调度、发车优化、水库调度、三维装箱、物流选址、货位优化、公交排班优化、充电桩布局优化、车间布局优化、集装箱船配载优化、水泵组合优化、解医疗资源分配优化、设施布局优化、可视域基站和无人机选址优化

2 机器学习和深度学习方面

卷积神经网络（CNN）、LSTM、支持向量机（SVM）、最小二乘支持向量机（LSSVM）、极限学习机（ELM）、核极限学习机（KELM）、BP、RBF、宽度学习、DBN、RF、RBF、DELM、XGBOOST、TCN实现风电预测、光伏预测、电池寿命预测、辐射源识别、交通流预测、负荷预测、股价预测、PM2.5浓度预测、电池健康状态预测、水体光学参数反演、NLOS信号识别、地铁停车精准预测、变压器故障诊断

2.图像处理方面

图像识别、图像分割、图像检测、图像隐藏、图像配准、图像拼接、图像融合、图像增强、图像压缩感知

3 路径规划方面

旅行商问题（TSP）、车辆路径问题（VRP、MVRP、CVRP、VRPTW等）、无人机三维路径规划、无人机协同、无人机编队、机器人路径规划、栅格地图路径规划、多式联运运输问题、车辆协同无人机路径规划、天线线性阵列分布优化、车间布局优化

4 无人机应用方面

无人机路径规划、无人机控制、无人机编队、无人机协同、无人机任务分配

、无人机安全通信轨迹在线优化

5 无线传感器定位及布局方面

传感器部署优化、通信协议优化、路由优化、目标定位优化、Dv-Hop定位优化、Leach协议优化、WSN覆盖优化、组播优化、RSSI定位优化

6 信号处理方面

信号识别、信号加密、信号去噪、信号增强、雷达信号处理、信号水印嵌入提取、肌电信号、脑电信号、信号配时优化

7 电力系统方面

微电网优化、无功优化、配电网重构、储能配置

8 元胞自动机方面

交通流 人群疏散 病毒扩散 晶体生长 火灾扩散

9 雷达方面

卡尔曼滤波跟踪、航迹关联、航迹融合、状态估计