
导语
如何量化不同复杂网络之间的相似性或差异度?这是发展关于复杂网络的统计物理理论的必要基础。近日发表于 Physical Review Research 的一项最新研究提出了一种为复杂网络建立系综的理论,来解析计算任意两个网络间的相似或差异度。本周的因果涌现读书会将由论文一作、清华大学心理学系&脑与智能实验室研究生田洋详细解读这篇论文。
「因果涌现」系列读书会第三季由北京师范大学教授、集智俱乐部创始人张江领衔发起,组织对本话题感兴趣的朋友,深入探讨因果涌现的核心理论,详细梳理领域发展脉络,并发掘因果涌现在生物网络和脑网络、涌现探测等方面的应用。读书会自7月11日开始,每周二晚19:00-21:00直播,预计持续时间10周。读书会分享在持续招募中,欢迎感兴趣的朋友报名参与!

分享内容简介
网络比较(Network comparison)旨在解析地度量复杂网络间的相似或差异度,这既是许多机器学习任务的前置条件,也是发展关于复杂网络的统计物理理论的必要基础。已有的技术通常采用数据驱动的方式来度量网络关系,但这些方法不适用于物理学的解析推导,也常囿于计算复杂度和泛化性方面的局限。
为了解决这一问题,来自清华大学脑与智能实验室、伦敦大学学院 (UCL)计算机系、法国 Université Paris-Saclay 数学中心和华为2012实验室的联合研究团队进行了一项理论研究 [1]。该研究提出了一种为复杂网络建立系综的理论,使得每个给定拓扑、动力学的网络都对应着一个唯一确定的随机变量。通过定义随机变量间的信息(如编码、解码)或因果关系 (Granger 因果性和条件互信息),研究者能解析计算任意两个网络间的相似或差异度。这一框架不仅规避了网络比较领域常见的 NP hard 问题,还为建立复杂网络的统计物理分析提供了理论推导基础。
在本次分享中,论文第一作者田洋将从研究背景、挑战和新发现等多个视角为网络比较领域提供深入和系统的介绍。
内容大纲
-
网络比较(Network comparison)的定义、价值和挑战
-
基础概念
-
应用样例
-
已有理论及其局限
网络比较(Network comparison)的定义、价值和挑战
基础概念
应用样例
已有理论及其局限
一种用于网络比较的概率方法
-
建立网络比较的概率方法的动机
-
数学原理概述和核心结果
-
计算实验与分析
-
随机图演化
-
复杂网络最优嵌入与查询
核心概念
-
网络比较 Network comparison
-
编码/解码 Encoding/Decoding
-
因果性 Causality
-
拉普拉斯算子 Laplacian
- 系综 Ensemble
网络比较 Network comparison
编码/解码 Encoding/Decoding
因果性 Causality
拉普拉斯算子 Laplacian
主讲人简介
 田洋,清华大学心理学系&脑与智能实验室研究生,研究方向是复杂系统的统计物理原理。
田洋,清华大学心理学系&脑与智能实验室研究生,研究方向是复杂系统的统计物理原理。
学者主页:https://pattern.swarma.org/user/53894
论文简介
 论文题目:Network comparison via encoding, decoding, and causality论文地址:https://journals.aps.org/prresearch/abstract/10.1103/PhysRevResearch.5.033129
论文题目:Network comparison via encoding, decoding, and causality论文地址:https://journals.aps.org/prresearch/abstract/10.1103/PhysRevResearch.5.033129
关键词:复杂网络,图论,统计物理,系综理论,信息论,因果
量化复杂网络之间的关系(例如相似性)为研究跨网络共享的潜在信息铺平了道路。然而,在网络之间,基本的关系度量并不是清晰定义的。作为一种折衷,普遍的技术采用数据驱动的方式来测量网络之间的关系,但这种方法在物理学的分析推导中是不适用的。为了解决这个问题,这项研究提出一种理论来获取网络拓扑性质的最佳刻画。
研究展示了一个网络可以通过 Laplacian 函数定义的高斯变量来完全表示,这个函数同时满足网络拓扑相关的平滑性和最大熵性质。基于这个理论,可以解析地测量复杂网络之间的各种关系。
作为示例,研究定义了网络之间的编码(例如信息散度和互信息)、解码(例如费舍尔信息)以及因果关系(例如 Granger 因果和条件互信息),并在代表性网络上验证了该框架(例如随机网络、蛋白质结构和化合物),以证明一系列科学和工程挑战(例如网络演化、嵌入和查询)可以从一个新的角度来解决。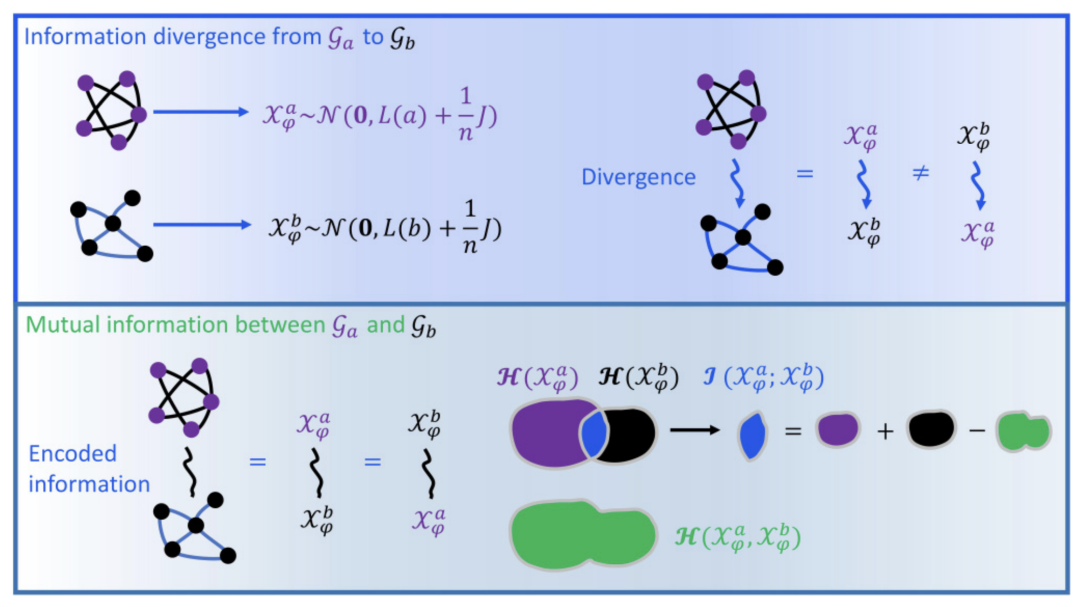 图1. 复杂网络之间的信息散度和互信息
图1. 复杂网络之间的信息散度和互信息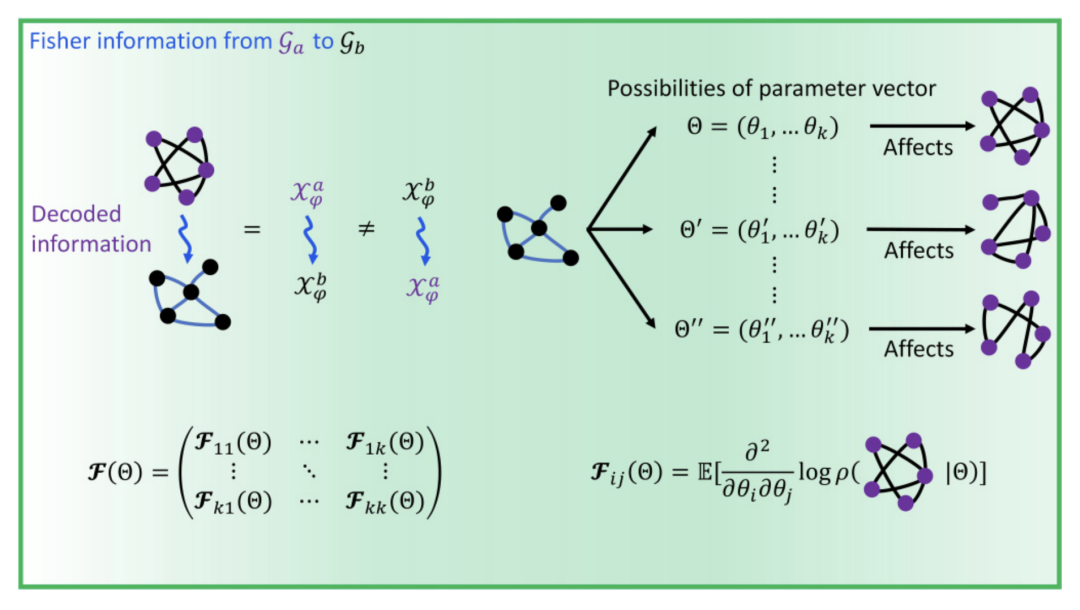 图2. 复杂网络之间的费舍尔信息
图2. 复杂网络之间的费舍尔信息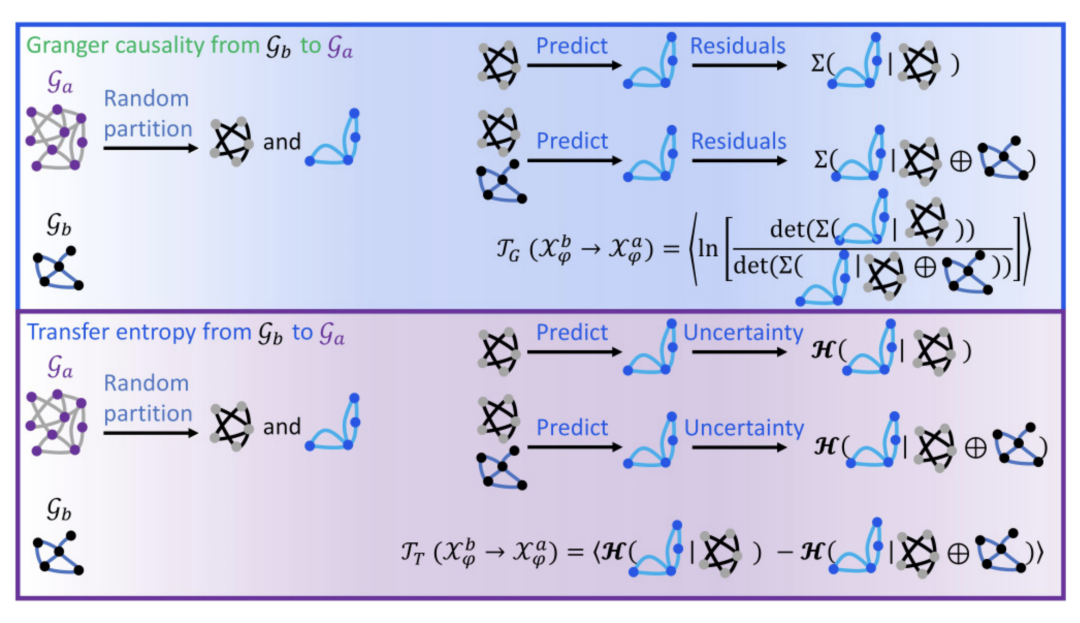 图3. 复杂网络之间的Granger 因果和条件互信息
图3. 复杂网络之间的Granger 因果和条件互信息
直播信息
时间:2023年9月12日(本周二)晚19:00-21:00
参与方式: 读书会页面:https://pattern.swarma.org/study_group_issue/519
读书会页面:https://pattern.swarma.org/study_group_issue/519
扫码参与因果涌现读书会,加入群聊,获取系列读书会回看权限,加入因果涌现社区,与社区的一线科研工作者沟通交流,共同推动因果涌现这一前沿领域的发展。
参考文献
[1] Tian, Y., Hou, H., Xu, G., Zhang, Z., & Sun, P. (2023). Network comparison via encoding, decoding, and causality. Physical Review Research, 5(3), 033129.
作者的其它相关研究
网络科学集智课堂第三期:
从数学建模到多学科应用
从现实社会的关系网到虚拟的互联网,从线下到线上,我们的生活始终没有脱离复杂网络。真实的复杂网络从其诞生开始就不断地演化着。网络节点不断地增加,节点之间的连接不断地增长。然而,复杂网络的形成机制是什么?具有什么样的演化规律?它们的演化机制对网络的功能和动力学行为有什么影响?为了回答这些问题,科学家们对复杂网络的探索从未停止。
网络科学是一个蓬勃发展的崭新交叉学科,可以看做复杂系统的骨架,核心是研究各种大型复杂网络之间的共性和处理它们的普适方法,其研究对于发展复杂系统的基本理论及构建产生了极大的推动作用。
网络科学的第三个十年,已经过去了几年。从国内外网络科学研究的发展趋势来看,各种各样的更复杂的网络模型和结构以及高阶相互作用动力学引起了人们的极大兴趣。为了回应这种迫切需求, 网络科学第三期课程围绕复杂网络的数学建模与应用进行多角度的介绍。集智学园特邀陈关荣、樊瑛、周进、李翔、张江、闫小勇、刘宗华、石川、虞文武、赵海兴、史定华加入打造第三期课程,欢迎你的加入。详情请点击:从数学建模到多学科应用——网络科学·集智课堂全新升级
因果科学读书会
集智俱乐部已经组织三季“因果科学”读书会,形成了超过千人的因果科学社区。第一季因果科学与Causal AI读书会梳理了因果科学的整体框架,形成因果科学的全局索引地图;第二季读书会进一步深入细节,从基础知识及基本技能建立因果科学的计算框架,搭建因果推理与实际研究的桥梁;在此基础上,第三季读书会致力于探究因果研究范式,真正解决多学科领域的因果问题。因果表征学习读书会是其第四季,加入任意一季读书会即可加入因果社区。
详情请见:连接因果科学与深度学习的桥梁:因果表征学习读书会启动
因果涌现读书会
跨尺度、跨层次的涌现是复杂系统研究的关键问题,生命起源和意识起源这两座仰之弥高的大山是其代表。而因果涌现理论、机器学习重整化技术、信息论或信息分解等近年来新兴的理论与工具,有望破解复杂系统的涌现规律。而新兴的因果表征学习、量子因果等领域也将为因果涌现研究注入新鲜血液。
集智俱乐部因果涌现读书会目前已经进行了两季。第一季读书会系统地梳理了因果涌现的概念,以及它与Sloopy Model、复杂性阈值、自指等概念之间的联系,也探讨了因果涌现理论在复杂网络、机器学习中的应用。参看:因果涌现读书会启动:连接因果、涌现与自指——跨尺度动力学与因果规律的探索。第二季读书会探讨了涌现、因果科学和机器学习三大主题的融合,包括信息论拓展、因果涌现理论、因果表示学习、多尺度机器学习动力学建模。参看:因果、涌现与机器学习:因果涌现读书会第二季启动。
此次因果涌现读书会第三季,将进一步围绕因果涌现的核心问题「因果涌现的定义」以及「因果涌现的辨识」进行深入学习和讨论,对 Erik Hoel 提出的 Causal Emergence,Causal Geometry 等因果涌现的核心理论进行探讨和剖析,并详细梳理其中涉及到的方法论,包括从动力学约简、隐空间动力学学习等其他领域中学习和借鉴相关的研究思路,最后探讨因果涌现的应用,包括基于生物网络、脑网络或者涌现探测等问题展开扩展,发掘更多的实际应用场景。
因果涌现社区聚集了500+成员,积累了大量论文解读资料。欢迎感兴趣的朋友报名,加入因果涌现社区,并解锁对应录播权限。
本季读书会详情与报名方式请参考:
因果涌现读书会第三季启动:深入多尺度复杂系统核心,探索因果涌现理论应用
点击“阅读原文”,报名读书会





 ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง
ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง


