
今天为大家介绍的是来自中国石油大学(华东)AITA团队在IEEE Transactions on Parallel and
Distributed Systems上发表的一篇在GPU上加速时间序列聚类的论文。
目前,时间序列分析已经应用于许多领域中,包括生物信息学、医疗,天文学、气候科学等。聚类是时间序列分析中最关键的方法之一。迄今为止,最先进的时间序列聚类算法之一是k-Shape,它不仅因为具有高精度,相对较低的计算成本而广泛应用。然而,由于时间序列数据的高异质性,因此不能简单地将其视为高维向量。两个时间序列通常需要一些对齐方法来进行相似性比较。序列之间的对齐通常是一个耗时的过程。例如,当使用动态时间规整作为序列对齐算法,并且时间序列的长度大于1000时,聚类过程中的单次迭代可能需要数百到数万秒,而整个聚类周期通常需要数十次迭代,这意味着聚类的时间成本是十分高昂的。本文提出了一组适用于GPU计算模型的并行策略,它将分析过程分为三个阶段:数据聚合、质心计算和类分配。Times-C包括了这三个阶段的高效并行算法和相应的实现。
一、引言
在数据挖掘领域中,时间序列数据是指在一系列有间隔时间点上规律的收集的观测或测量数据。许多数据格式都以时间序列数据的形式存储,例如生物学、医疗保健(血压和心电图测量)以及众多大规模科学设施,如天文学、气候科学、粒子物理学和基因组学。在应用于时间序列数据分析的所有技术中,时间序列聚类是最关键的之一,因为它不依赖于昂贵的人工监督或耗时的数据标注。通过聚类,我们可以获得将数据分割为不同的类别,并捕获原始数据的总体特征。近年来,时间序列聚类已经应用于许多领域。随着大数据技术和数据采集技术的发展,时间序列数据的规模在不断增加,因此及时高效的时间序列聚类算法变得更加重要。
近几十年来,时间序列聚类算法得到了发展。具体来说,为了有效计算不同序列之间的相似性,动态时间规整(DTW)算法已经被开发出来。该算法通过基于序列之间的距离矩阵,计算一个序列中每个点与另一个序列中多个连续点之间的相似性。通过搜索距离矩阵,可以获得对齐序列的相似性。然而,在DTW算法中,距离矩阵的生成是耗时的,因为计算的下一步依赖于上一步的结果,这会导致一个串行的工作流程,并降低并行性。
另一个常用的与领域无关的时间序列聚类算法是k-Shape算法。与基于DTW的时间序列聚类算法相比,k-Shape算法在相同精度下具有更小的计算成本,先前的研究表明,k-Shape算法实现了10倍的加速。然而,面对数据规模的激增,k-Shape算法的性能仍然受到两个非常耗时的关键阶段的限制。第一个阶段是相似性计算,该阶段必须对序列中每个时间点在时间轴上的偏移进行计算。第二个阶段是类中心提取,在该阶段中,将类中的所有数据视为单个矩阵,并将对应矩阵最大特征值所对应的特征向量用作类中心。
二、算法介绍
时间序列相似性:在大多数情况下,即使两个时间序列在整体上相似,它们的形状在时间轴上可能未对齐。因此,为了在比较相似性之前实现更好的对齐,其中一个(或两个)序列需要在时间轴上进行偏移。在时间序列聚类的相似性测量方法中,广泛应用的是动态时间规整(DTW)算法。然而,由于其高计算成本,DTW并不高效。因此,k-Shape算法使用互相关作为时间序列数据之间相似性的度量方法。
对于互相关计算,如果序列的长度为m,则需要计算2·m – 1个偏移量,每个偏移量后需要m次乘法运算,因此整个过程的时间复杂度为O(m^2)。这种计算成本是十分高昂的,但从卷积定理可以得知,时域中的互相关计算等于频域中的乘积,因此,互相关计算可以转换为快速傅里叶便变换进行加速。
时间序列质心提取:k-Shape算法将质心的提取转化为一个优化问题。对于每个类,目标是找到具有与类中所有时间序列的最大相似度的中心序列μ。为了方便起见,k-Shape算法优化了相似性的平方,即:
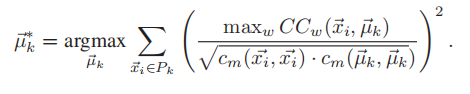
在公式中,其中符号CCw代表序列x和序列μ的互相关,而分母代表对互相关进行标准化,通过对公式进行化简,可使公式变为:
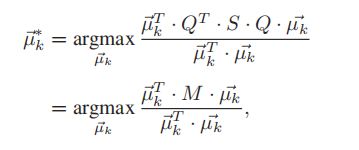
其中Q = I – (1/m)O,I是单位矩阵,O是全为1的矩阵。
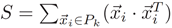
在这种情况下,优化后的目标函数被称为瑞利商最大化问题,并且被最大化的μ可以归结为实对称矩阵M的最大特征值所对应的特征向量。
k-Shape是一个迭代的优化过程,在每次迭代中,k-Shape执行两个步骤:
(i)在类中心提取步骤中,算法根据每个类中包含的数据提取出每个类的质心,即求矩阵M的最大特征值所对应的特征向量;
(ii)在分配步骤中,算法通过将每个时间序列与所有类中心进行比较,比较方式为计算时间序列与类中心的互相关。并将每个时间序列分配给最近的质心来更新成员所属的类别。
算法重复执行这两个步骤,直到类别成员关系不再改变或达到允许的最大迭代次数。在分配步骤中,k-Shape主要依赖于相似性度量,而在提取步骤中,主要依赖于质心计算方法。
然而,在处理大规模数据集时,时间序列聚类的计算并不高效。下图测试了k-Shape算法在十次迭代中单次迭代的平均执行时间。图中显示了k-Shape算法的时间成本随着数据长度、数据大小和k值的增长而增加。从图中可以看出,k-Shape算法的运行时间随着数据长度的增加呈超线性增长,随着数据大小和k值的增加呈线性增长。
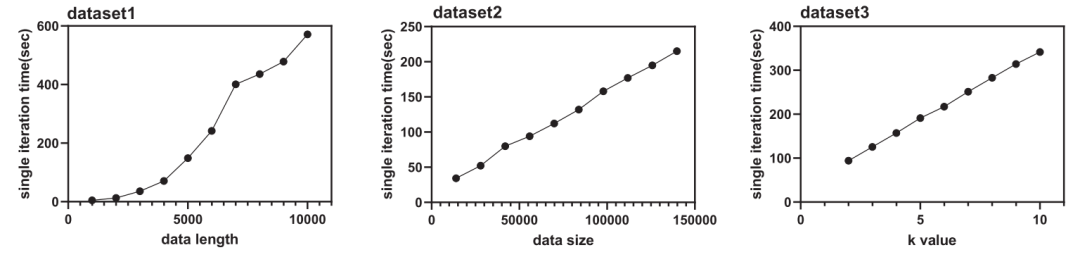
图1:不同指标下k-shape算法运行时间
当数据量增加时,k-Shape算法的单次迭代将需要数百秒的时间。如果设置了超过十次的迭代,程序可能需要几个小时,甚至可能超过十几个小时才能执行完成。现有的数据,无论是数据长度还是数据大小,都远远超过了几年前的情况。未来的数据量可能会变得更大。因此,本文从三个方面对k-Shape算法进行并行优化,以获得更好的性能。
三、优化方法
3.1、并行数据聚合
要想更新每个类的中心,必须将相同类别的数据聚合在一起。原始算法使用了最简单的两层循环遍历来聚合数据,因此其并行效率较低。更好的选择是根据类别对数据进行排序。然而,由于时间序列的高维性,以及在排序过程中每个序列需多次移动,这种改进仍然效率不高。本文设计了一种高效的哈希算法,以最小化数据移动。它由两个步骤组成。第一步是并行确定每个数据哈希的位置,第二步在每个时间点上执行并行哈希排序。
下图展示了一种获取时间序列类内偏移的串行方法,该方法需要每个时间序列的索引以及它所属的类别。这种方法将偏移索引初始化为零,并声明一个临时变量表。接下来,它按照数据所属的类别索引顺序查询表,然后将查询到的数据值分配给当前数据的偏移量。此外,表中相应类别的值增加1。在获取所有数据的类内偏移后,使用数据的类别索引和类内偏移将同一类别内的时间序列进行哈希。
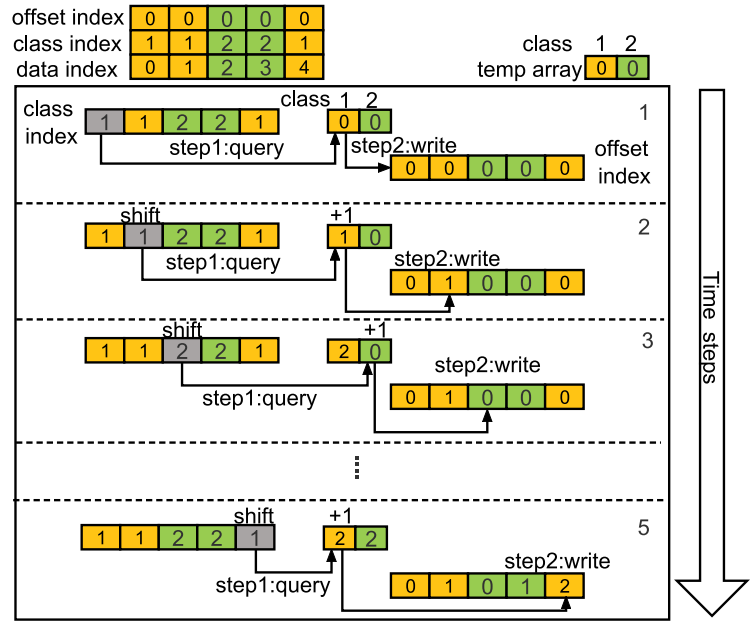
图2:类内偏移计算
基于上图中所示的串行方法,本文在GPU上设计了一种并行方法。如下图所示,数据被分成几个桶(bucket)。每个桶都有固定的大小,并且每个桶分配给一个线程。假设有10个时间序列数据,类别数为3。
首先,根据数据索引和其类别索引计算数据的类内偏移。在获取类内偏移的过程中,本文将桶的数量设置为三个,每个桶分配给一个独立的线程。每个线程使用图2中所示的串行方法独立地获取类内偏移,从而得到每个数据的相对偏移(图3(a))。接下来,在每个线程中重新排序局部临时数组(图3(b)),并聚合同一类别的局部临时数组,以获得通过exclusive scan更新的全局临时数组。更新后的全局临时数组中的元素表示不同桶中同一类别数据(具有相同颜色)的起始索引。然后,将全局临时数组重新映射回每个线程的局部临时数组,以获取所需的全局偏移。
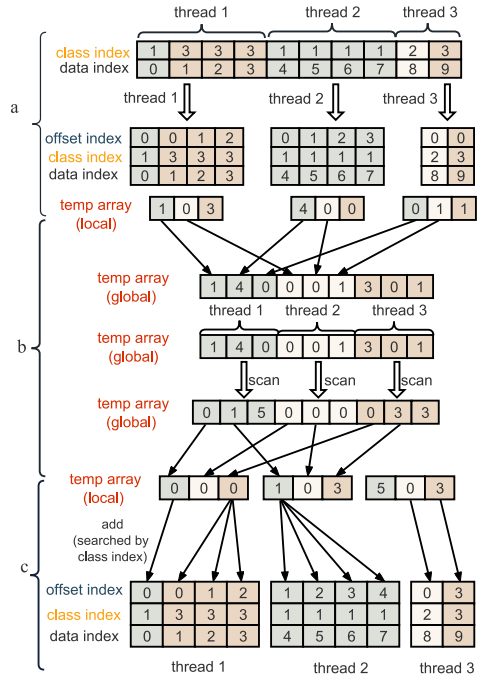
图3:并行类内偏移计算
假设每个时间序列数据的长度为4。基于全局偏移数组,可以进行并行数据哈希排序,如图4所示。为了实现并行排序,本文将所有线程沿两个维度分布,其中x方向的维度对应于每一行,y方向的维度对应于每一列。数据中的每个数字可以由x方向和y方向的线程ID确定。每个数据的位置将通过查询偏移索引和类别索引来确定。例如,要哈希第三个时间序列数据的第一个数,需查询与第三个数据对应的偏移索引和类别索引。其类别索引为3,偏移索引为1。随后通过查询类别索引找到第三类的起始地址,每个类的起始地址是通过对所有类进行exclusive scan得到的。接下来,使用偏移索引确定要映射的数据的类内偏移地址。此时,查询数据的类内偏移为1。将偏移乘以数据大小,然后加上查询到的类别起始地址(24)和线程y维度ID,以获取数据哈希后的位置。
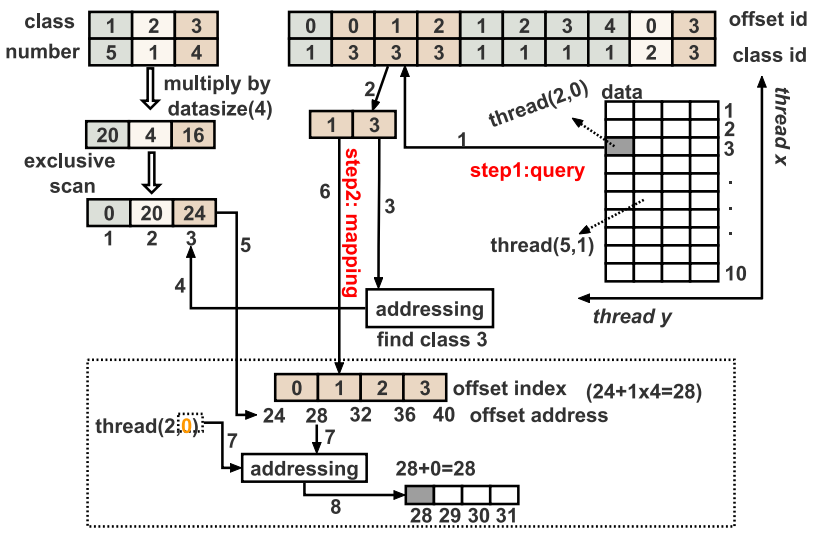
图4:并行数据hash
3.2、并行类中心计算
本文的设计结合了幂迭代和cuSOLVER。具体而言,幂迭代可以直接找到与最大绝对值特征值相对应的特征向量。由于每个类计算是独立的,可以使用CUDA流来优化。下列算法展示了求解类中心的过程。首先,迭代遍历每个数据类别,以确定第i类是否包含数据(第2-6行)。如果数据存在,将任务分配给处理该数据的第i个流(第7行)。接下来,获取矩阵M(第8-10行),并使用幂迭代方法找到与M的最大绝对特征值相对应的特征向量(第11-17行)。此外,本文选择时间序列的长度作为幂迭代的迭代次数。鉴于矩阵的最大特征值可能是重根,因此需要同时检查特征值的正确性和相应特征向量计算的正确性(第18-25行)。如果特征值小于等于零,或者特征向量计算不正确(第25行),使用cuSOLVER找到与最大特征值相对应的特征向量(第26行),并将其用作类的新质心。

3.3、并行类分配
在相似性计算过程中,可以使用快速傅里叶变换将互相关计算转化为element-wise复数乘法。尽管可以应用cuFFT进行并行的快速傅里叶变换和逆变换,但与element-wise操作相比,它们的开销微不足道。因此,本文的相似性计算设计侧重于在GPU上高效实现element-wise乘法。
为了减少内核启动的开销,本文将归一化操作和element-wise结合起来。本文在向量相乘之前并行地计算每个时间序列数据的L2范数和每个类中心的L2范数。具体来说,本文设置了两个kernel(图5a),第一个kernel设置m + k个线程,其中m是时间序列数据的数量,k是类中心的数量,以获取每个时间序列和类中心的平方和。在第二个kernel中,本文设置了m个线程(m >> k),将每个时间序列与所有类中心的L2范数相乘。图5(b)展示了求解所有时间序列数据相似性的并行过程。在这里,本文将线程块和线程设置为三维。X维度是时间序列的长度映射, y维度是时间序列数据数量的映射, z维度表示类中心数量的映射。norm(i, j)表示第i个时间序列数据和第j个类中心之间的L2范数。
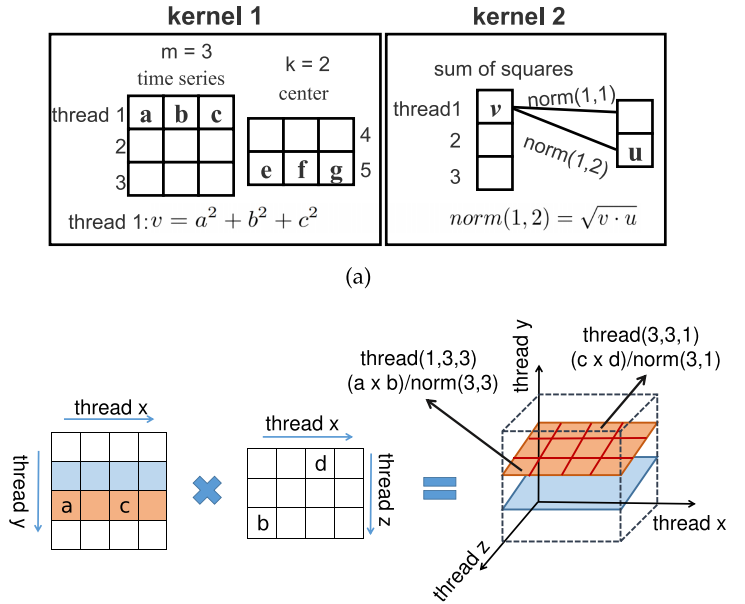
图5:并行相似度计算
四、实验结果
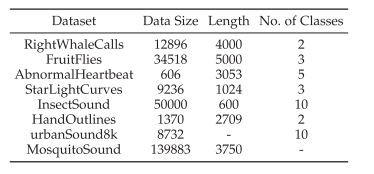
本文使用了由Ruiz等人开发的UCR &
UAE数据库,Dau等人开发的UCR数据库,以及常用于时间序列分类的urbansound8k数据集。这些数据集已经成为时间序列数据挖掘社区的重要资源。这些数据库中的数据集至少在数千篇发表的论文中被使用,它们从不同领域收集了时间序列数据,包括心电图、医学图像、光谱、传感器、音声等。本文从中选择了一些经典数据集进行性能评估和分析。详细信息如下表所示。
4.1、加速效果
本文对Paparrizos等人提供的算法1进行了CPU和GPU实现的比较,其中GPU版本使用了PyTorch进行实现。此外,本文还比较了在流行的时间序列分析框架tslearn中实现的k-Shape算法和dtw-kmeans算法。值得注意的是,tslearn中实现的k-Shape算法在初始迭代中选择随机初始化质心。对于CPU算法,本文选择了Intel(R) Xeon(R) Gold 6354 18核36线程作为硬件测试环境。由于k-Shape算法的原始论文在16线程环境中与其他算法进行了比较,因此本文选择了16线程作为CPU比较的基准。对于GPU算法,本文使用了NVIDIA A100作为硬件平台。
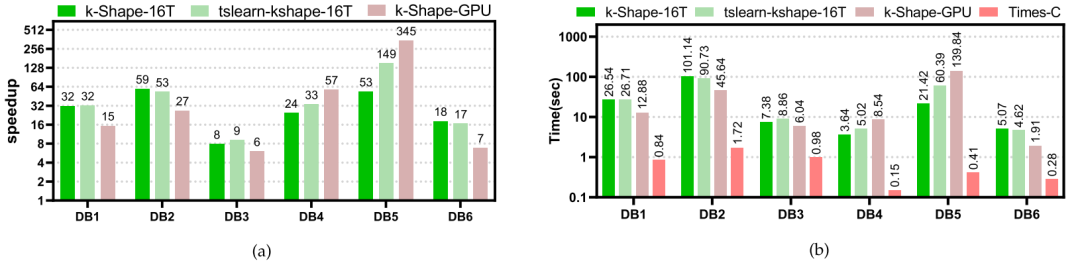
图6:与其他算法相比,Times-c算法获得的加速速度。
图6显示了Times-C与其他算法相比所实现的加速比。RightWhaleCalls(DB1)、InsectSound(DB5)和FruitFlies(DB2)是大型数据集。与其他数据集相比,Times-C算法在这些数据集上表现更好,表明Times-C算法在大型数据集上的性能更佳。数据集StarLightCurves(DB4)和InsectSound(DB5)的数据大小远大于其数据长度。与k-Shape-GPU算法相比,Times-C算法在这两个数据集上获得了更高的加速比。此外,AbnormalHeartbeat(DB3)数据集的长度远大于其大小。与k-Shape-GPU算法相比,Times-C算法获得的加速比不理想,表明相比于数据长度,在数据大小方面,Times-C可能在性能上获得更高的增益。
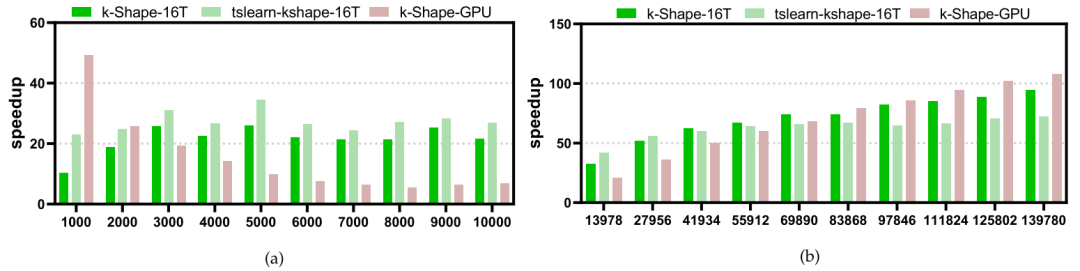
图7:Times-C算法对不同序列长度和序列大小的加速效果。
4.2、数据大小和数据长度的影响
在这一部分中,本文使用urbanSound8k和MosquitoSound数据集分别测试了数据长度和数据大小对算法执行时间的影响。
urbanSound8k是原始音频数据集,本文通过Python的librosa库对其进行了采样。从长度为1,000开始,采样步长为1,000,分别获得了序列长度为1,000到10,000的子数据集。图7(a)显示了Times-C算法与其他算法相比所实现的加速比。从图中可以看出,随着序列长度的增加,Times-C的加速比逐渐降低。然而,当序列长度达到7,000时,Times-C算法获得的加速比稳定下来,并不随着序列长度的增加而增加,这表明当序列长度增加到一定值后,Times-C算法的加速是较为稳定的。另一方面,在序列长度相对较短时,Times-C算法相对于k-Shape-GPU算法获得的性能提升较大,而减小序列长度将使序列大小更加突出。这表明在序列大小占主导地位时,k-Shape-GPU算法无法获得良好的性能优势。
MosquitoSound数据集是一个大小为139,883,长度为3,750的数据集。为了测试数据大小对算法执行时间的影响,本文对数据集进行了分段,并将原始数据集分成大小为1/10、2/10…10/10的子数据集。图7(b)显示了Times-C算法与其他算法相比所实现的加速比。从图中可以看出,随着序列大小的增加,Times-C的加速比逐渐增加。此外,在序列大小方面,Times-C比序列长度方面获得了更高的性能提升。与k-Shape-GPU算法相比,随着序列大小的增加,Times-C算法获得的加速速度增加得更为显著。
五、总结
时间序列数据分析不仅在日常生活中成为一种重要的数据处理方法,而且也广泛应用于大型科学设施中。本文分析了经典的时间序列聚类算法k-Shape,并将其分为三个主要任务:数据聚合、类中心提取和相似度计算。本文对这三个任务进行了并行优化,实现了显著的加速效果。此外,文章提出的并行方法并不局限于时间序列聚类。例如,类中心提取中的某些技术可以用来解决与最大特征值及其对应特征向量的相关问题。




 ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง
ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง





