Matlab 灰狼优化算法优化极限学习机(GWO-ELM)回归预测

✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，matlab项目合作可私信。

🍎个人主页：Matlab科研工作室

🍊个人信条：格物致知。

更多Matlab完整代码及仿真定制内容点击👇

智能优化算法       神经网络预测       雷达通信      无线传感器        电力系统

信号处理              图像处理               路径规划       元胞自动机        无人机

⛄ 内容介绍

在当今数据驱动的世界中，数据回归预测是一项重要的任务。它可以帮助我们预测未来的趋势和模式，为决策提供有力的支持。然而，由于数据的复杂性和噪声的存在，准确地进行回归预测并不容易。为了解决这个问题，研究人员提出了许多机器学习算法，并不断改进它们的性能。

极限学习机（ELM）是一种新兴的机器学习算法，它在回归预测任务中表现出色。ELM的核心思想是通过随机生成一组隐含层神经元的权重和偏置，将输入数据映射到隐含层。然后，通过线性回归方法将隐含层的输出与目标值进行拟合。ELM具有训练速度快、泛化能力强等优点，因此在实际应用中得到了广泛的应用。

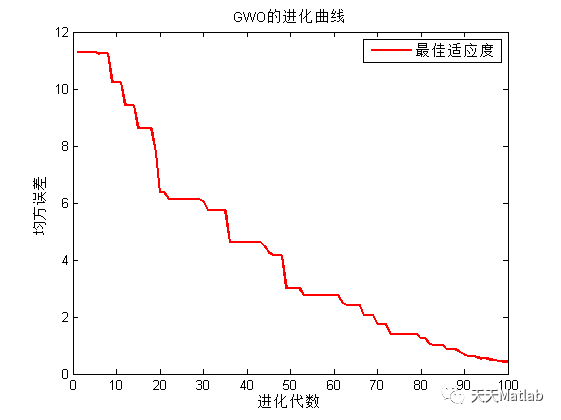
然而，ELM算法在处理一些复杂的问题时仍然存在一些挑战。为了进一步提高ELM的性能，研究人员将其与优化算法相结合，以寻找最佳的权重和偏置。灰狼算法（GWO）是一种基于群体智能的优化算法，模拟了灰狼群体的行为。它通过模拟灰狼的捕食行为来寻找最优解。将GWO与ELM相结合，可以有效地优化ELM的性能，提高回归预测的准确性。

GWO-ELM算法的实现过程如下。首先，通过随机生成一组灰狼的位置和速度来初始化灰狼种群。然后，根据每个灰狼的适应度值，选择最优的灰狼作为领导者。接下来，通过模拟灰狼的捕食行为，更新灰狼的位置和速度。最后，使用更新后的灰狼位置和速度来优化ELM的权重和偏置。重复这个过程，直到达到预定的停止条件。

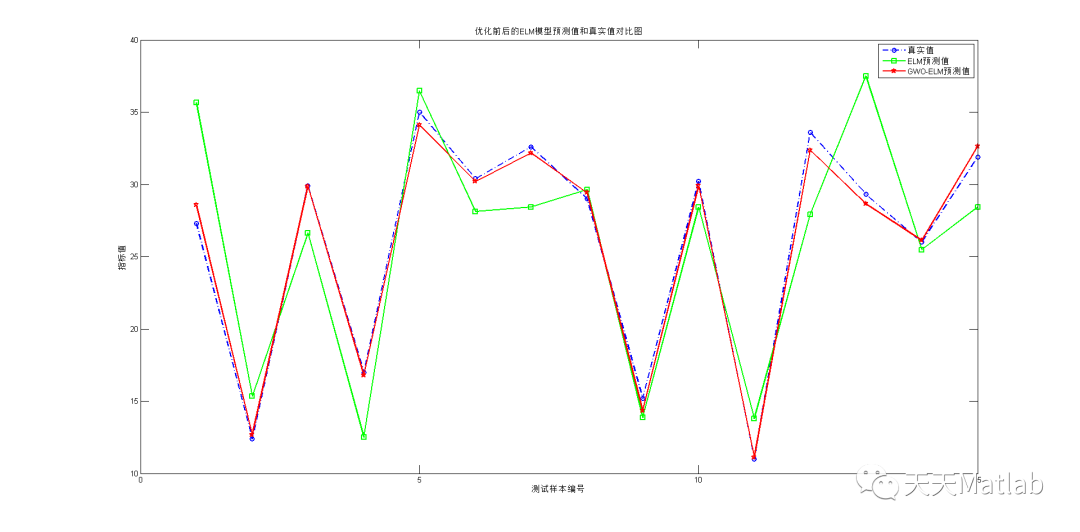
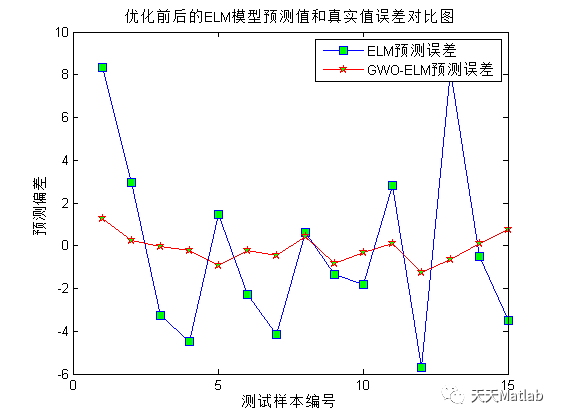
通过将GWO与ELM相结合，我们可以获得更好的回归预测结果。实验证明，GWO-ELM算法在多个数据集上的表现优于传统的ELM算法。它能够更好地适应复杂的数据模式，提高回归预测的准确性和稳定性。

总结起来，ELM回归预测是一项重要的任务，可以帮助我们预测未来的趋势和模式。为了提高ELM算法的性能，我们可以使用灰狼算法进行优化。GWO-ELM算法通过模拟灰狼的捕食行为，优化ELM的权重和偏置，从而提高回归预测的准确性。实验证明，GWO-ELM算法在多个数据集上表现优于传统的ELM算法。因此，GWO-ELM算法是一种值得尝试的方法，可以在实际应用中取得良好的效果。

希望通过本文的介绍，读者对于基于灰狼算法优化极限学习机GWO-ELM实现数据回归预测有了更深入的了解。在未来的研究和实践中，我们可以进一步探索和改进这个方法，以应对更加复杂的数据回归预测问题。

⛄ 部分代码

% BS2RV.m - Binary string to real vector%% This function decodes binary chromosomes into vectors of reals. The% chromosomes are seen as the concatenation of binary strings of given% length, and decoded into real numbers in a specified interval using% either standard binary or Gray decoding.%% Syntax: Phen = bs2rv(Chrom,FieldD)%% Input parameters:%% Chrom - Matrix containing the chromosomes of the current% population. Each line corresponds to one% individual's concatenated binary string% representation. Leftmost bits are MSb and% rightmost are LSb.%% FieldD - Matrix describing the length and how to decode% each substring in the chromosome. It has the% following structure:%% [len; (num)% lb; (num)% ub; (num)% code; (0=binary | 1=gray)% scale; (0=arithmetic | 1=logarithmic)% lbin; (0=excluded | 1=included)% ubin]; (0=excluded | 1=included)%% where% len - row vector containing the length of% each substring in Chrom. sum(len)% should equal the individual length.% lb,% ub - Lower and upper bounds for each% variable. % code - binary row vector indicating how each% substring is to be decoded.% scale - binary row vector indicating where to% use arithmetic and/or logarithmic% scaling.% lbin,% ubin - binary row vectors indicating whether% or not to include each bound in the% representation range%% Output parameter:%% Phen - Real matrix containing the population phenotypes.
%% Author: Carlos Fonseca, Updated: Andrew Chipperfield% Date: 08/06/93, Date: 26-Jan-94
function Phen = bs2rv(Chrom,FieldD)
% Identify the population size (Nind)% and the chromosome length (Lind)[Nind,Lind] = size(Chrom);
% Identify the number of decision variables (Nvar)[seven,Nvar] = size(FieldD);
if seven ~= 7 error('FieldD must have 7 rows.');end
% Get substring propertieslen = FieldD(1,:);lb = FieldD(2,:);ub = FieldD(3,:);code = ~(~FieldD(4,:));scale = ~(~FieldD(5,:));lin = ~(~FieldD(6,:));uin = ~(~FieldD(7,:));
% Check substring properties for consistencyif sum(len) ~= Lind, error('Data in FieldD must agree with chromosome length');end
if ~all(lb(scale).*ub(scale)>0) error('Log-scaled variables must not include 0 in their range');end
% Decode chromosomesPhen = zeros(Nind,Nvar);
lf = cumsum(len);li = cumsum([1 len]);Prec = .5 .^ len;
logsgn = sign(lb(scale));lb(scale) = log( abs(lb(scale)) );ub(scale) = log( abs(ub(scale)) );delta = ub - lb;
Prec = .5 .^ len;num = (~lin) .* Prec;den = (lin + uin - 1) .* Prec;
for i = 1:Nvar, idx = li(i):lf(i); if code(i) % Gray decoding Chrom(:,idx)=rem(cumsum(Chrom(:,idx)')',2); end Phen(:,i) = Chrom(:,idx) * [ (.5).^(1:len(i))' ]; Phen(:,i) = lb(i) + delta(i) * (Phen(:,i) + num(i)) ./ (1 - den(i));end
expand = ones(Nind,1);if any(scale) Phen(:,scale) = logsgn(expand,:) .* exp(Phen(:,scale));end

⛄ 运行结果

⛄ 参考文献

[1] 刘振男、杜尧、韩幸烨、和鹏飞、周正模、曾天山.基于遗传算法优化极限学习机模型的干旱预测——以云贵高原为例[J].人民长江, 2020, 51(8):6.DOI:CNKI:SUN:RIVE.0.2020-08-003.

[2] 郑小霞,蒋海生,刘静,等.基于变分模态分解与灰狼算法优化极限学习机的滚动轴承故障诊断[J].轴承, 2021(9):6.

[3] 王桥,魏孟,叶敏,等.基于灰狼算法优化极限学习机的锂离子电池SOC估计[J].储能科学与技术, 2021.DOI:10.19799/j.cnki.2095-4239.2020.0389.

❤️部分理论引用网络文献，若有侵权联系博主删除

❤️ 关注我领取海量matlab电子书和数学建模资料

🍅 私信完整代码和数据获取及论文数模仿真定制

1 各类智能优化算法改进及应用

生产调度、经济调度、装配线调度、充电优化、车间调度、发车优化、水库调度、三维装箱、物流选址、货位优化、公交排班优化、充电桩布局优化、车间布局优化、集装箱船配载优化、水泵组合优化、解医疗资源分配优化、设施布局优化、可视域基站和无人机选址优化

2 机器学习和深度学习方面

卷积神经网络（CNN）、LSTM、支持向量机（SVM）、最小二乘支持向量机（LSSVM）、极限学习机（ELM）、核极限学习机（KELM）、BP、RBF、宽度学习、DBN、RF、RBF、DELM、XGBOOST、TCN实现风电预测、光伏预测、电池寿命预测、辐射源识别、交通流预测、负荷预测、股价预测、PM2.5浓度预测、电池健康状态预测、水体光学参数反演、NLOS信号识别、地铁停车精准预测、变压器故障诊断

2.图像处理方面

图像识别、图像分割、图像检测、图像隐藏、图像配准、图像拼接、图像融合、图像增强、图像压缩感知

3 路径规划方面

旅行商问题（TSP）、车辆路径问题（VRP、MVRP、CVRP、VRPTW等）、无人机三维路径规划、无人机协同、无人机编队、机器人路径规划、栅格地图路径规划、多式联运运输问题、车辆协同无人机路径规划、天线线性阵列分布优化、车间布局优化

4 无人机应用方面

无人机路径规划、无人机控制、无人机编队、无人机协同、无人机任务分配、无人机安全通信轨迹在线优化

5 无线传感器定位及布局方面

传感器部署优化、通信协议优化、路由优化、目标定位优化、Dv-Hop定位优化、Leach协议优化、WSN覆盖优化、组播优化、RSSI定位优化

6 信号处理方面

信号识别、信号加密、信号去噪、信号增强、雷达信号处理、信号水印嵌入提取、肌电信号、脑电信号、信号配时优化

7 电力系统方面

微电网优化、无功优化、配电网重构、储能配置

8 元胞自动机方面

交通流 人群疏散 病毒扩散 晶体生长

9 雷达方面

卡尔曼滤波跟踪、航迹关联、航迹融合