大模型的能力边界在哪里？来自范畴论视角的答案

导语

如果用一个范畴论公式来描绘大模型的能力，它应该是什么样？本文作者、清华大学交叉信息学院助理教授袁洋给出了这样一个公式。他认为，现代科学基于数学，现代数学基于范畴论，如果范畴论可以照耀现代数学的各个分支，它也一定可以照亮通用人工智能的前进之路。
为了探索数学与人工智能深度融合的可能性，集智俱乐部联合同济大学特聘研究员陈小杨、清华大学交叉信息学院助理教授袁洋、南洋理工大学副教授夏克林三位老师，共同发起“人工智能与数学”读书会，希望从 AI　for　Math，Math　for　AI 两个方面深入探讨人工智能与数学的密切联系。本读书会是“AI+Science”主题读书会的第三季。读书会自9月15日开始，每周五晚20:00-22:00，预计持续时间8～10周。欢迎感兴趣的朋友报名参与！
研究领域：范畴论，人工智能，机器学习，大语言模型，AI + Math袁洋 | 作者

目录

1. 范畴论是什么？

2. 监督学习的范畴论视角

3. 自监督学习的范畴论视角

4. 提示调优（Prompt tuning）: 见多才能识广

5. 微调（Fine tuning）: 表征不丢信息

6. 讨论与总结

假如我们有无限的资源，比如有无穷多的数据，无穷大的算力，无穷大的模型，完美的优化算法与泛化表现，请问由此得到的预训练模型是否可以用来解决一切问题？
这是一个大家都非常关心的问题，但已有的机器学习理论却无法回答。它与表达能力理论无关，因为模型无穷大，表达能力自然也无穷大。它与优化、泛化理论也无关，因为我们假设算法的优化、泛化表现完美。换句话说，之前理论研究的问题在这里不存在了！
今天，我给大家介绍一下我在ICML’2023发表的论文On the Power of Foundation Models，从范畴论的角度给出一个答案。
论文题目：On the Power of Foundation Models论文链接：https://proceedings.mlr.press/v202/yuan23b.html

范畴论是什么？

倘若不是数学专业的同学，对范畴论可能比较陌生。范畴论被称为是数学的数学，为现代数学提供了一套基础语言。现代几乎所有的数学领域都是用范畴论的语言描述的，例如代数拓扑、代数几何、代数图论等等。范畴论是一门研究结构与关系的学问，它可以看作是集合论的一种自然延伸：在集合论中，一个集合包含了若干个不同的元素；在范畴论中，我们不仅记录了元素，还记录了元素与元素之间的关系。
Martin Kuppe曾经画了一幅数学地图，把范畴论放到了地图的顶端，照耀着数学各个领域：
关于范畴论的介绍网上有很多，我们这里简单讲几个基本概念： • 范畴：一个范畴 C 包含很多对象，以及对象与对象之间的关系，例如 HomC(X,Y) 表示两个对象 X,Y 之间的关系。 • 函子：两个范畴 C 与 C′ 之间的函数被称为函子 F:C→C′ . 它不仅把 C 中的对象映射到 C′ ，同时还保持关系结构不变。

 • 自然映射：函子之间也可以有关系，被称为自然映射。

监督学习的范畴论视角

我给本科生教了4年机器学习，深刻感受到监督学习框架是其根本。这个框架极为优美：我们假设存在一个真实分布 D=(DX,DY) ，表示输入 X 和标签 Y 的分布。训练数据集 (Xtrain, Ytrain) 和测试数据集 (Xtest, Ytest) 都是从 D 中均匀采样得到的。我们希望能够学习一个函数 f:X→Y ，使得 f(x) 能够准确地计算出 x 的标签。为了达到这个目标，我们需要定义一个损失函数 L(f,x,y) ，用来度量 f(x) 和正确标签 y 的距离，这个距离自然是越接近于0越好。

过去十多年，人们围绕着监督学习框架进行了大量的研究，得到了很多优美的结论。但是，这一框架也限制了人们对AI算法的认识，让理解预训练大模型变得极为困难。例如，已有的泛化理论很难用来解释模型的跨模态学习能力。

用范畴论来理解监督学习，则会得到不一样的结果。我们可以把输入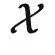空间与输出空间 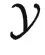 当做两个不同的范畴，把具体的数据点 x 和 y 当做范畴中的对象。在范畴论中我们经常用大写字母表示对象，用花体字符表示范畴，所以下面我们切换符号，使用 X 和 Y 表示数据点。同时，我们也不再关心概率分布，而使用从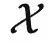到 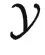  的一个函子表示输入与输出的正确关系。

在新的视角下，测试数据、训练数据就变成了从函子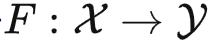中采样得到的输入输出数据。所以说，监督学习在讨论如下问题：

我们能不能通过采样函子的输入输出数据，学到这个函子？

注意到，在这个过程中我们没有考虑两个范畴 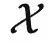,  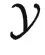内部的结构。实际上，监督学习没有对范畴内部的结构有任何假设，所以可以认为在两个范畴内部，任何两个对象之间都没有关系。因此，我们完全可以把 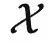和 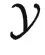 看作是两个集合。这个时候，泛化理论著名的 no free lunch 定理告诉我们，假如没有额外假设，那么学好从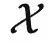到 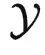  的函子这件事情是不可能的（除非有海量样本）。

为了处理这个问题，之前的泛化理论假设函子满足某些性质，相当于加了一个比较强的约束，就可以绕开 no free lunch 定理。但是，从范畴论的角度看，给函子加约束是一件很奇怪的事情：函子并不是一个实体，它只是描述了两个范畴之间的一些映射关系，是伴随着带有内部结构的范畴的出现而存在的——我们怎么可以说有些映射关系不能出现，有些可以出现呢？所以，正确的做法应该是对范畴结构加约束。举个例子，如果我们知道 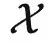 有线性结构，并且函子  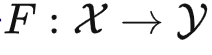保持了这个结构，那么我们一样可以绕开 no free lunch 定理，通过很少的样本学习 F。

乍看之下，这个新视角毫无用处。给范畴加约束也好，给函子加约束也好，似乎没什么本质区别。实际上，新视角更像是传统框架的阉割版本：它甚至没有提及监督学习中极为重要的损失函数的概念，也就无法用于分析训练算法的收敛或泛化性质。那么我们应该如何理解这个新视角呢？

我想，范畴论提供了一种鸟瞰视角。它本身不会也不应该替代原有的更具体的监督学习框架，或者用来产生更好的监督学习算法。相反，监督学习框架是它的“子模块”，是解决具体问题时可以采用的工具。因此，范畴论不会在乎损失函数或者优化过程——这些更像是算法的实现细节。它更关注范畴与函子的结构，并且尝试理解某个函子是否可学习。这些问题在传统监督学习框架中极为困难，但是在范畴视角下变得简单。

自监督学习的范畴论视角

预训练任务与范畴

在自监督学习框架中，数据集不再有标签。不过，我们还是可以对数据集设置预训练任务，学习数据集本身的信息。已有的预训练任务多种多样，比如对比学习，遮挡学习，语言模型等等。我们在预训练模型中学习的目标是 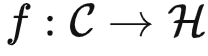 ，即把每个数据点 X 映射到它的特征表示 f(X)，使得这些特征表示可以用于解决预训练任务。

下面我们先明确在预训练任务下范畴的定义。实际上，倘若我们没有设计任何预训练任务，那么范畴中的对象之间就没有关系；但是设计了预训练任务之后，我们就将人类的先验知识以任务的方式，给范畴注入了结构。而这些结构就成为了大模型拥有的知识。

具体来说：

• 对比学习。正如我在《对比学习在学啥？》（https://zhuanlan.zhihu.com/p/634466306） 文章里介绍的，对比学习构建了一个相似图，使得任何两个对象之间的关系可以用一个相似度来表示，而这个相似度恰好对应于正样本的采样概率，即 被采样为一对正样本HomC(X,Y)∝Pr((X,Y)被采样为一对正样本) 。
• 遮挡学习。遮挡学习的意思是把一个对象的一部分内容遮挡起来，然后让模型预测遮挡的部分是什么。对于这个任务，我们可以把遮挡之后的对象当做 X ，把遮挡位置当做 Y ，然后将 HomC(X,Y) 定义为完整的对象本身。这样，每一组关系都对应一个遮挡学习问题的解决方案。

• 语言模型。对象 X 是一个句子，对象 Y 则是它的续写，只有最后一个词不同。例如， 我今天很开X=‘‘我今天很开”， 我今天很开心Y=‘‘我今天很开心”。语言模型关心的是 Pr(Y|X) ，我们把它定义为HomC(X,Y) 。

换句话说，当我们在一个数据集上定义了预训练任务之后，我们就定义了一个包含对应关系结构的范畴。预训练任务的学习目标，就是让模型把这个范畴学好。具体来说，我们看一下理想模型的概念。

理想模型

给定一个预训练模型 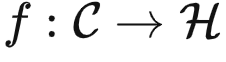，它什么时候是比较理想的呢？很简单，当它计算出的特征可以用来很方便地刻画范畴  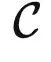内部关系的时候。对于这个概念不太明白的朋友，可以参见上一篇《对比学习在学啥？》（https://zhuanlan.zhihu.com/p/634466306），里面有一些直观的例子。

严格来说，给定由预训练任务定义的范畴 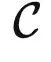 ，如果存在一个预定义的函数 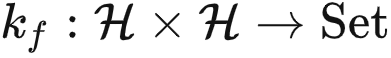，使得对任意的 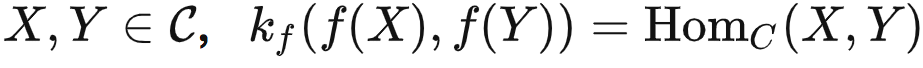，那么模型 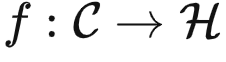就是理想的。

在这里，“数据无关”意味着 kf 是在看到数据之前就预先定义的；但下标 f 则表示kf可以通过黑盒调用的方式使用 f 和 f-1 这两个函数。换句话说， kf 是一个“简单”的函数，但可以借助模型 f 的能力来表示更复杂的关系。这一点可能不太好理解，我们用压缩算法来打个比方。压缩算法本身可能是数据相关的，比如它可能是针对数据分布进行了特殊优化。然而，作为一个数据无关的函数 kf ，它无法访问数据分布，但可以调用压缩算法来解压数据，因为“调用压缩算法”这一操作是数据无关的。

针对不同的预训练任务，我们可以定义不同的 kf ：

• 对比学习。在对比学习中，任何两个对象之间的关系可以使用一个实数表示，因此 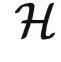 可以被看作以 kf 为核函数的空间。例如，在SimCLR[1]和MoCo[2]中， kf 是一个简单的高斯核函数。
• 遮挡学习。就像之前说的，我们用 X 表示可见部分， Y 表示遮蔽部分。在MAE[3]中，我们用f(X) 和 f(Y) 计算这两个部分的表征。然后， kf 将 f(X) 和 f(Y) 进行拼接，并使用 f-1(⋅) 恢复完整的对象。

• 语言模型。我们想要计算 Pr(Y|X) ，其中 Y 是 X 的续写，只有最后一个词不同。kf 运行一个线性函数（可以预先定义好，不参与优化）和一个Softmax函数来计算下一个词的概率分布。基于这个分布，kf 运行f-1(f(Y)) 来提取 Y，并计算 Pr(Y|X) 。

因此，我们可以这么说：预训练学习的过程，就是在寻找理想模型 f 的过程。

可是，即使 kf 是确定的，根据定义，理想模型也并不唯一。理论上说，模型 f 可能具有超级智能，即使在不学习 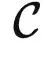 中数据的前提下也能做任何事情。在这种情况下，我们无法对 f 的能力给出有意义的论断。因此，我们应该看看问题的另一面：

给定由预训练任务定义的范畴 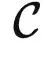 ，对于任何一个理想的 f ，它能解决哪些任务？

这是我们在本文一开始就想回答的核心问题。我们先介绍一个重要概念。

米田嵌入

我们定义米田嵌入函子为 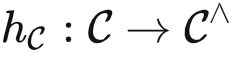。针对任何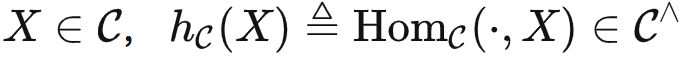，即可以接受输入 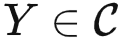并输出 HomC(Y,X)。

简单来说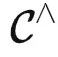，  是一个专门存放各种函子的范畴（被称为预层范畴），输入一个对象 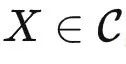，输出一个集合。而  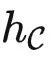接受 X 并输出关于 X 的所有关系。如果  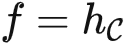，我们可以把 kf(f(X),f(Y)) 定义成先使用 f-1(f(X)) 计算出 X ，再将 X 传给 f(Y)=HomC(⋅,Y) ，得到 HomC(X,Y) 。所以我们知道  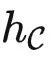是理想的。

很容易证明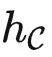，  是能力最弱的理想模型，因为给定其他理想模型 f 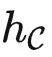，  中的所有关系也包含在 f 中。同时，它也是没有其他额外假设前提之下，预训练模型学习的最终目标。因此，为了回答我们的核心问题，我们下面专门考虑 。

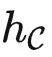提示调优（Prompt tuning）: 见多才能识广

为了理解模型能够解决哪些任务，我们需要先明确什么是任务。一个任务 T 可以看作是 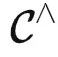 中的函子。我们说模型解决了一个任务 T∈ 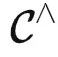，如果对于任何输入  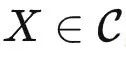  ，模型输出的答案与 T(X) 是同构的。在范畴论中，当两个对象（或函子）是同构的，我们就将它们视为相等的。我们不去考虑如何让两个同构的对象变得完全一致，因为这在现代神经网络中并不是问题。例如，如果两个对象 X 和 Y 之间存在一个同构映射，使得 ϕ(X)=Y，那么神经网络可以轻松地找到这个 ϕ 。

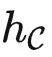  能否解决某个任务 T ？要回答这个问题，我们先介绍范畴论中最重要的一个定理。

米田引理

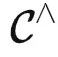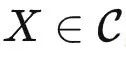米田引理：对于 T∈ 和   ，有  。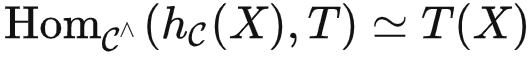

给定任务 T∈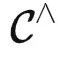，提示调优意味着我们需要冻结模型的参数，并仅使用任务特定提示 P （通常为文本或图像），加上输入 X ，得到输出 T(X) 。因此，提示 P 和输入 X 是模型的输入。由米田引理，如果我们直接将 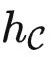(X) 和 T 作为  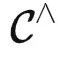中的函子发送到 kf，由于 kf 是  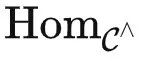函数的实现，我们有

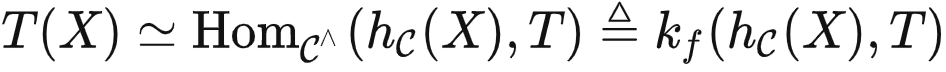
即，kf 可以用这两种表征计算出 T(X) 。然而，注意到任务提示 P 必须通过 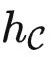 而非 kf 发送，这意味着我们会得到 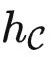(P) 而非 T 作为 kf 的输入。这引出了范畴论中另一个重要的定义。

可表函子：对于 T∈ 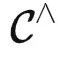 ，如果存在某个 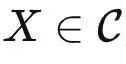使得 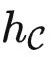(X)≃T ，则称 T 是可表的。X 被称为 T 的代表。

基于这个定义，我们可以得到如下定理（证明略去）。

定理1与推论

定理1. 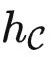  可以通过提示调优解决任务 T ，当且仅当任务 T∈  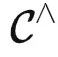 是可表的。当 T 可表时，最优的提示是 T 的代表。

换句话说，当我们设计一个提示词 P∈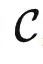 ，发现它有比较好的效果的时候，其实是因为它是（或者很接近）要解决的任务的一个代表。具体来说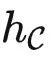，(P)≃T 。

值得一提的是，有些提示调优算法的提示不一定是范畴 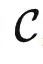  中的对象，可能是特征空间中的表征。这种方法有可能支持比可表任务更复杂的任务，但增强效果取决于特征空间的表达能力。下面我们提供定理1的一个简单推论。

推论1. 对于预测图像旋转角度的预训练任务[4]，提示调优不能解决分割或分类等复杂的下游任务。

证明：预测图像旋转角度的预训练任务会将给定图像旋转四个不同的角度：0°, 90°, 180°, 和 270°，并让模型进行预测。因此，这个预训练任务定义的范畴将每个对象都放入一个包含4个元素的群中。显然，像分割或分类这样的任务不能由这样简单的对象表出。

推论1有点反直觉，因为原论文提到[4]，使用该方法得到的模型可以部分解决分类或分割等下游任务。然而，在我们的定义中，解决任务意味着模型应该为每个输入生成正确的输出，因此部分正确并不被视为成功。这也与我们文章开头提到的问题相符：在无限资源的支持下，预测图像旋转角度的预训练任务能否用于解决复杂的下游任务？推论1给出了否定的答案。

微调（Fine tuning）: 表征不丢信息

提示调优的能力有限，那么微调算法呢？基于米田函子扩展定理（参见[5]中的命题2.7.1），我们可以得到如下定理。

定理2. 给定足够的资源，针对任何任务F: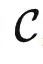→Set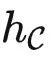，的表征可以用于学习 G: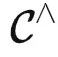→Set ，使得 。

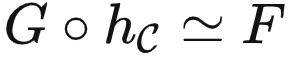定理2考虑的下游任务是基于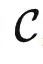 的结构，而不是数据集中的数据内容。因此，之前提到的预测旋转图片角度的预训练任务定义的范畴仍然具有非常简单的群结构。但是根据定理2，我们可以用它解决更多样化的任务。例如，我们可以将所有对象映射到同一个输出，这是无法通过提示调优来实现的。定理2明确了预训练任务的重要性，因为更好的预训练任务将创建更强大的范畴 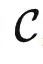，从而进一步提高了模型的微调潜力。

对于定理2有两个常见的误解。首先，即使范畴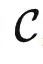 包含了大量信息，定理2只提供了一个粗糙的上界，说 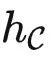记录了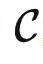 中所有的信息，有潜力解决任何任务，而并没有说任何微调算法都可以达到这个目的。其次，定理2乍看像是过参数化理论。然而，它们分析的是自监督学习的不同步骤。过参数化分析的是预训练步骤，说的是在某些假设下，只要模型足够大且学习率足够小，对于预训练任务，优化和泛化误差将非常小。而定理2分析的则是预训练后的微调步骤，说该步骤有很大潜力。

讨论与总结

监督学习与自监督学习。从机器学习的角度来看，自监督学习仍然是一种监督学习，只是获取标签的方式更巧妙一些而已。但是从范畴论的角度来看，自监督学习定义了范畴内部的结构，而监督学习定义了范畴之间的关系。因此，它们处于人工智能地图的不同板块，在做完全不一样的事情。

与ChatGPT的关系。很多朋友可能会关心本文的结论应该如何应用到ChatGPT等聊天模型上去？简单来说，ChatGPT等模型不光有预训练的过程，还有RLHF等进一步微调部分，所以定理1的结论没法直接应用。不过，它也可以看作是对 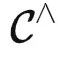 进行微调的一种变体，获得了强大的能力。这也符合数学家们使用  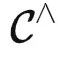的感受：很多问题在原来的范畴 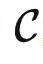中很困难，但是往往在 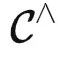中就迎刃而解。

适用场景。由于本文开头考虑了无限资源的假设，导致很多朋友可能会认为，这些理论只有在虚空之中才会真正成立。其实并非如此。在我们真正的推导过程中，我们只是考虑了理想模型与 kf 这一预定义的函数。实际上，只要 kf 确定了之后，任何一个预训练模型 f （哪怕是在随机初始化阶段）都可以针对输入 X∈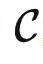 计算出 f(X) ，从而使用 kf 计算出两个对象的关系。换句话说，只要当 kf 确定之后，每个预训练模型都对应于一个范畴，而预训练的目标不过是将这个范畴不断与由预训练任务定义的范畴对齐而已。因此，我们的理论针对每一个预训练模型都成立。

核心公式。很多人说，如果AI真有一套理论支撑，那么它背后应该有一个或者几个简洁优美的公式。我想，如果需要用一个范畴论的公式来描绘大模型能力的话，它应该就是我们之前提到的：

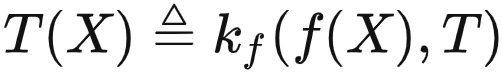
对于大模型比较熟悉的朋友，在深入理解这个公式的含义之后，可能会觉得这个式子在说废话，不过是把现在大模型的工作模式用比较复杂的数学式子写出来了而已。

但事实并非如此。现代科学基于数学，现代数学基于范畴论，而范畴论中最重要的定理就是米田引理。我写的这个式子将米田引理的同构式拆开变成了不对称的版本，却正好和大模型的打开方式完全一致。

我认为这一定不是巧合。如果范畴论可以照耀现代数学的各个分支，它也一定可以照亮通用人工智能的前进之路。

本文灵感源于与北京智源人工智能研究院千方团队的长期紧密合作。

参考文献

[1] https://arxiv.org/abs/2002.05709

[2] https://arxiv.org/abs/1911.05722

[3] https://arxiv.org/abs/2111.06377

[4] abhttps://arxiv.org/abs/1803.07728

[5] Masaki Kashiwara, P. S. Categories and Sheaves. Springer, 2006. https://link.springer.com/book/10.1007/3-540-27950-4

本文首发于作者知乎：https://zhuanlan.zhihu.com/p/634467074

作者简介

袁洋，清华大学交叉信息学院助理教授。2012年毕业于北京大学计算机系，2018年获得美国康奈尔大学计算机博士学位，师从Robert Kleinberg教授。在博士期间，于2014年-2015年前往微软新英格兰研究院做访问学生，并于2016年秋季前往美国普林斯顿大学做访问学生。2018-2019年前往麻省理工学院大数据科学学院（MIFODS）做博士后。袁洋的主要研究方向是智能医疗、AI基础理论、应用范畴论。

人工智能与数学读书会启动

数十年来，人工智能的理论发展和技术实践一直与科学探索相伴而生，尤其在以大模型为代表的人工智能技术应用集中爆发的当下，人工智能正在加速物理、化学、生物等基础科学的革新，而这些学科也在反过来启发人工智能技术创新。在此过程中，数学作为兼具理论属性与工具属性的重要基础学科，与人工智能关系甚密，相辅相成。一方面，人工智能在解决数学领域的诸多工程问题、理论问题乃至圣杯难题上屡创记录。另一方面，数学持续为人工智能构筑理论基石并拓展其未来空间。这两个关键领域的交叉融合，正在揭开下个时代的科学之幕。

为了探索数学与人工智能深度融合的可能性，集智俱乐部联合同济大学特聘研究员陈小杨、清华大学交叉信息学院助理教授袁洋、南洋理工大学副教授夏克林三位老师，共同发起“人工智能与数学”读书会，希望从 AI　for　Math，Math　for　AI 两个方面深入探讨人工智能与数学的密切联系。本读书会是“AI+Science”主题读书会的第三季。读书会自9月15日开始，每周五晚20:00-22:00，预计持续时间8～10周。欢迎感兴趣的朋友报名参与！

详情请见：

人工智能与数学读书会启动：AI for Math，Math for AI

推荐阅读

1.  探索“AI 大统一理论”：科学启发的机器学习理论2. 几何深度学习：让物理世界拥有AI | 黄文炳分享整理3.  AI 还需要理论么？4. 张江：第三代人工智能技术基础——从可微分编程到因果推理 | 集智学园全新课程5. 成为集智VIP，解锁全站课程／读书会6. 加入集智，一起复杂！

点击“阅读原文”，加入读书会