✅作者简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,matlab项目合作可私信。
🍎个人主页:Matlab科研工作室
🍊个人信条:格物致知。
更多Matlab完整代码及仿真定制内容点击👇
🔥 内容介绍
在结构工程领域,了解和分析结构的模态参数对于评估结构的健康状况和性能至关重要。传统上,模态参数的识别通常需要进行大量的实验测量和复杂的数据处理。然而,随着技术的不断发展,一种新的算法——SSI-COV算法,为自动识别线状结构的模态参数提供了一种更高效和准确的方法。
SSI-COV算法是基于结构系统辨识(SSI)理论的一种方法,它利用环境振动数据来识别结构的模态参数。该算法通过将结构的动力响应与环境激励信号进行相关分析,从而提取出结构的模态参数,如固有频率、阻尼比和模态形态等。
与传统的模态识别方法相比,SSI-COV算法具有以下几个优势。首先,它不需要进行额外的激励实验,只需要利用结构在自然环境中的振动响应数据即可。这样可以大大减少实验的时间和成本。其次,该算法能够自动识别多个模态参数,而无需人工干预。这对于复杂的结构系统来说尤为重要,因为它们可能具有多个模态。
在使用SSI-COV算法进行模态参数识别时,需要注意一些关键的步骤。首先,需要对环境振动数据进行预处理,包括滤波和去噪等。然后,需要选择合适的相关函数来计算结构的动力响应与激励信号之间的相关性。最后,通过对相关函数进行特征提取和模型拟合,可以得到结构的模态参数。
虽然SSI-COV算法在模态参数识别方面具有许多优势,但也存在一些局限性。首先,该算法对环境振动数据的质量要求较高,需要保证数据的准确性和完整性。其次,该算法对结构的线性特性有一定的假设,因此在应用于非线性结构时可能会出现一些误差。
综上所述,SSI-COV算法是一种有效的方法,可用于自动识别线状结构的模态参数。它可以减少实验的时间和成本,并提供准确和全面的模态参数信息。然而,在实际应用中,我们仍然需要根据具体情况选择合适的算法和方法,以确保模态参数的准确性和可靠性。
📣 部分代码
function [h] = plotStabDiag(fn,Az,fs,stablity_status,Nmin,Nmax)% -------------------------------------------------------------------------% [h] = plotStabDiag(fn,Az,fs,stablity_status,Nmin,Nmax) plots the% stabilization diagram of the identified eigen frequencies as a function% of the model order, calculated with the SSI-COV method.% -------------------------------------------------------------------------% Input:% fn: cell : eigen frequencies identified for multiple system orders.% Az : vector: Time serie of acceleration response (illustrative purpose)% fs: sampling frequency% stablity_status: cell of stability status for each model order% Nmin: scalar: minimal number of model order% Nmax: scalar: maximal number of model order% Output: h: handle of the figure% -------------------------------------------------------------------------% See also: SSICOV.m% -------------------------------------------------------------------------% Author: Etienne Cheynet, UIS% Updated on: 08/03/2016% -------------------------------------------------------------------------Npoles =Nmin:1:Nmax;[Saz,f]=pwelch(Az,[],[],[],fs);h = figure;ax1 = axes;hold on;box onfor jj=0:4, y = []; x = []; for ii=1:numel(fn) ind = find(stablity_status{ii}==jj); x = [x;fn{ii}(ind)']; y = [y;ones(numel(ind),1).*Npoles(ii)]; end x1{jj+1}=x; y1{jj+1}=y;endh1=plot(x1{1},y1{1},'k+','markersize',5);% new poleh2=plot(x1{2},y1{2},'ko','markerfacecolor','r','markersize',5); % stable poleh3=plot(x1{3},y1{3},'bo','markersize',5); % pole with stable frequency and vectorh4=plot(x1{4},y1{4},'gsq','markersize',5); % pole with stable frequency and dampingh5=plot(x1{5},y1{5},'gx','markersize',5); % pole with stable frequencyif isempty(h1), h1=0;elseif isempty(h2), h2=0;elseif isempty(h3), h3=0;elseif isempty(h4), h4=0;elseif isempty(h5), h5=0;endH = [h1(1),h2(1),h3(1),h4(1),h5(1)];legend(H,... 'new pole',... 'stable pole',... 'stable freq. & MAC',... 'stable freq. & damp.',... 'stable freq.',... 'location','Northoutside','orientation','horizontal');ylabel('number of poles');xlabel('f (Hz)')xlim([0,max([fn{:}])*1.1])hold offax2 = axes('YAxisLocation', 'Right');linkaxes([ax1,ax2])plot(ax2,f,Saz./max(Saz).*0.001,'k');ax2.YLim = [0,Nmax];ax2.XLim = [0,max([fn{:}])*1.1];set(ax2,'yscale','log')ax2.Visible = 'off';ax2.XTick = [];ax2.YTick = [];set(gcf,'color','w')end
⛳️ 运行结果
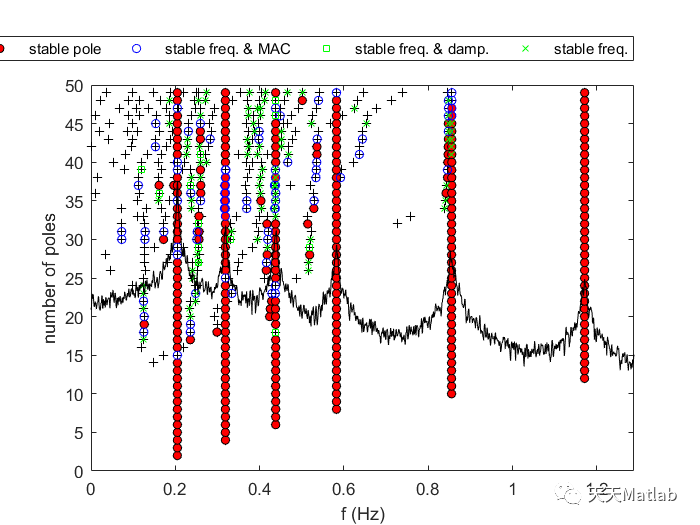
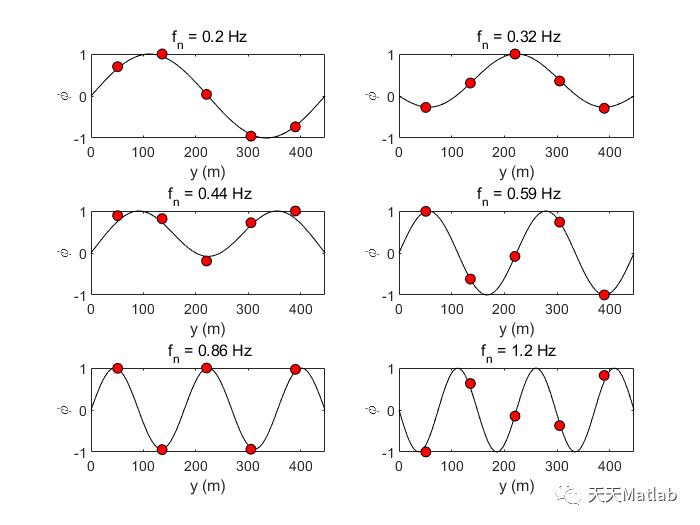
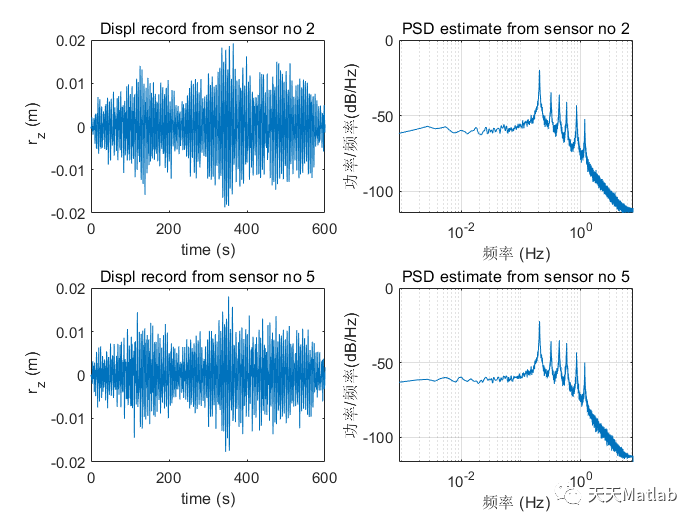
🔗 参考文献
[1] Magalhaes, F., Cunha, A., & Caetano, E. (2009). Online automatic identification of the modal parameters of a long span arch bridge. Mechanical Systems and Signal Processing, 23(2), 316-329.
[2] Cheynet, E., Jakobsen, J. B., & Snæbjörnsson, J. (2016).Buffeting response of a suspension bridge in complex terrain. Engineering Structures, 128, 474-487.
[3] Cheynet, E., Jakobsen, J. B., & Snæbjörnsson, J. (2017).Damping estimation of large wind-sensitive structures.Procedia Engineering, 199, 2047-2053.
[4] Cheynet, E., Snæbjörnsson, J., & Jakobsen, J. B. (2017).Temperature Effects on the Modal Properties of a Suspension Bridge.In Dynamics of Civil Structures, Volume 2 (pp. 87-93). Springer.
🎈 部分理论引用网络文献,若有侵权联系博主删除
🎁 关注我领取海量matlab电子书和数学建模资料
👇 私信完整代码和数据获取及论文数模仿真定制
1 各类智能优化算法改进及应用
生产调度、经济调度、装配线调度、充电优化、车间调度、发车优化、水库调度、三维装箱、物流选址、货位优化、公交排班优化、充电桩布局优化、车间布局优化、集装箱船配载优化、水泵组合优化、解医疗资源分配优化、设施布局优化、可视域基站和无人机选址优化
2 机器学习和深度学习方面
卷积神经网络(CNN)、LSTM、支持向量机(SVM)、最小二乘支持向量机(LSSVM)、极限学习机(ELM)、核极限学习机(KELM)、BP、RBF、宽度学习、DBN、RF、RBF、DELM、XGBOOST、TCN实现风电预测、光伏预测、电池寿命预测、辐射源识别、交通流预测、负荷预测、股价预测、PM2.5浓度预测、电池健康状态预测、水体光学参数反演、NLOS信号识别、地铁停车精准预测、变压器故障诊断
2.图像处理方面
图像识别、图像分割、图像检测、图像隐藏、图像配准、图像拼接、图像融合、图像增强、图像压缩感知
3 路径规划方面
旅行商问题(TSP)、车辆路径问题(VRP、MVRP、CVRP、VRPTW等)、无人机三维路径规划、无人机协同、无人机编队、机器人路径规划、栅格地图路径规划、多式联运运输问题、车辆协同无人机路径规划、天线线性阵列分布优化、车间布局优化
4 无人机应用方面
无人机路径规划、无人机控制、无人机编队、无人机协同、无人机任务分配、无人机安全通信轨迹在线优化
5 无线传感器定位及布局方面
传感器部署优化、通信协议优化、路由优化、目标定位优化、Dv-Hop定位优化、Leach协议优化、WSN覆盖优化、组播优化、RSSI定位优化
6 信号处理方面
信号识别、信号加密、信号去噪、信号增强、雷达信号处理、信号水印嵌入提取、肌电信号、脑电信号、信号配时优化
7 电力系统方面
微电网优化、无功优化、配电网重构、储能配置
8 元胞自动机方面
交通流 人群疏散 病毒扩散 晶体生长
9 雷达方面
卡尔曼滤波跟踪、航迹关联、航迹融合




 ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง
ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง







