✅作者简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,matlab项目合作可私信。
🍎个人主页:Matlab科研工作室
🍊个人信条:格物致知。
更多Matlab完整代码及仿真定制内容点击👇
⛄ 内容介绍
在当今信息时代,数据的重要性日益凸显,数据预测模型成为了许多领域的关键技术。最小二乘支持向量机(Least Squares Support Vector Machine,简称LSSVM)是一种常用的数据预测方法,它通过寻找最优超平面来建立输入数据与输出数据之间的映射关系。然而,在实际应用中,LSSVM存在一些问题,如模型的泛化能力较差、计算复杂度较高等。
为了解决这些问题,研究人员提出了变模态结合秃鹰算法优化最小二乘支持向量机(Variable Mode Decomposition-based Bird-Eye-View System Optimization of Least Squares Support Vector Machine,简称VMD-BES-LSSVM)模型。该模型结合了变模态分解(Variable Mode Decomposition,简称VMD)和秃鹰算法(Bird-Eye-View System Optimization,简称BES),通过对输入数据进行分解和优化,进一步提高了LSSVM的性能。
VMD是一种信号处理技术,可以将非平稳信号分解为多个模态分量。通过VMD对输入数据进行分解,可以提取出不同的模态分量,从而更好地捕捉数据的特征。而BES算法是一种基于鸟瞰系统的优化算法,通过模拟鸟瞰系统的搜索策略,实现对LSSVM模型的参数优化。将VMD和BES相结合,可以进一步提高LSSVM模型的预测性能。
VMD-BES-LSSVM模型的实现过程如下:首先,对输入数据进行变模态分解,得到不同的模态分量。然后,利用BES算法对LSSVM模型的参数进行优化,通过搜索最优参数组合,使得模型的预测误差最小化。最后,将优化后的LSSVM模型应用于数据预测,得到准确的预测结果。
VMD-BES-LSSVM模型的优势在于多方面。首先,通过VMD分解,可以更好地提取输入数据的特征,从而增强了模型的表达能力。其次,通过BES算法的优化,可以进一步提高模型的预测性能,使得模型更加适应实际数据。此外,VMD-BES-LSSVM模型具有较好的泛化能力和计算效率,可以应用于各种数据预测问题。
然而,VMD-BES-LSSVM模型也存在一些挑战和限制。首先,模型的参数选择对结果影响较大,需要进行仔细的调参。其次,VMD-BES-LSSVM模型在处理大规模数据时的计算复杂度较高,需要考虑算法的效率。此外,模型的可解释性较差,难以直观理解模型的内部机制。
综上所述,基于变模态结合秃鹰算法优化最小二乘支持向量机VMD-BES-LSSVM实现数据预测模型(多输入单输出)是一种具有潜力的技术。通过结合VMD和BES算法,可以进一步提高LSSVM模型的预测性能,适用于各种数据预测问题。然而,在实际应用中,仍需要解决模型参数选择和计算复杂度等问题,以实现更好的性能和可解释性。随着技术的不断发展,相信VMD-BES-LSSVM模型在数据预测领域将发挥越来越重要的作用。
⛄ 部分代码
test-script for VMD authors: Dominique Zosso and Konstantin Dragomiretskiy zosso@math.ucla.edu --- http://www.math.ucla.edu/~zosso Initial release 2013-12-12 (c) 2013 When using this code, please do cite our paper: ----------------------------------------------- K. Dragomiretskiy, D. Zosso, Variational Mode Decomposition, IEEE Trans. on Signal Processing (in press) please check here for update reference: http://dx.doi.org/10.1109/TSP.2013.2288675%--------------- Preparationclear all;close all;clc;% Time Domain 0 to Tfs=400;T=60;nn=fs*T;t=1/fs:1/fs:T;freqs = ((1/T:1/T:fs)-fs/2-1/T); nn = 1000; T=1; fs = nn/T; t = (1:nn)/fs; freqs = ((1/T:1/T:fs)-fs/2-1/T); freqs = 2*pi*(t-0.5-1/nn)*T*nn;% center frequencies of componentsf_1 = 20;f_2 = 60;f_3 = 100;f_4 = 50;% modesv_1 = (cos(2*pi*f_1*t));v_2 = 1/4*(cos(2*pi*f_2*t));v_3 = 1/16*(cos(2*pi*f_3*t));v_4=1/3*(cos(2*pi*f_4*t)); for visualization purposes fsub = {}; wsub = {}; fsub{1} = v_1; fsub{2} = v_2; fsub{3} = v_3; wsub{1} = 2*pi*f_1; wsub{2} = 2*pi*f_2; wsub{3} = 2*pi*f_3;% composite signal, including noise f=csvread('17.txt',0,0,[0 0 nn-1 0]);f = v_1 + v_2 + v_3 + v_4+0.1*randn(size(v_1));f_hat = fftshift((fft(f)));% some sample parameters for VMDalpha = 2000; % moderate bandwidth constrainttau = 0.001; % noise-tolerance (no strict fidelity enforcement)K = 4; % 3 modesDC = 0; % no DC part imposedinit = 1; % initialize omegas uniformlytol = 1e-7;%--------------- Run actual VMD code[u, u_hat, omega] = VMD(f, alpha, tau, K, DC, init, tol);omega=omega*fs;%--------------- Visualization% For convenience here: Order omegas increasingly and reindex u/u_hat[~, sortIndex] = sort(omega(end,:));omega = omega(:,sortIndex);u_hat = u_hat(:,sortIndex);u = u(sortIndex,:);linestyles = {'b', 'g', 'm', 'c', 'c', 'r', 'k'};figure('Name', 'Composite input signal' );plot(t,f, 'k');set(gca, 'XLim', [0 1]);% for sub = 1:length(fsub) figure('Name', ['Input signal component ' num2str(sub)] ); plot(t,fsub{sub}, 'k'); set(gca, 'XLim', [0 1]); endfigure('Name', 'Input signal spectrum' );plot(freqs(nn/2+1:end), abs(f_hat(nn/2+1:end)), 'k'); loglog(freqs(nn/2+1:end), abs(f_hat(nn/2+1:end)), 'k'); set(gca, 'XLim', [1 nn/2]*pi*2, 'XGrid', 'on', 'YGrid', 'on', 'XMinorGrid', 'off', 'YMinorGrid', 'off'); ylims = get(gca, 'YLim'); hold on; for sub = 1:length(wsub) plot([wsub{sub} wsub{sub}], 'k--'); % loglog([wsub{sub} wsub{sub}], ylims, 'k--'); end set(gca, 'YLim', ylims);figure('Name', 'Evolution of center frequencies omega');for k=1:K plot(omega(:,k), 1:size(omega,1), linestyles{k}); semilogx(2*pi/fs*omega(:,k), 1:size(omega,1), linestyles{k}); hold on;end set(gca, 'YLim', [1,size(omega,1)]); set(gca, 'XLim', [2*pi,0.5*2*pi/fs], 'XGrid', 'on', 'XMinorGrid', 'on');figure('Name', 'Spectral decomposition');plot(freqs(nn/2+1:end), abs(f_hat(nn/2+1:end)), 'k:'); loglog(freqs(nn/2+1:end), abs(f_hat(nn/2+1:end)), 'k:'); set(gca, 'XLim', [1 nn/2]*pi*2, 'XGrid', 'on', 'YGrid', 'on', 'XMinorGrid', 'off', 'YMinorGrid', 'off');hold on;for k = 1:K plot(freqs(nn/2+1:end), abs(u_hat(nn/2+1:end,k)), linestyles{k}); loglog(freqs(nn/2+1:end), abs(u_hat(nn/2+1:end,k)), linestyles{k});end set(gca, 'YLim', ylims);for k = 1:K figure('Name', ['Reconstructed mode ' num2str(k)]); plot(t,u(k,:), linestyles{k}); hold on; if ~isempty(fsub) plot(t, fsub{min(k,length(fsub))}, 'k:'); end set(gca, 'XLim', [0 1]);end
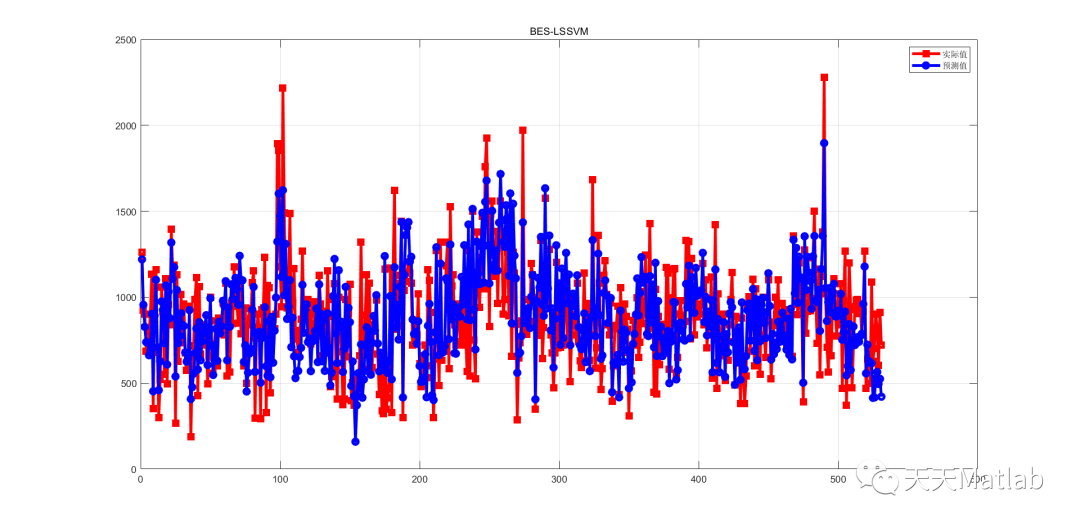
⛄ 运行结果
⛄ 参考文献
[1] 杨昭,张钢,赵俊杰,等.基于变分模态分解和改进粒子群算法优化最小二乘支持向量机的短期电价预测[J].电气技术, 2021, 22(10):6.DOI:10.3969/j.issn.1673-3800.2021.10.002.
[2] 何宝丹.基于拉曼光谱快速定量检测食用调和油含量的研究[D].燕山大学[2023-09-13].DOI:CNKI:CDMD:2.1017.726086.
❤️部分理论引用网络文献,若有侵权联系博主删除
❤️ 关注我领取海量matlab电子书和数学建模资料
🍅 私信完整代码和数据获取及论文数模仿真定制
1 各类智能优化算法改进及应用
生产调度、经济调度、装配线调度、充电优化、车间调度、发车优化、水库调度、三维装箱、物流选址、货位优化、公交排班优化、充电桩布局优化、车间布局优化、集装箱船配载优化、水泵组合优化、解医疗资源分配优化、设施布局优化、可视域基站和无人机选址优化
2 机器学习和深度学习方面
卷积神经网络(CNN)、LSTM、支持向量机(SVM)、最小二乘支持向量机(LSSVM)、极限学习机(ELM)、核极限学习机(KELM)、BP、RBF、宽度学习、DBN、RF、RBF、DELM、XGBOOST、TCN实现风电预测、光伏预测、电池寿命预测、辐射源识别、交通流预测、负荷预测、股价预测、PM2.5浓度预测、电池健康状态预测、水体光学参数反演、NLOS信号识别、地铁停车精准预测、变压器故障诊断
2.图像处理方面
图像识别、图像分割、图像检测、图像隐藏、图像配准、图像拼接、图像融合、图像增强、图像压缩感知
3 路径规划方面
旅行商问题(TSP)、车辆路径问题(VRP、MVRP、CVRP、VRPTW等)、无人机三维路径规划、无人机协同、无人机编队、机器人路径规划、栅格地图路径规划、多式联运运输问题、车辆协同无人机路径规划、天线线性阵列分布优化、车间布局优化
4 无人机应用方面
无人机路径规划、无人机控制、无人机编队、无人机协同、无人机任务分配、无人机安全通信轨迹在线优化
5 无线传感器定位及布局方面
传感器部署优化、通信协议优化、路由优化、目标定位优化、Dv-Hop定位优化、Leach协议优化、WSN覆盖优化、组播优化、RSSI定位优化
6 信号处理方面
信号识别、信号加密、信号去噪、信号增强、雷达信号处理、信号水印嵌入提取、肌电信号、脑电信号、信号配时优化
7 电力系统方面
微电网优化、无功优化、配电网重构、储能配置
8 元胞自动机方面
交通流 人群疏散 病毒扩散 晶体生长
9 雷达方面
卡尔曼滤波跟踪、航迹关联、航迹融合




 ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง
ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง





