可以取代NMS？IOU感知校准，取代NMS，成就YOLOX等目标检测更快的后处理方法

点击下方卡片，关注「集智书童」公众号

目标检测器是许多半自动和全自动决策系统的核心，它们有望变得更加不可或缺。然而，它们在可访问性方面仍然存在问题，有时可能会产生不可靠的预测。尤其令人担忧的是基本上是手工设计的非极大值抑制（NMS）算法，这些算法导致了一个复杂的预测过程和有偏的置信度估计。

作者展示了通过使用IoU感知校准，可以消除经典的NMS风格的后处理。IoU感知校准是一种条件Beta校准；这使得它可以并行处理，而且没有超参数。与任意的截止值或折扣相比，它隐含地考虑了每个检测被视为重复的可能性，并相应地调整置信度分数，从而为每个检测提供了基于经验的精度估计。

作者在不同的检测架构上进行了广泛的实验，结果表明所提出的IoU感知校准可以成功地对重复检测进行建模并改善校准。与标准的顺序NMS和校准方法相比，作者的联合建模可以在比最佳的基于NMS的替代方法更少的复杂性的情况下提供性能提升，同时产生一致性更好的校准置信度预测。

1、简介

目标检测器在当今许多领域中都是不可或缺的，包括计算机视觉、机器人技术和自动化系统。它们能够在图像或视频中定位和识别目标，实现目标识别、跟踪和场景理解。目标检测器还是最近驾驶辅助系统、监视系统和增强现实领域取得的重要进展的核心。随着安全、工业自动化甚至零售等领域对先进技术的需求不断增加，目标检测器在未来将发挥更加重要的作用。

目标检测器的普及似乎不可避免，但仍然存在一些障碍。用户可能会包括更多的非专家，因此透明度和可访问性——在今天的检测器中仍然存在问题——将是至关重要的。检测器还需要具有可靠性和可解释性，因为大规模部署可能会放大现有的问题和偏见。研究人员和实践者需要仔细检查当前的目标检测流程，并解决它们在可靠性、可解释性和偏见这些关键领域的不足之处。

几乎所有目标检测器后处理流程中特别麻烦的部分是非极大值抑制（NMS）。这是一个手工设计的算法，旨在减少对同一个目标的重复检测。为了使NMS能够正常工作，设计人员需要定义一个特定的阈值，该阈值控制了当它们重叠时哪些检测被视为冗余。Soft-NMS——传统NMS算法上最流行的改进——引入了一个不同的超参数，通过高斯分布确定了重叠检测的置信度分数的折扣程度。这个相当难以理解的超参数可能会对性能和可靠性产生很大的影响，需要谨慎选择。

在另一个领域中使用一个为某个用例设计的算法，甚至只是对频繁领域转移进行适应，可能会很麻烦。这需要对目标领域有所了解，了解所用NMS算法参数的工作原理以及它们如何影响检测器的预测。或者，可以搜索参数空间以找到最大化性能的设置，但这仍然会让用户对它们的影响缺乏甚至是表面的了解。

精确的概率评估对于自动决策至关重要，确保准确可靠的结果和适当的风险评估。NMS引入的不连续性以及Soft-NMS的置信度折扣扭曲了本应反映准确概率的检测置信度分布。已经证明NMS会影响置信度预测的校准，而这些置信度预测通常已经存在初始误校准。当置信度值不反映目标存在的经验概率时，它们会变成对不同检测之间的相对可能性排名的难以理解的排名，这对于自动系统来说基本上是无用的。

作者建议将去除重复检测问题映射到置信度分数中，作为一个统一的决策标准，采用作者的数据驱动的IoU感知校准。作者展示了作者提出的IoU感知校准可以隐式地考虑到每个检测是否是另一个检测的重复，并产生经过良好校准的置信度估计，从而消除了对其他后处理步骤（如NMS和“正常”置信度校准）的需求。

IoU感知校准具有以下几个优点：

1. 它是一种黑盒校准方法，即可以作为后处理应用于任何目标检测器
2. 它通过隐式建模重复检测的概率来共同解决了NMS和置信度校准问题，使NMS变得不再必要，并产生更可靠的置信度预测
3. 它可以矢量化，因为它不需要Soft-NMS和 Greedy-NMS的迭代计算
4. 它没有需要手动调整的超参数
5. 它在广泛测试的多种检测器上与最佳NMS相比产生了类似或更好的性能，并且具有更好的校准

2、背景

目标检测器几乎总是使用检测建议与GT目标的多对一分配进行训练。这种方法提高了检测性能，因为它可以减轻检测器的前景-背景类别不平衡问题——每个图像中都有无数个非目标，只有有限数量的可检测目标。这种训练策略在定义上激励每个目标产生多次检测。然后需要在推断过程中过滤掉这些多余的检测。

2.1 非极大值抑制

通常，决定保留哪些检测结果和哪些丢弃的组合优化问题仍然是使用NMS或soft-NMS来解决的（见算法1）。

Soft-NMS和标准的NMS算法都依赖于这样一个前提，即重复的检测被认为具有相似的尺度并且高度重叠。这两个检测和的“接近程度”是通过它们各自边界框和的Jaccard指数来量化的，也称为它们的重叠率（IoU）：

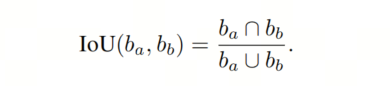
请不要与Jaccard距离混淆，Jaccard距离是。第二个共享的假设是，更高的预测置信度表示检测成为真正阳性（TP）检测的可能性高于检测。因此，这两个算法都从最高到最低的置信度中贪心地评估所有N个检测结果D。在检测时，根据以下方式更新置信度：

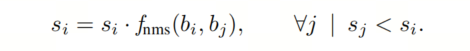
NMS使用一个任意定义的锐利截止阈值来将检测结果分类为更自信的检测结果的重复，并完全削减它们：

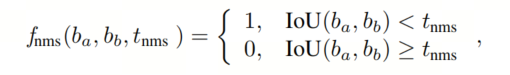
而soft-NMS只根据它们的重叠程度折扣重叠检测的置信度，通常使用高斯函数：

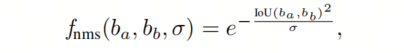
具有单独的超参数σ。它是根据这样一个假设设计的，即具有更自信的重叠检测仍然可以成为TP检测，只是成为TP检测的可能性较低。

2.2 目标检测器校准

假设一个模型使用其检测的置信度、边界框和类别来预测目标的存在。如果始终等于它成为TP检测（τ）的概率（即在的情况下其精度为1），则模型被校准了：

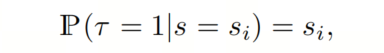
对于任何。在目标检测设置中，TP检测的概念比分类设置中更加复杂，分类设置只要求预测的类别与GT标签匹配。为了评估检测为TP（τ），需要将其具有正确类别和边界框的所有检测D的集合中具有最高置信度的检测，且该边界框与GT目标有足够的重叠。

重叠的充分程度根据IoU的阈值（与GT目标的IoU）确定。这为TP检测的概念引入了一些模糊性，即的“好”值是多少。在性能评估指标mAP中，通过在IoU阈值 ∈ [0.5, 0.55, …, 0.95]的范围内评估来解决这个问题。通常需要二进制标签进行置信度校准，因此，除非另有规定，作者使用 = 0.5，与mAP50相同。

2.2.1 测量校准误差

期望校准误差（ECE）试图捕捉在某些数据分布和整个置信度区间上的方程（5）的左右两侧的预期差异。为了使这种评估实际可行，采用了某些简化方法。置信度可以在区间[0,1]上取任何值，并且必须通过将区间分割为固定数量（B），通常为B=10的bin 来离散化，每个bin b包含nb个检测。每个bin的精度τ在带标签的保留集上对N个检测进行评估。结果可以在可靠性图中可视化，或者平均以产生检测ECE度量[14, 22]：

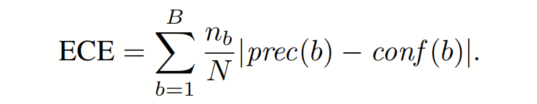
标准ECE已被证明存在许多病态。为了解决这个问题，Nixon等人引入了ECE的两个变体。静态校准误差（SCE）旨在通过分别计算每个类别的ECE，然后平均结果来解决类别依赖性问题。第二个指标，自适应校准误差（ACE），使用自适应分箱方案。目标检测器的置信度通常不均匀分布，而是更密集地聚集在接近0和1的极端值附近。为了考虑这种不平衡，ACE使用间隔的bin，因此每个bin包含大约相同数量的检测。在本工作中，所有校准度量，即ECE、ACE和SCE，除非另有说明，均以百分比表示。

通常，负对数似然（NLL）等适当的评分规则被用于拟合和验证校准方法。只有当没有校准错误时，NLL才能最小化，但它不直接捕捉校准错误。

2.2.2 置信度校准

现代神经网络通常没有很好地校准，现代基于深度学习的目标检测器也没有。模型不可知（黑盒）置信度校准的目标是调整由统计模型产生的置信度估计，以更好地反映使用某些映射的实际预测结果的概率，该映射受概率分布启发。在目标检测的背景下：

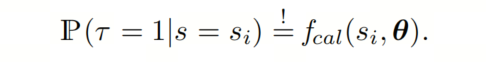
根据这个符号，校准函数是用θ参数化的。还有一些非参数校准函数，如直方图分bin、等渗回归和贝叶斯分bin，作者这里省略了，因为它们在多变量校准设置中存在一些独特的问题。常见的参数化校准方法包括Platt缩放、Beta校准和温度缩放。

请注意，大多数参数化校准函数是针对对数输出而不是作者出于简化而使用的最终置信度值定义的，但可以进行转换。

校准函数的参数不能直接优化在其定义的目标上，如方程（7）所示。它们是根据一些评分规则进行优化的，如负对数似然损失或Brier分数，从而产生一个优化标准，如：

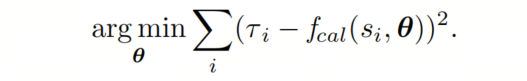
以这种形式，校准可以被视为对逻辑回归问题的优化，并可以使用基于梯度的优化程序来解决。

2.2.3 多变量置信度校准

置信度校准可以进一步扩展到建模双或多变量概率分布，以将它们应用于多输出模型。目标检测器产生额外的回归输出，即它们的边界框预测，可以用于多变量校准。例如，目标检测器的多变量校准的目标是：

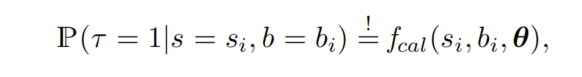
其动机是消除与目标位置或大小有关的任何条件置信度偏差。多变量校准函数可以从其单变量对应物中导出。如果作者将条件变量——在这种情况下是和——视为彼此独立，那么校准函数的修改就是其单变量对应物的一个相对简单的矢量化版本。

当作者合理地假设变量相互依赖时，作者还需要对协方差矩阵进行建模。作者使用Kuppers等人的实现，他们在其多变量校准框架中为目标检测器引入了适用于逻辑和Beta校准的有条件依赖和独立多变量适应。

与单变量校准不同，如果关于附加模型输出存在任何条件偏差，多变量置信度校准可能会影响模型的性能。

3. 基于IoU的校准

目标检测器是自动决策系统中视觉堆栈的一个重要组成部分。为了确保对这些系统的信任，目标检测器可靠地产生带有精确概率估计的预测至关重要。这些预测的可靠性对于做出明智决策并在自动化系统中实现可靠结果至关重要。

与这一目标形成鲜明对比的是，普遍采用的多对一检测到目标分配范式——在较小程度上，采用一对一分配——使检测器为单个目标生成重叠的重复检测。这些自信的重复检测可以严重影响检测器的性能，因此通常会被丢弃或根据它们与启发式算法中的其他检测的重叠程度进行严重折扣。

作者认为，如果预测的置信度恰当地考虑了检测为重复的可能性，作者可以完全消除NMS后处理。因为可能为重复的检测的置信度会非常低，反映了它们为真实检测的总体概率很低。因此，作者的目标是开发一种数据驱动的方法，产生透明的决策标准，以提高目标检测的准确性和可靠性。这种方法必须确保适当估计了重叠检测的实际重复概率，从而产生经过良好校准的可靠置信度预测。

如果作者允许在大多数NMS方法的隐含假设下，那么检测为重复的概率δ依赖于其置信度以及与同一类别的所有其他检测的IoU，作者通过Jaccard距离向量表示，即。

如果作者想要在Eq.（5）的校准定义中包含明确计算的概率，即检测不是重复的条件概率δ和非重复检测为正确，即TP检测（τδ）的概率，结果为：

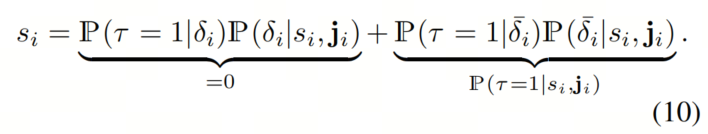
这要求作者明确确定检测不是重复的条件概率δ和非重复检测为正确，即TP检测的条件概率（τδ）。作者可以通过经验确定τ，从而跳过明确计算非重复概率的步骤。这种方法将问题转化为双变量置信度校准（如Eq.（9）中定义）。

条件引起了一个实际问题，因为它不是一个单一的参数，而是一个随检测数量变化的向量。NMS方法通过迭代处理所有具有更高置信度的框对的Box来解决这个问题（参见Eq.（2）），但作者也可以使用Jaccard距离的基本摘要统计数据，类似于Matrix Non-Maximum Suppression提出的方法。这些摘要统计数据可以在所有检测之间的（1 – IoU）值的Jaccard距离矩阵上并行计算：

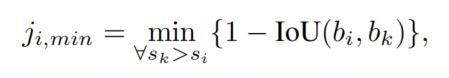
从而消除了NMS算法的复杂度中的串行计算需求，该算法适用于N个检测。作者将使用作为ji的代理，除非另有说明（请参见Sec. 5.1中的相关内容）。根据这些设计选择，作者的优化目标变为：

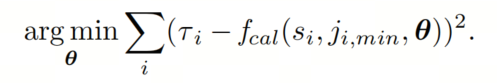
对于校准函数，作者选择双变量条件Beta校准，因为它比Logistic校准更具表现力；它在模型的预测已经进行了良好校准时会产生恒等函数，代价是需要更多的参数。作者假设作者的重叠代理（）与置信度之间存在条件依赖关系，因为作者仅从更有信心的检测中计算最小的Jaccard距离，即在经典NMS设置中“抑制”检测的那些检测。这已经引入了两个变量之间的间接依赖性，作者希望在建模中考虑到这一点，但作者也将取消此选择。

通过这种方法，作者现在可以根据Jaccard距离与其他检测之间的摘要统计数据来调整检测，从而隐式地考虑了每个检测为重复的概率。这应该有助于目标检测器可靠地产生带有精确概率估计的预测，并消除NMS后处理的需要。

4、实验

初步结果

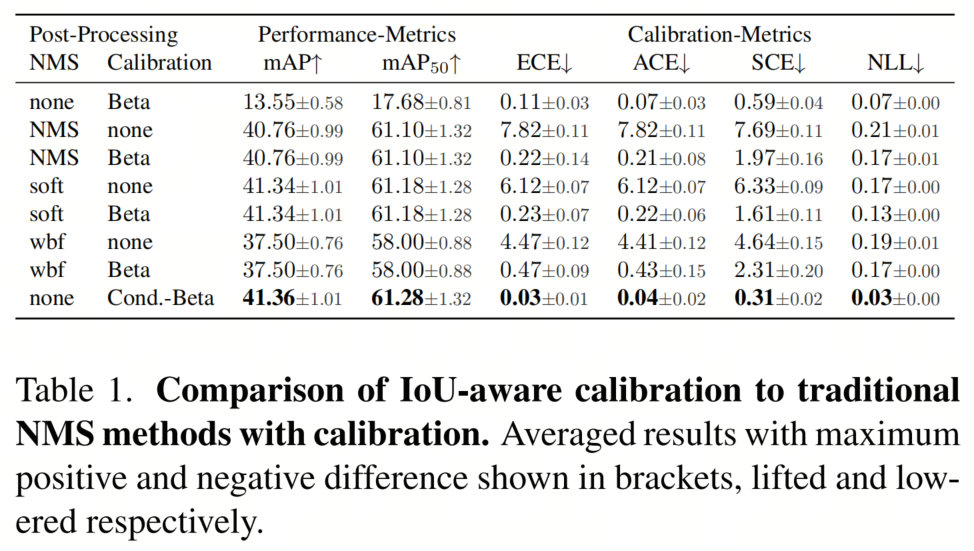
结果如表1所示。正如预期的那样IoU感知校准产生了经过良好校准的检测结果。与最佳校准的NMS结果相比，显著的改进表明，隐式建模重复检测的概率确实是产生精确概率估计的关键必要条件。IoU感知校准在性能指标上表现得非常出色。

在这种情况下，它甚至优于最佳的NMS，即Soft-NMS稍微领先NMS 0.6 mAP。这尤其令人惊讶，因为作者的方法仅依赖于与最重叠的其他检测之间的Jaccard距离。相比之下，迭代NMS方法考虑了它们的迭代方法中所有重叠的检测。

IoU感知校准的作用是什么？

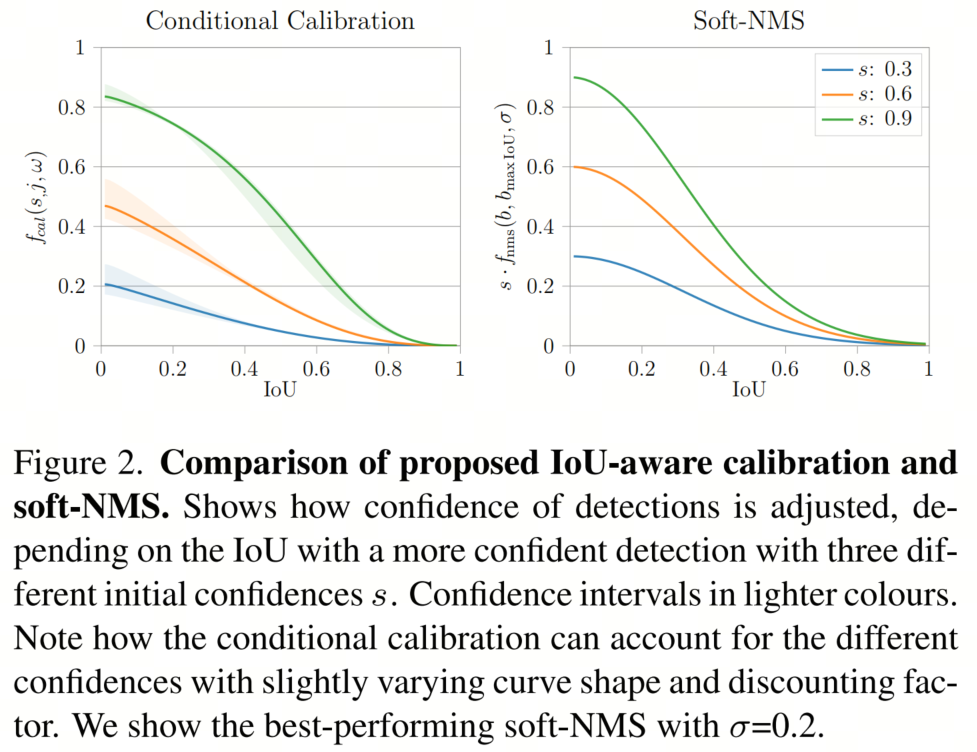
受到优秀的结果启发，作者检查了学到的fcal的作用（见图2左）并将其与高斯Soft-NMS进行了比较（见图2右）。IoU感知校准不仅通过重叠量（在IoU中）来调整置信度映射的形状，还通过初始置信度值来调整。虽然对于s=0.9，曲线近似于高斯，但对于s=0.3，它更像线性衰减。

与Soft-NMS相比，高IoU的置信度折扣也大大减少，特别是对于初始高置信度值。Soft-NMS是迭代应用的（参见Eq.（2）），对于每个更有信心的检测，因此具有多个重叠的更高信心的检测将更大幅度地降低其置信度。

消融实验

作者的IoU感知校准取得了良好的结果，这表明作者的设计和建模选择是有根据的，准确反映了潜在问题。尽管如此，作者通过剔除实验来评估每个建模选择的影响并确认其有效性。

校准函数的选择

作者选择了Beta校准函数而不是Logistic函数，因为它更具表现力。作者假设检测的置信度与作者的更高置信度检测的重叠代理之间存在条件依赖关系。图2的视觉检查确认了学到的模型在两个变量之间的某种交互作用。作者将有条件的双变量Beta校准与独立版本以及有条件和独立的双变量Logistic校准函数进行比较。

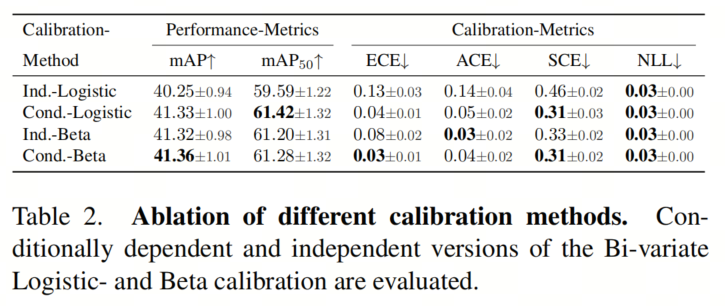
如表2所示，校准函数之间没有显著差异，除了独立的Logistic校准，它在性能和校准指标方面表现明显较差。独立的Beta校准的ECE仅比其有条件的对应物稍高。有条件Logistic和Beta校准之间的性能差异很小。作者在实验中使用Beta校准，但请注意，有条件的Logistic校准可能会产生类似的结果。

根据其他汇总统计条件

作者选择了通过取最小的Jaccard距离，即最大的IoU，来获得汇总统计的。Greedy-NMS方法通过迭代应用置信度调整，从而考虑了重叠的个体检测，而不仅仅是极值。这种方法不能转移到作者的校准方法，但作者可以寻找一个汇总统计，以解决其他重叠检测的问题。理想情况下，该值应该在[0,1]范围内，使Jaccard距离的乘积成为理想选择。

作者将结果变量表示为。作者计算和从ji计算，对于所有具有比其调整置信度更高的检测，其有信心的检测，其置信度得以调整。在NMS的背景下，这些将是与抑制边界框重叠的边界框；这将留下未考虑的检测对检测进行抑制的潜在影响。

为了解决这个问题，作者还可以为的剩余部分计算所提出的汇总统计，即和，尽管作者没有先验理由认为这些统计数据与作者的校准目标相关。

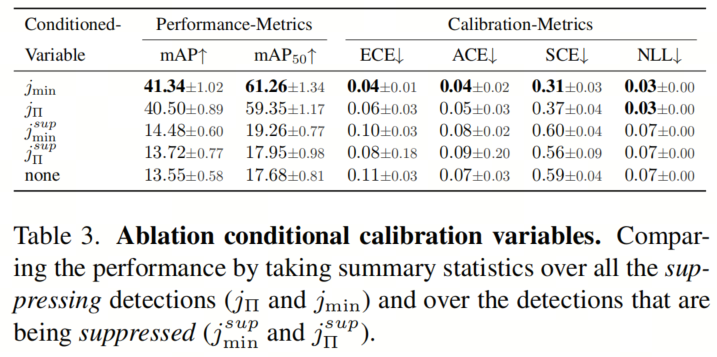
通过比较不同变量的条件（见表3），作者发现以jmin为条件的性能和校准分数明显更好，而其他选择则没有明显差异。引入的乘积在捕获重复检测的可能性方面效果不佳，而受抑制检测的统计数据和几乎与基线相比略微好一些，这可以从性能指标中看出。

根据其他变量进行条件编码

到目前为止，作者仅对置信度s和所有Jaccard距离到其他检测的单个汇总统计（）执行了双变量校准。虽然其他提出的指标单独表现不佳，但作者可以将它们与最佳统计信息组合成多变量置信度校准，以查看它们是否共同更能够模拟重复的可能性。作者探索了所有其他可用的汇总统计信息，即、和与和s的所有可能组合（见表4）。

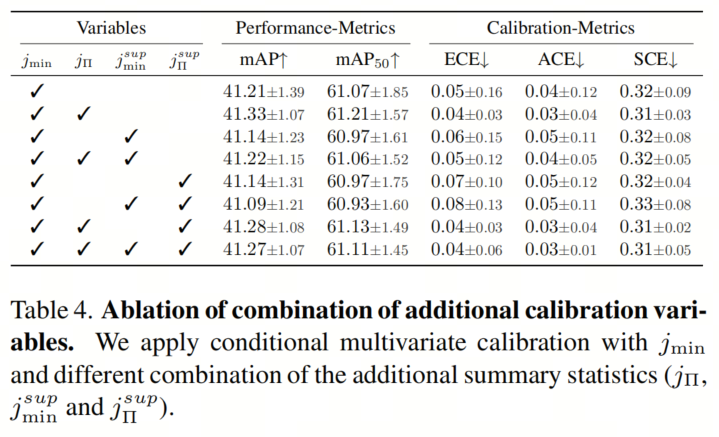
从性能和校准指标中可以看出，没有明显的改进。包括的组合似乎比不包括jΠ的组合稍好一些。但与有条件的贡献不同，这些收益远远不足以证明对其他变量进行条件建模是有必要的。

实验结果

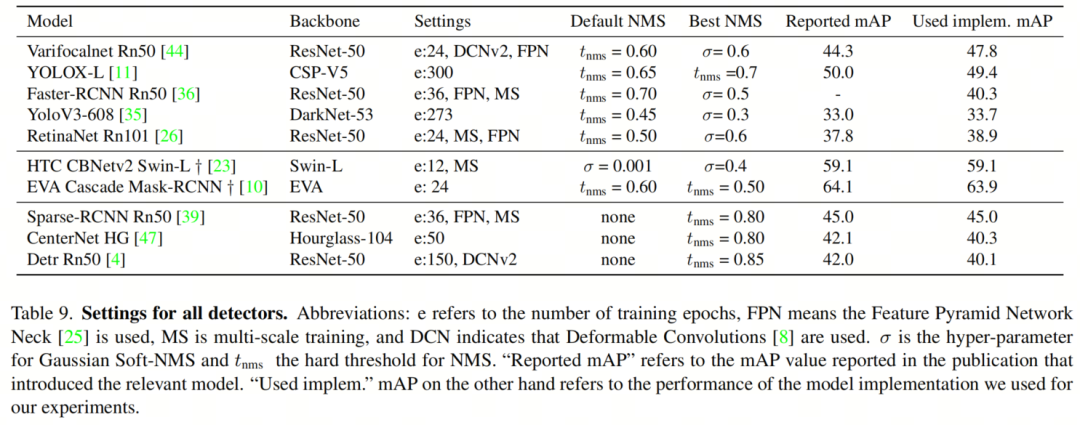
最后，作者在各种不同的目标检测架构上验证了作者的IoU感知校准的有效性。作者旨在代表不同的设计理念：从单阶段到两阶段，从小型实时模型到巨大的百亿参数模型，基于锚点和无锚点，设计用于NMS或不使用NMS后处理，基于Transformer和基于CNN的模型以及不同的Backbone网络。

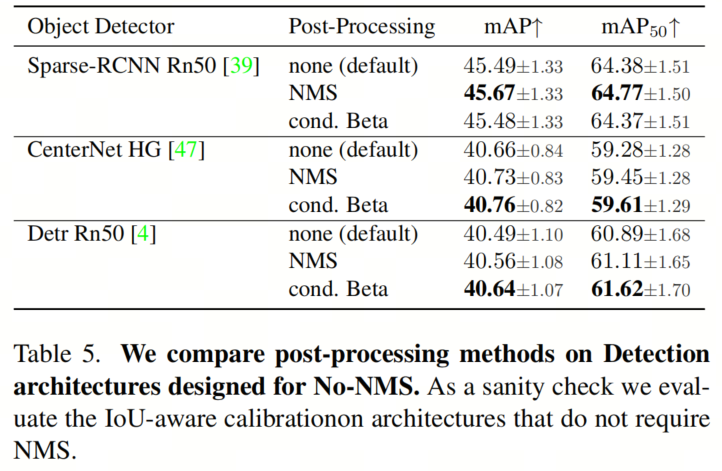
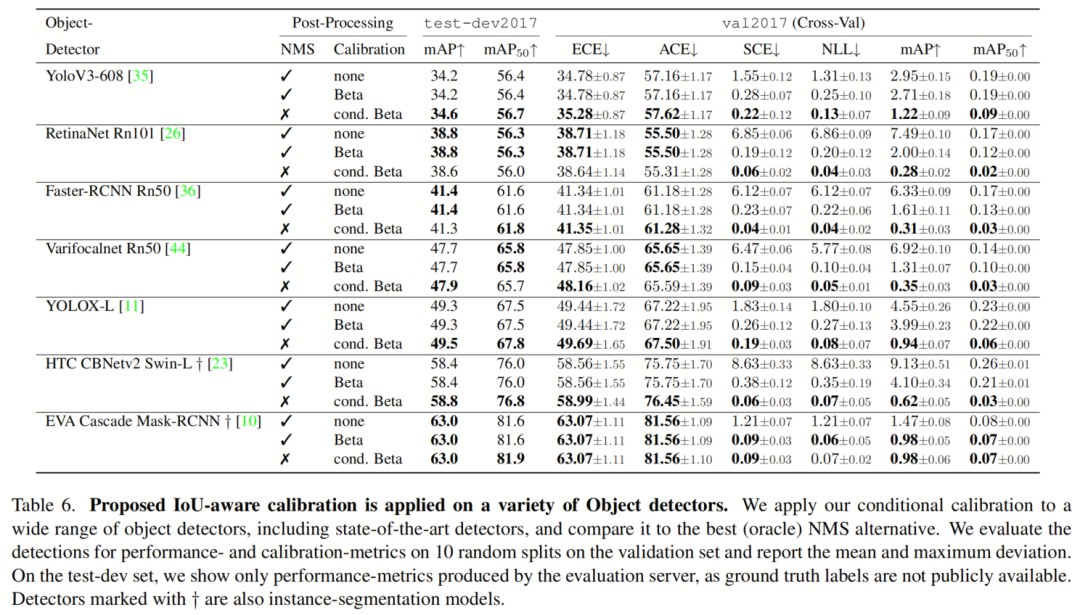
所有目标检测器的结果如表6所示。作为一种合理性检查，作者还验证了在没有NMS后处理的架构上的性能变化很小（见表5）。该方法始终优于标准的NMS，对于某些模型，性能提高了高达0.7 mAP，并且通常可以改进优化调整的Soft-NMS高达0.4 mAP。

5.讨论

IoU感知校准的性能与最佳微调的NMS方法相当，这证明了它能够模拟重复检测的潜在问题，而不考虑架构，比任何类型的NMS更好。更好校准的置信度预测进一步表明，校准不仅能够隐含地捕捉到重复的可能性，而且重复的可能性还是准确反映经验精度的关键中介。这表明作者可以将去重融入校准中，以简化后处理并减少复杂性，从而改善校准和性能。

局限性

IoU感知校准是一种数据驱动方法，因此在用于校准的数据和部署时看到的数据之间存在分布变化可能会导致过于自信或不自信的预测。在比校准子集中拥挤得多的场景中，还可能导致性能下降。

6. 参考

[1]. Do We Still Need Non-Maximum Suppression? Accurate Confidence Estimates and Implicit Duplication Modeling with IoU-Aware Calibration.

7. 推荐阅读

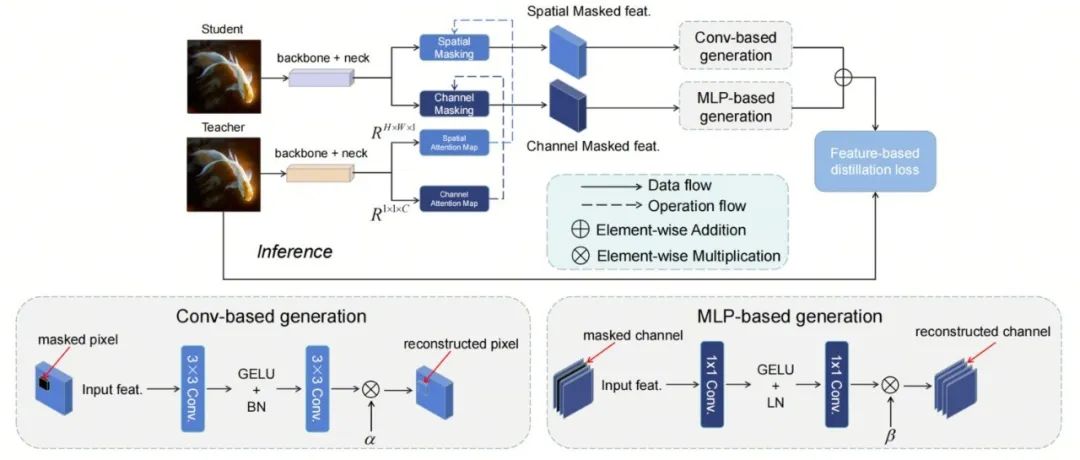
DMKD蒸馏 | 模型学习，空间/通道信息我都要！超越FKD、FGD、MGD以及AMD方法！

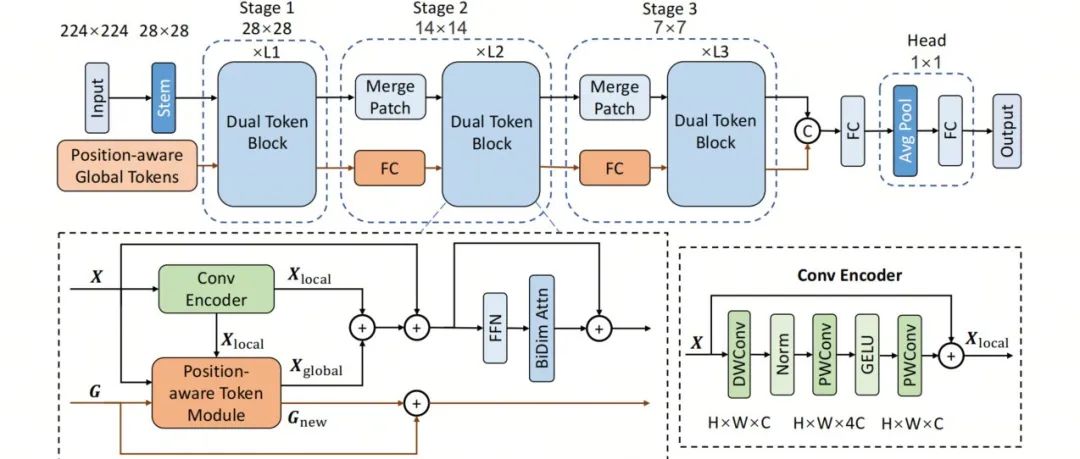
DualToken-ViT | 超越LightViT和MobileNet v2，实现更强更快更轻量化的Backbone

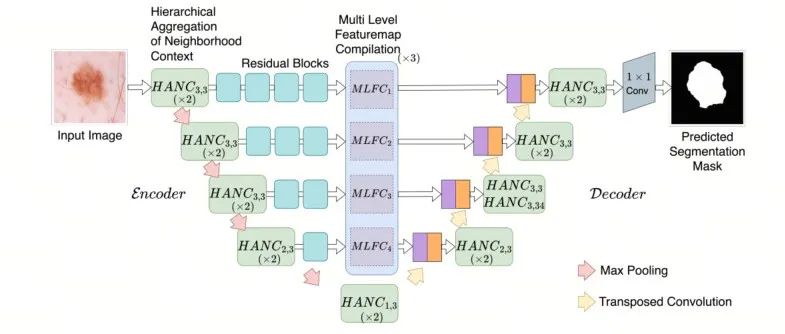
ACC-UNet | 致敬ConvNeXt，全卷积结构UNet设计，超越SWin-UNet！

扫码加入👉「集智书童」交流群

（备注：方向+学校/公司+昵称）

想要了解更多：

前沿AI视觉感知全栈知识👉「分类、检测、分割、关键点、车道线检测、3D视觉（分割、检测）、多模态、目标跟踪、NerF」

行业技术方案👉「AI安防、AI医疗、AI自动驾驶」AI模型部署落地实战👉「CUDA、TensorRT、NCNN、OpenVINO、MNN、ONNXRuntime以及地平线框架」

欢迎扫描上方二维码，加入「集智书童-知识星球」，日常分享论文、学习笔记、问题解决方案、部署方案以及全栈式答疑，期待交流！

免责声明凡本公众号注明“来源：XXX（非集智书童）”的作品，均转载自其它媒体，版权归原作者所有，如有侵权请联系我们删除，谢谢。
点击下方“阅读原文”，了解更多AI学习路上的「武功秘籍」