
高维展开是图展开到高阶边的推广,最近在理论计算机科学界引起了极大的关注,因为它们在纠错和近似采样等应用中提供了额外的推动力。在本论文中,我们利用多项式几何和高维凸几何的工具,探讨了与高维展开相关的两个问题。
首先,我们研究离散分布的近似采样。从高维展开获得的采样框架既提供了一组用于 MCMC 算法的自然随机游走,也提供了一组用于分析的工具。我们证明,从分布导出的多项式的几何特性(例如对数凹性)使我们能够加速这些随机游走的实现。
接下来,我们研究一种称为“随机几何图”的随机图模型,最终目标是了解其建模能力及其高维展开特性。在此过程中,我们证明了区分随机几何图模型与 Erdós-R´enyi 模型的新结果,并开发了一个新的几何工具包来分析这些图。

论文题目:Geometry-Inspired Sampling Algorithms and Random Graphs
作者:Elizabeth Yang
类型:2023年博士论文
学校:University of California, Berkeley(美国加州大学伯克利分校)
下载链接:
链接: https://pan.baidu.com/s/1P89aFFhTtUnMVO9iYVNXjQ?pwd=buxt
硕博论文汇总:
链接: https://pan.baidu.com/s/1Gv3R58pgUfHPu4PYFhCSJw?pwd=svp5
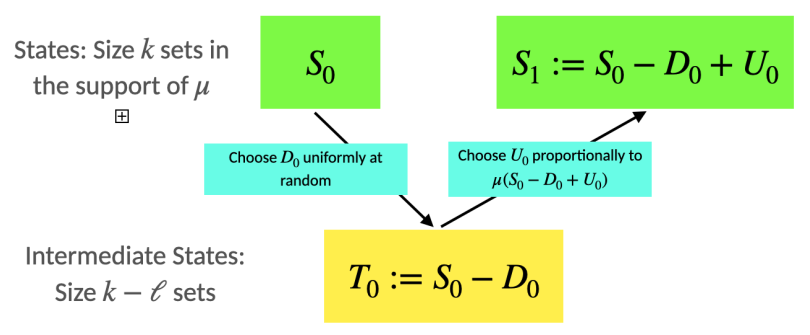
该图说明了自下而上行走的单个步骤。
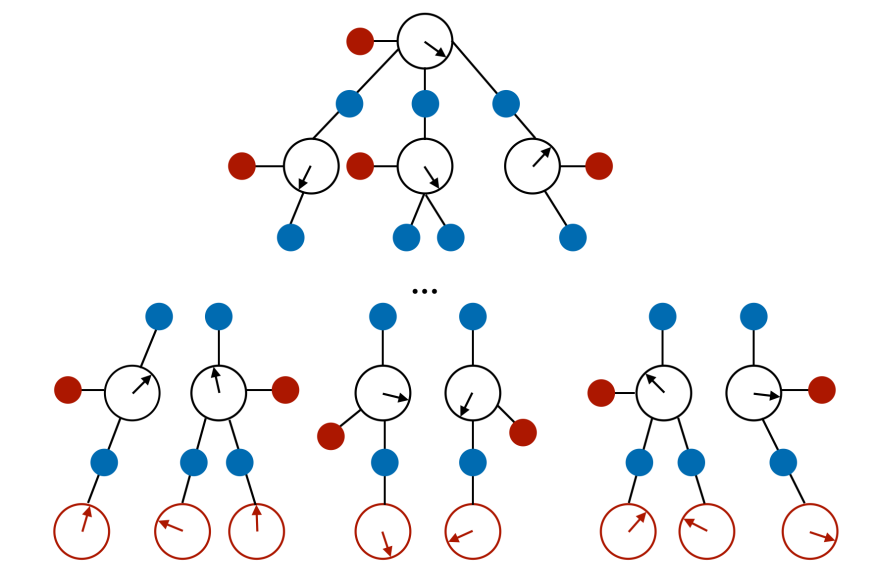
没有非边约束的因子图。这里,所有带箭头的圆圈代表变量节点,实心圆圈代表网络约束节点。红色变量代表固定向量。红色实心圆圈是一元约束(对固定向量的非边缘约束),而蓝色实心圆圈是边缘约束。



微信群 公众号






 ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง
ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง







