MIT｜非线性复杂度理解领悟（grokking）即压缩

​

Grokking as Compression: A Nonlinear Complexity Perspective

Z Liu, Z Zhong, M Tegmark
[MIT]

非线性复杂度理解领悟(grokking)即压缩

要点:

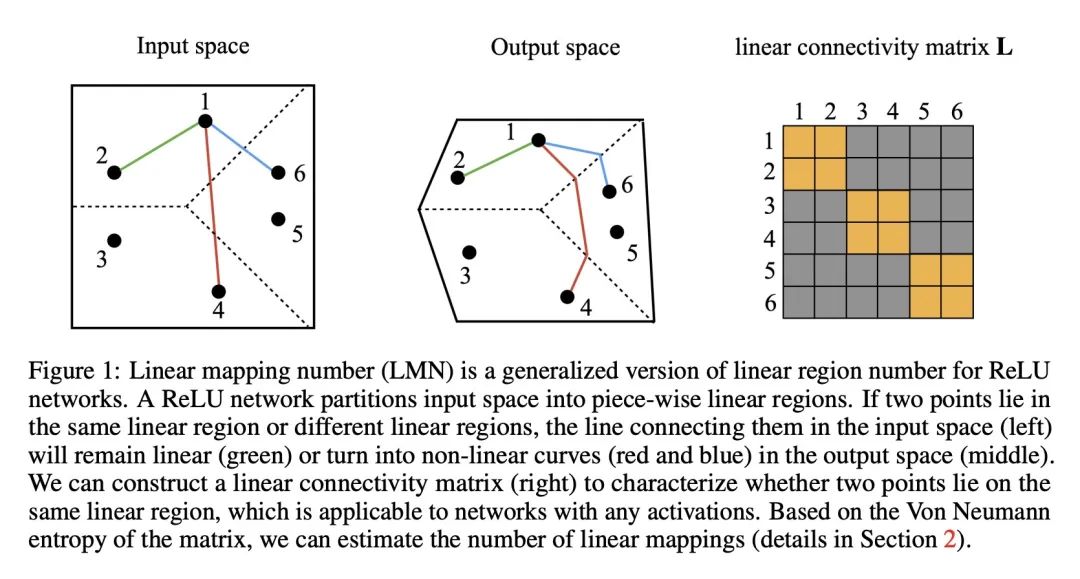
• 本文提出一个叫做线性映射数(LMN)的新指标，用来测量神经网络的复杂度，LMN把ReLU网络的线性区域数的概念推广到任意激活函数的网络。
• LMN可以看作是网络的信息量或可压缩性的度量，它测量用于逼近网络函数所需的线性映射的个数。
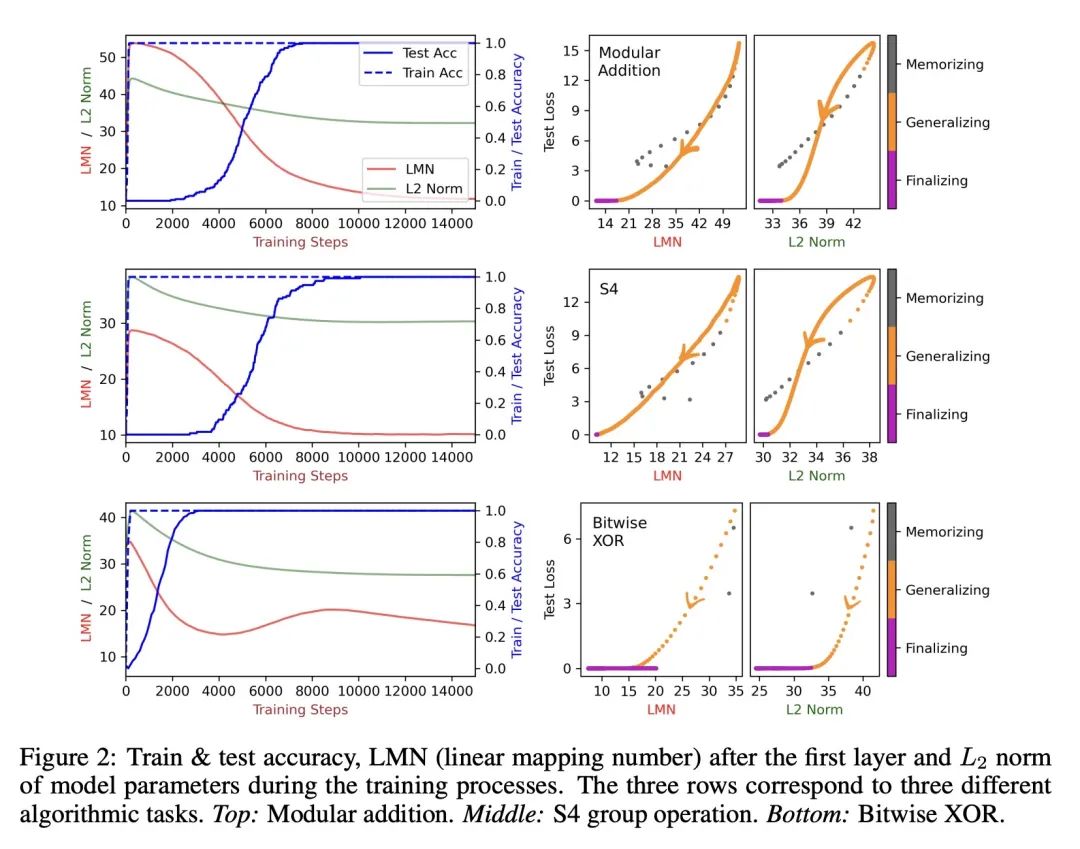
• 本文认为与L2范数相比，LMN更好地刻画了“领悟(grokking)”现象，即记忆之后泛化延迟出现，在记忆和泛化之间的时期内，LMN持续下降，反映了压缩过程。
• 与L2范数相比，LMN与测试损失之间具有更简单的线性关系，LMN还揭示了L2范数未捕捉到的多位XOR的有趣双降现象。
• 本文认为LMN可能是Kolmogorov复杂度的神经网络版本的有希望候选，因为它明确考虑了与现代神经网络结构相符的局部线性计算。

动机：解释“领悟(grokking)”现象(即记忆后的泛化延迟)的原因，并提出一个衡量神经网络复杂性的度量方法。

方法：提出一种称为线性映射数(LMN)的度量方法，用于衡量网络(或子网络)的复杂性。LMN是ReLU网络线性区域数的推广版本，并且可以适用于具有平滑激活函数的网络。

优势：与已有的用于衡量网络复杂性的L2范数相比，LMN在多个方面具有优势：(1)LMN可以自然地解释为信息/计算复杂性，而L2无法做到；(2)在压缩阶段，LMN与测试损失之间存在良好的线性关系，而L2与测试损失之间存在复杂的非线性关系；(3)LMN还揭示了XOR网络在两个泛化解之间切换的有趣现象，而L2则没有。此外，LMN也被认为是神经网络版本的科尔莫哥洛夫复杂性的有希望的候选方法。

提出一种衡量神经网络复杂性的度量方法LMN，通过解释grokking现象来展示其优势，突出了与L2范数的不同和XOR网络的反直觉结果。

https://arxiv.org/abs/2310.05918 

​Read More