GPT-4野生代言人陶哲轩：搞论文学新工具没它得崩溃！11页“超简短”新作已上线

丰色 发自 凹非寺
量子位 | 公众号 QbitAI

陶哲轩有多爱GPT-4？

这回，不止写论文做研究，学新工具时他也离不开它了。

就在今天，他的又一篇成果上线，关于麦克劳林不等式。

为了更好地展现其成果，48岁的他开始学习Lean4（一种可作为交互式定理证明工具的函数式编程语言）。

他自述，随着学习该语言“关卡难度”的增加，GPT-4又能帮大忙了——

如果没有它帮我解决各种微妙的语法问题，你都无法想象我有多崩溃。

不愧是GPT-4的“野生代言人”。

至于这次的论文，陶哲轩表示：

非常简短，只有11页。并且用到的方法非常基础，只需要本科的微积分和多项式知识就可以。

一起来看看

麦克劳林不等式

这篇论文10月10日发表，距离上一篇“欧拉函数的单调非递减序列”差不多正好一个月。

总的来说，这篇论文主要讲的是经典麦克劳林不等式认为初等对称为以下形式（公式1）：

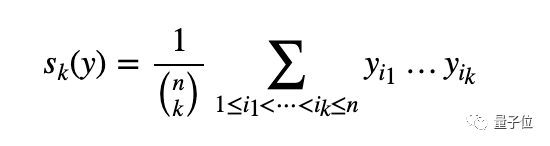
当1≤k≤ℓ≤n且y=(y1,…,yn)由非负实数组成时，它服从不等式（公式2）：

在此，陶哲轩提出了一个变体（公式3）：

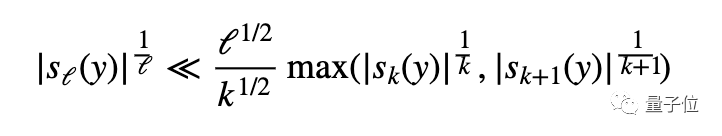
在这个变体中，yi被允许为负。

在这种情况下，不等式“急剧上升”为常数，即使分母不含k1/2因子不等式也是已知的。

具体而言，陶哲轩写道：

公式2也可以被用牛顿不等式来证明：

所有1≤k<n和任意实数y1,…,yn有效（特别是这里的yi被允许为负数。</n和任意实数y1,…,yn有效（特别是这里的y

但是请注意，当k=1，n=2时，它就是算术平均-几何平均不等式了：

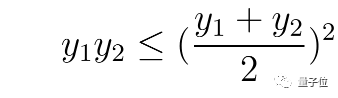
这种不等式的一般情况可以通过许多标准操作从上面这种特殊情况中推导出来。

为什么可以？这主要归功于罗尔定理（Rolle’s theorem）。

但陶哲轩指出，关键点是是该运算保留了直到Sn-1为止的所有基本对称均值。

接下来，我们可以将麦克劳林不等式视为提供n变量上的算术平均-几何平均不等式的改进版本（当k=1，ℓ=n时）。

不过，牛顿不等式适用于任意实数yi ，一旦允许一个或多个yi为负，麦克劳林不等式就会“崩溃”。

但鉴于当n为偶数时会出现一个关键示例：yi的一半等于+1，一半等于-1。

我们就可以验证基本对称均值sk中当k奇数时“消失”，为偶数时则等于：

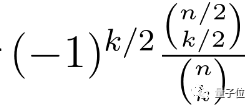
特别地，一些常规估计可以得出量级界限（公式a）：

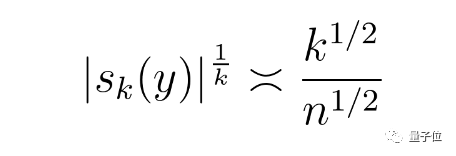
问题又来了，由于当0<k≤n上式也成立，因此即使在sk(y)上加上绝对值之后仍然严重违反了麦克劳林不等式。</k≤n上式也成立，因此即使在s

另一方面，其他数学家还观察到，如果两个连续值都很小，这会导致所有后续值sℓ(y)也很小。

还有另一数学家观察到了这一说法的更精确版本（公式b）：

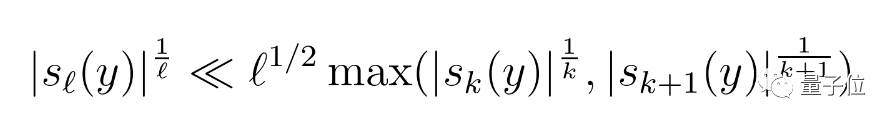
其中1≤k≤ℓ≤n且y=(y1,…,yn)为实数（但可能为负）。

假设k=1，ℓ=n，我们就能得到不等式：

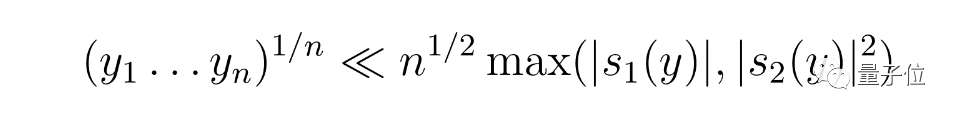
再结合算术平均数-几何平均数不等式又可以成立不等式：

以及等式：

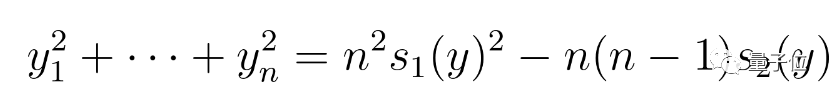
与牛顿不等式的证明一样，公式b的一般情况可以通过一些标准操作（包括前面提到的微分运算）从这个特殊情况得到。

然而，如果对照关键示例给出的边界a (公式a) 检查边界n (公式b)，我们会发现不匹配：

在k1/2的影响下，b的右侧比左侧大。

在此，论文的主要成果就是通过建立最佳修改（直至常数），即前面提到的公式3来纠正这一问题。

这个成果也回答了数学网站MathOverflow上网友提出的疑问：

那么陶哲轩是如何解决的呢？

与前面的论点不同，他在这里不主要依赖算术平均数-几何平均数不等式。相反，主要工具是新的不等式：

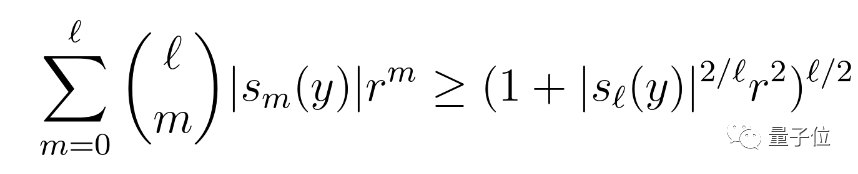
它对所有1≤ℓ≤n和r>0有效。

该式子的证明大家如果感兴趣可以进一步查阅博客或论文，主要涉及一些微积分、二项式定理和多项式的知识。

论文地址：
https://arxiv.org/abs/2310.05328 

参考链接：
https://terrytao.wordpress.com/2023/10/10/a-maclaurin-type-inequality/（博客） 
https://mathstodon.xyz/@tao

— 完 —

「量子位2023人工智能年度评选」开始啦！

今年，量子位2023人工智能年度评选从企业、人物、产品/解决方案三大维度设立了5类奖项！欢迎扫码报名 

MEET 2024大会已启动！点此了解详情。

点这里👇关注我，记得标星哦～

一键三连「分享」、「点赞」和「在看」

科技前沿进展日日相见 ~