
关键词:博弈论,博弈动力学,纳什均衡,计算复杂性

论文标题:An impossibility theorem in game dynamics论文来源:PNAS斑图链接:https://pattern.swarma.org/paper/97aefbf2-63e0-11ee-963a-0242ac17000d原文链接:https://www.pnas.org/doi/10.1073/pnas.2305349120
纳什均衡是博弈论中的主要解决方案概念,不仅在经济学领域起着核心作用,还在其他领域中扮演着重要角色。它表示玩家在游戏中做出的选择组合,其中没有自私的玩家会改变他们的决策。尽管每个游戏都有一个纳什均衡,但目前尚不清楚在重复进行游戏的玩家中是否存在确定性行为,可以保证从任何起始点都收敛到游戏的纳什均衡。如果假设玩家的行为是一个离散时间或连续时间规则,其中当前的混合策略配置映射到下一个策略配置,那么这个问题就变成了动力系统理论的问题。
作者应用这个理论,特别是Conley指标理论(Conley index theory),来证明 一个普遍的不可能性结果:存在一些游戏,所有的游戏动态都无法从任何起始点收敛到纳什均衡,帮助证明这个不可能性结果的游戏是退化的,但同时猜想,在计算复杂性的假设下,非退化游戏也会得出相同的结果。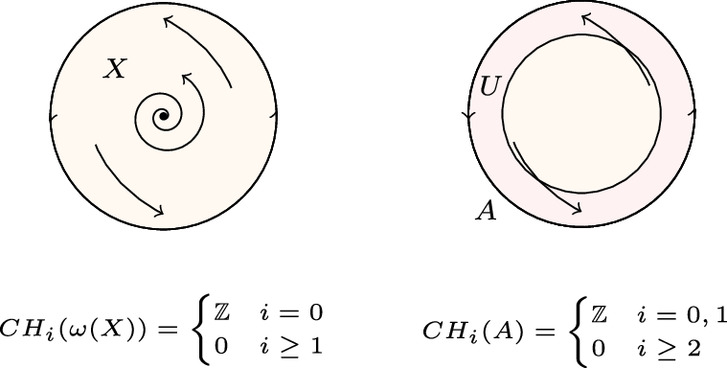 图1 一个半流的基本Conley指数计算
图1 一个半流的基本Conley指数计算
文章还对近似纳什均衡解概念证明了更强的不可能性结果:对于一组具有正测度的游戏,没有博弈动力学可以在考虑到足够小但相对重要的近似误差时收敛到近似纳什均衡解集。结果表明,尽管纳什均衡及其受计算方法启发的近似解概念在所有游戏中都是通用的,但它们从根本上不足以预测长期玩家行为。
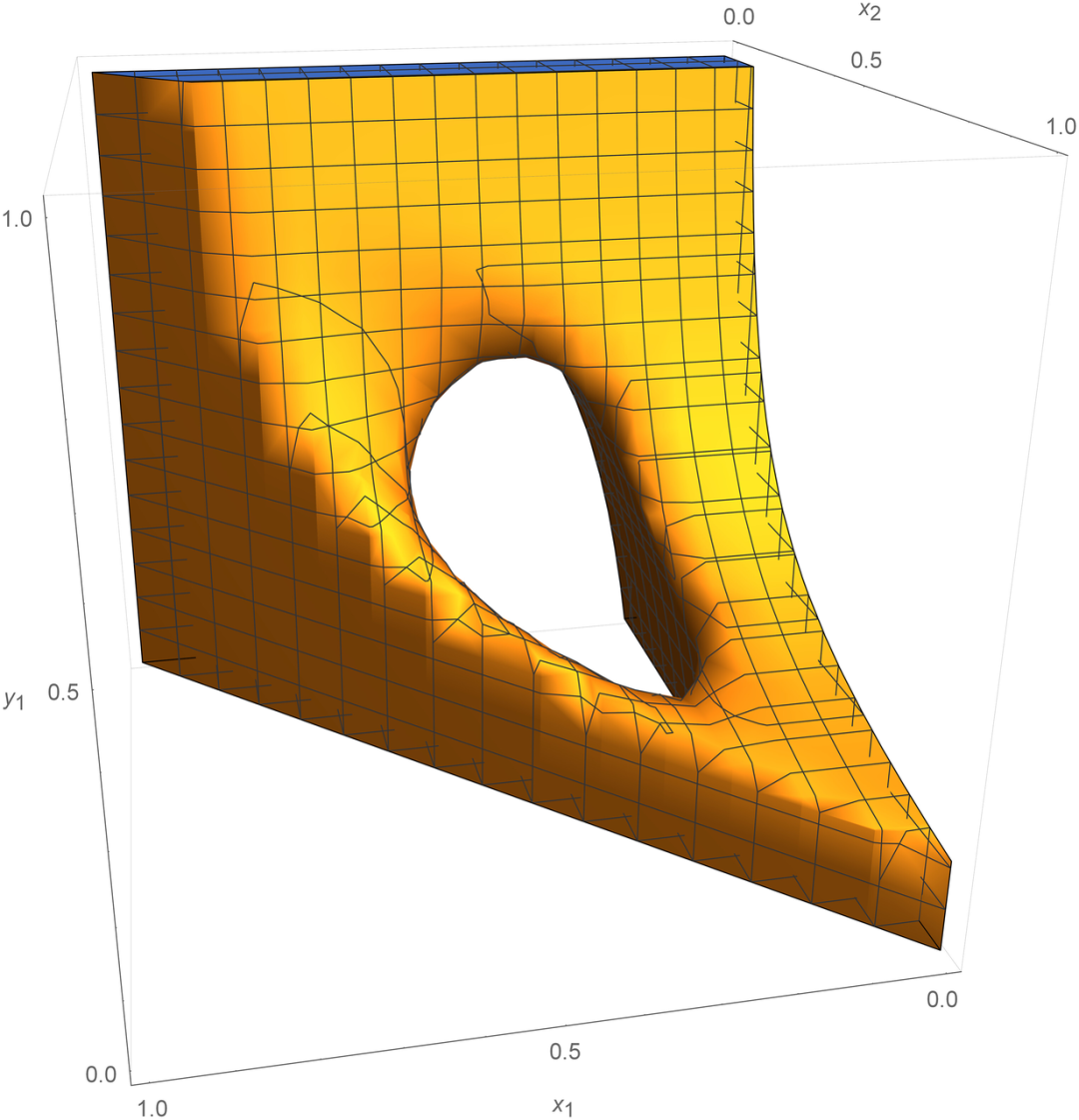
图2 游戏g的ϵ近似纳什均衡集的三维投影
编译|董佳欣
复杂科学最新论文
集智斑图顶刊论文速递栏目上线以来,持续收录来自Nature、Science等顶刊的最新论文,追踪复杂系统、网络科学、计算社会科学等领域的前沿进展。现在正式推出订阅功能,每周通过微信服务号「我的集智」推送论文信息。扫描下方二维码即可一键订阅:

推荐阅读
1. 囚徒困境:最经典的博弈论模型 | 集智百科2. 论文解读:辛梯度优化——多人博弈纳什均衡的全新解法3. 游戏博弈论:洞悉“剪刀-石头-布”背后的纳什均衡4. 张江:第三代人工智能技术基础——从可微分编程到因果推理 | 集智学园全新课程5. 成为集智VIP,解锁全站课程/读书会6. 加入集智,一起复杂!
点击“阅读原文”,追踪复杂科学顶刊论文




 ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง
ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง


