清华微软「LLM+推理智能体」超越GPT-4！攻克数理难题，斩获开源界MATH最佳成绩

  新智元报道  

编辑：润

【新智元导读】由清华大学和微软研究院共同的提出的TORA，结合了LLM的分布推理能力和外部程序的解决问题能力，将开源大模型的推理和数理能力推到了一个新的高度。

LLM不擅长数学的问题被彻底解决了？！

清华大学，微软研究院共同发表了一篇论文，创造性地提出了TORA：在LLM之外使用推理智能体，结合自然语言分布推理，就能大幅提高研究LLM的数理能力和推理能力。

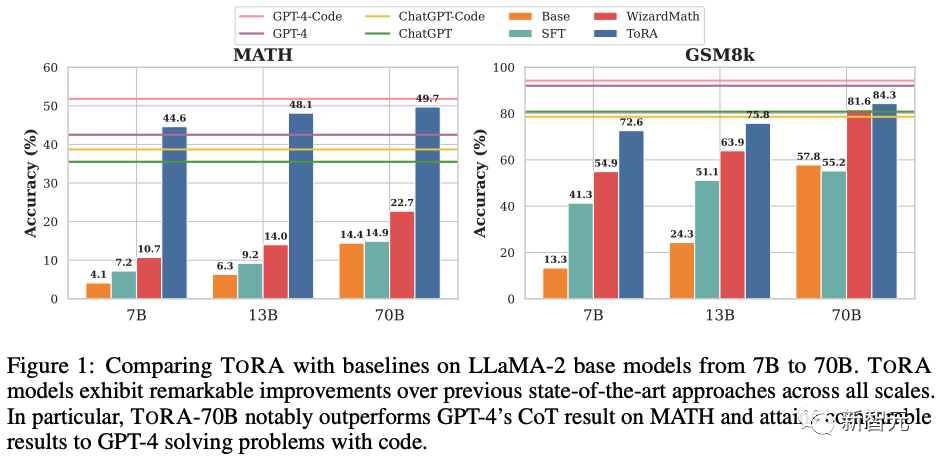
TORA在10个不同的数学推理数据集上实现了13%到19%的提升。TORA-7B模型，在非常具有挑战性的MATH数据集上得分为44.6%，远远超过最好的开源模型WizardMath-70B，提升高达22%！

论文地址：https://arxiv.org/abs/2309.17452

7B打70B，简直强无敌！

更加厉害的是，TORA-CODE-34B作为第一个在MATH数据集上准确率超过50%的开源模型，具有非常大的突破意义。

这一性能表现甚至超越了GPT-4的CoT成绩。

ToRA核心思路

目前，用LLM解决推理或者数理问题，最主要通过两个方法，一个是通过下图a中的自然语言分步骤推理的方法，第二个方法是通过结合外部的程序或者在模型之外执行程序的方法，来计算得出结果。

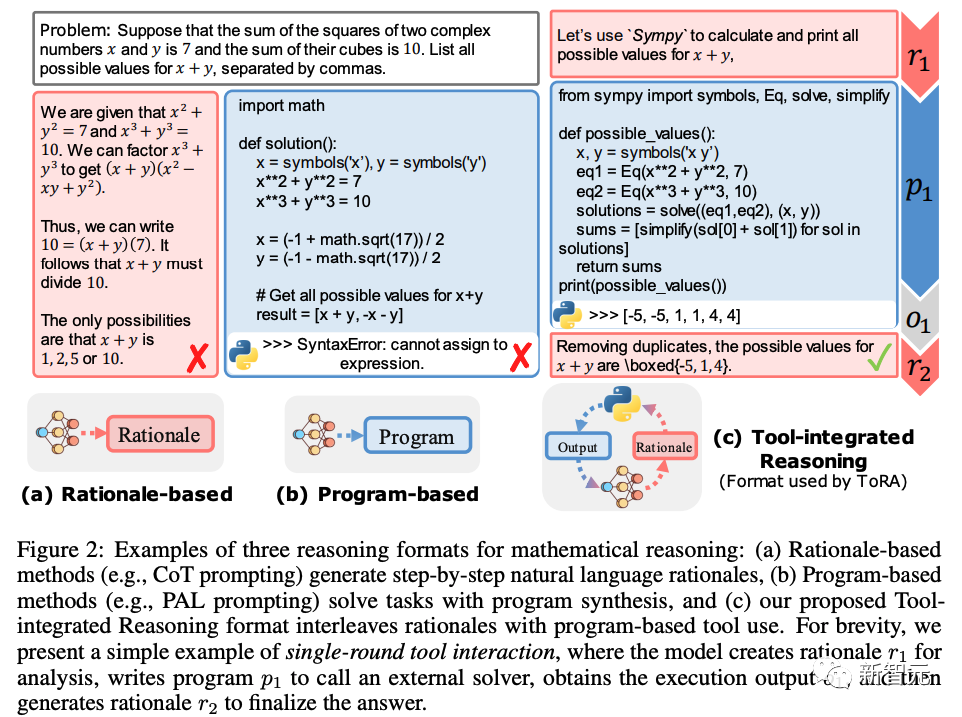
两种方法各有优势：

自然语言适用于语义分析、规划和抽象推理（例如常识推理），但在精确计算、符号操作和算法处理方面表现就较差。

相反，程序在严格的运算方面表现出色，并且可以将复杂的计算外包给方程求解器等专用工具大大提高计算准确结果。

为了充分利用自然语言推理和基于程序的工具使用的优势，研究人员基于LLaMA-2等开源模型进行训练，融合两个方法，用协同交叉的方式进行推理（如上图c所示)，从而大大缩小了与GPT-4等闭源模型在数学推理方面的差距。

研究人员首先设计了推理的交错格式（interleaving format），为来自GSM8k和MATH数据集的数学问题策划相应的交互式工具使用轨迹（interactive tool-use trajectories），然后在高质量注释（high-quality annotations）上应用模仿学习（imitation learning），从而取得比任何现有的开源模型更好的性能。

而且，由于选取的数据远远没有涵盖一个问题的所有有效轨迹，仅依赖模仿学习限制了模型的输出空间，阻碍了在测试过程中探索可能轨迹的灵活性。

为了增加合理推理步骤的多样性并减少不恰当的工具使用行为，研究人员应用输出空间塑形（output space shaping），还训练了模型在自我采样的有效轨迹，和经导师模型纠正过的无效轨迹（例如，34B模型可以作为7B模型的导师）上。

输出空间塑形显著提高了推理性能，使开源模型首次在竞赛级别的 MATH 数据集上达到超过50%的准确率。

研究人员评估了一系列从7B到70B的工具集成推理代理（TORA）在10个不同的数学推理数据集上的效果。如图1所示，TORA 系列在所有规模上都显著优于开源模型。

而且，在竞赛难度的MATH数据集上，TORA-7B的性能比之前的SoTA WizardMath-70B高出22%。TORA-CODE-34B 的结果比 GPT-4 的 CoT 结果高出8.3%（50.8% vs. 42.5%），并与GPT-4 Code（51.8%）相当。

TORA：用于数学推理的工具集成智能体

TORA系列通过利用自然语言推理和基于程序的工具使用来解决具有挑战性的数学问题。

如图2 (c) 所示，给定一个数学问题 q，TORA 会使用自然语言进行推理，产生 r1。

当到达更适合使用基于程序的工具进行后续任务的点时，例如方程求解，TORA 会根据自然语言指导 r1 生成一个用于工具使用的程序 p1。执行输出结果o1将被输送给TORA进行后续进一步的处理，包括工具使用调整、子任务求解或答案最终确定。

一直重复这个过程，直到模型将其答案放在「boxed{}」内。

所得轨迹表示为 ：

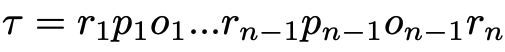
其中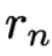包含答案。

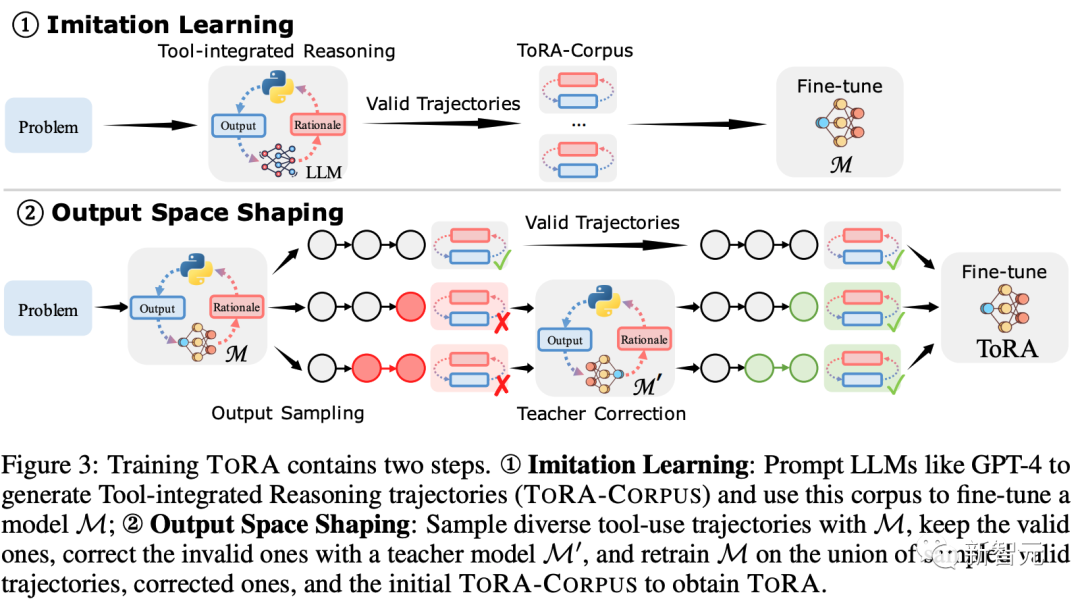
上图3展示了TORA的训练流程。

研究团队首先在流行的数学数据集上收集交互式工具使用轨迹。然后研究团队对结果注释应用模仿学习，并且输出空间塑造（space shaping）以进一步完善模型的推理行为。

收集交互式工具使用轨迹（INTERACTIVE TOOL-USE TRAJECTORIES）

现有的数学推理数据集主要包含自然语言或代码中的注释，由于缺少交互式工具使用注释，这为训练工具集成智能体带来了挑战。

为了解决这个问题，研究团队使用GPT-4在GSM8k和MATH训练集上合成高质量的轨迹。

研究团队选择GSM8k和MATH的原因，是因为它们展示了多样的推理模式，而且囊括了多个领域和难度级别的内容。

训练

模仿学习

研究人员在 TORA-CORPUS 上应用模仿学习，主要方式是最小化基于问题 q 的轨迹 τ 的负对数似然损失（ negative log-likelihood loss）：

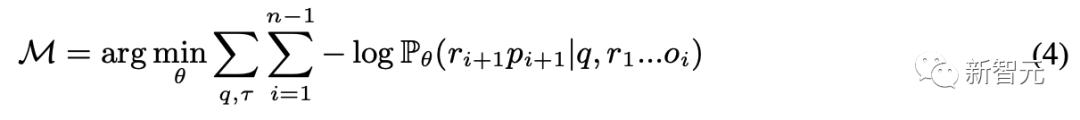
M是得到的模型。尽管 TORA-CORPUS 的规模较小，模仿学习还是获得了最先进的数学推理性能。

输出空间塑造（output space shaping）

对于每个问题，TORA-CORPUS大多只展示一个有效的交互式工具使用轨迹，这可能会限制模型的输出空间，使其在测试期间探索可能的轨迹时变得不够灵活。

因此，研究人员提出输出空间塑造，以鼓励合理推理步骤的多样性，并减少不当的工具使用行为。

为了探索多样的有效轨迹，研究人员对模仿学习模型M应用核采样（nucleus sampling），每个训练问题重复64次。

研究人员保留具有正确答案且没有工具使用错误的轨迹。

由于许多样本都是重复的，为了进一步提高多样性并试图纠正模型的不当行为，研究人员也寻求利用无效的轨迹。

研究人员观察到，答案错误的轨迹大多在中途就已经是错的，而之前的推理仍然是合理的；换句话说，研究人员可以通过纠正后续部分来获得有效的轨迹。

在研究人员的实验中，他们始终使用在TORA-CORPUS上训练的Code LLaMA-34B 作为教师模型，并对Code LLaMA系列（从7B到34B，带有模仿学习）应用采样。

研究人员共获得了233k个不同的有效轨迹样本和69k个纠正过的样本。

从这个组合数据集中，研究人员随机选择每个GSM8k和MATH问题最多4个轨迹，将它们与TORA-CORPUS合并，然后在得到的69k个注释上训练所有 TORA模型。

实验

实施细节

研究人员对 LLaMA-2和Code LLaMA系列（7B到70B）进行了微调，使用输出空间塑造的TORA-CORPUS，分别产生了TORA和TORA-CODE系列。

研究人员默认使用了2e-5的学习率，只有在34B和70B模型上使用了1e-5。

研究人员将全局批量大小设置为128，并使用了一个带有3%预热期的3个周期的线性调度器。

研究人员使用DeepSpeed ZeRO Stage3和Flash-Attention 2训练了所有模型。

研究人员对所有结果使用了贪婪解码，最大序列长度设置为2,048，工具执行的最大次数设置为3。

评估设置

数据集

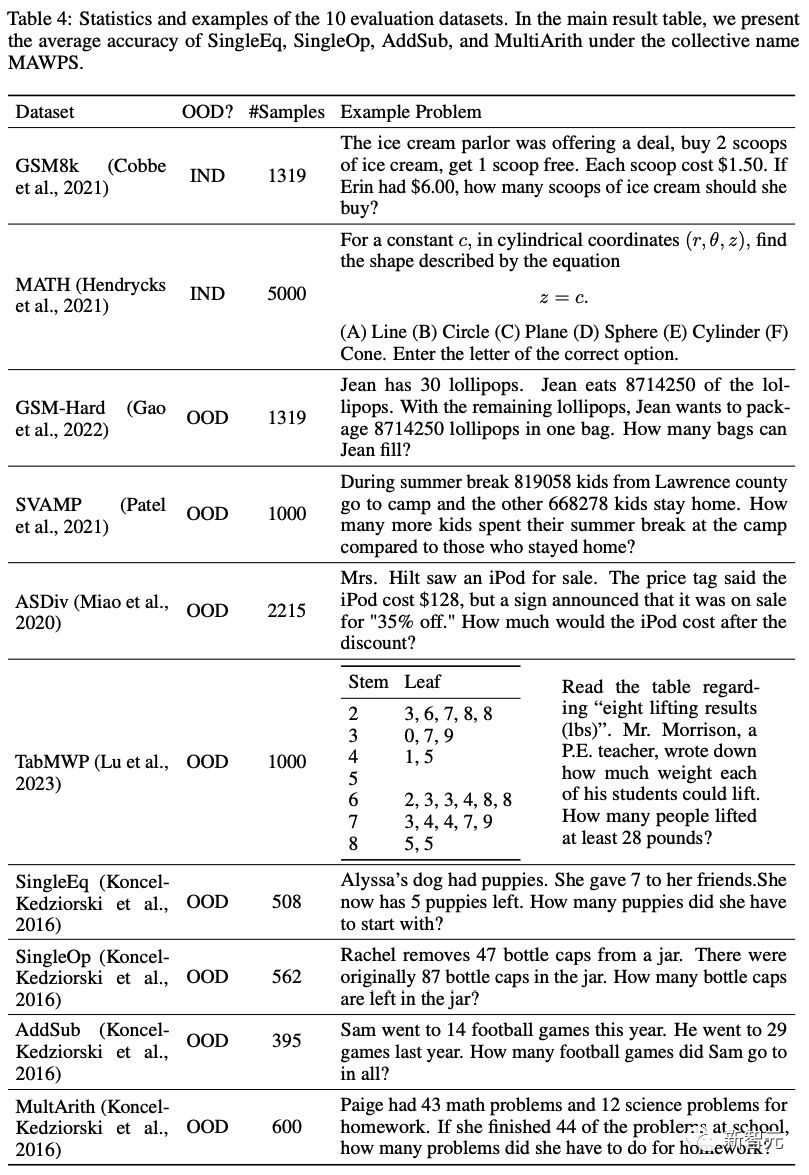
研究人员在GSM8k和MATH上评估了模型，还使用了8个分布外（out of distribution）的数据集，即GSM-Hard，SVAMP，ASDIV，TabMWP，SingleEQ，SingleOP，AddSub和MultiArith，如下表4所示。

这10个各种各样的数据集涵盖了从基础算术到竞赛级别的数学问题，覆盖了中学和高中的课程大纲以及各种数学领域。

问题格式也包括了基于表格的、自由格式的和多项选择题，确保对模型的数学推理能力进行了全面评估。

度量标准

研究团队展示了预测答案的准确率。

对于数值，研究团队进行四舍五入，而对于表达式，研究团队使用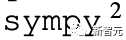进行解析。

由于SingleEQ, SingleOP, AddSub和MultiArith数据集专注于基础算术的不同方面，研究团队报告它们的平均结果，并为所有方法使用集合术语MAWPS。

基线

闭源模型

研究团队展现了一系列SoTA LLM的结果，如OpenAI的GPT-4、ChatGPT（gpt-3.5-turbo）、Google的PaLM-2和Anthropic的Claude-2。

默认情况下，研究团队呈现CoT提示结果，并为选定模型包括PAL提示结果。

开源模型

基础模型包括LLaMA-2和Code LLaMA，带有CoT和PAL提示。

有监督的微调（SFT）使用来自原始GSM8k和MATH数据集（15k样本）的CoT理由进行微调。

拒绝采样微调（RFT）利用多个模型生成多样的推理路径进行微调。WizardMath使用ChatGPT增强数据，并进行SFT和RLHF。

Platypus-2是抱抱脸LLM排行榜上的顶级模型，使用Open-Platypus推理数据集进行了微调。

研究团队还将TORA与Toolformer进行比较，后者是一个被训练用来使用计算器的模型。

主要结果

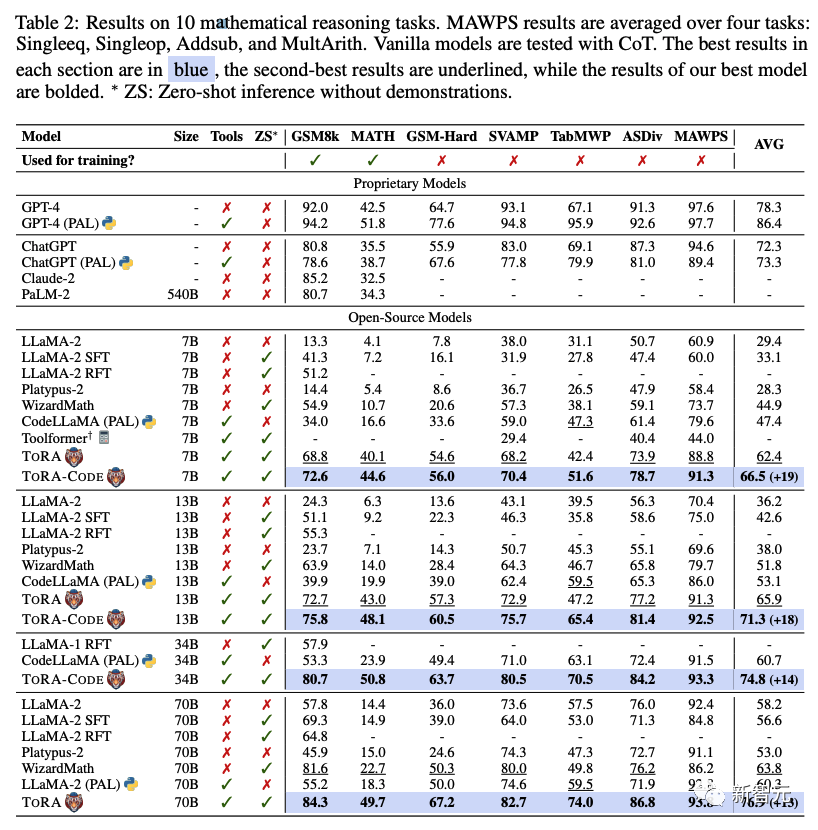
表2展示了TORA在10个数学数据集上的结果，主要结果是：

（1）使用交错格式和输出空间塑造，TORA在所有规模上始终超过先前最先进的开源模型，在10个任务中实现了13%到19%的绝对提高。

（2）TORA-70B在GSM8k（84.3% vs. 80.4%）和MATH（49.7% vs. 38.7%）上显著优于ChatGPT，无论是CoT还是PAL提示，而TORACODE-34B在使用代码解决竞赛级MATH数据集时与GPT-4旗鼓相当（50.8% vs. 51.8%）。

（3）TORA-CODE的准确率比同尺寸的TORA高约5%，证明在代码数据上继续训练显著有助于基于程序的工具使用。

（4）虽然基于推理的微调对分布外泛化产生了负面影响，但TORA显示出优越的泛化能力。例如，WizardMath-70B在TabMWP上的表现不如基模型（49.8% vs. 57.5%），而TORA-70B有效地泛化到这种表格推理任务（74.0%）。

（5）TORA实现了快速的领样本推理速度，在每个问题上平均1.02个工具交互轮次，同时有效地处理需要交互工具使用的问题。

参考资料：https://arxiv.org/abs/2309.17452v2