新信息论：从分解到整合｜因果涌现读书会第四季启动

750次阅读

没有评论

研读硬核论文，分享学界前沿成果，激发科研合作灵感，聚焦“新信息论”度量指标，探讨意识如何涌现…… 因果涌现系列读书会第四季来了！
研究领域：信息论，整合信息论，信息分解，整合信息分解，因果涌现，意识理论

读书会背景

什么是意识？意识能否度量？机器能否产生意识？对于意识问题，人们可能即将迎来一个大的突破，各种有关意识的理论正如雨后春笋般展现出勃勃生机。在诸多理论中，神经科学家 Giulio Tononi 的整合信息论（Integrated Information Theory，简称IID）被认为是最有前景的意识理论之一。该理论的核心是提出了一个度量意识程度的指标 Φ，而这个指标恰恰是基于 Shannon 提出的互信息（Mutual Information），因此你也可以把整合信息论理解为信息论的一种延展。
另外，如果你相信意识是大脑神经活动的一种涌现结果，那么什么是涌现便成为了理解意识过程中一个重要环节。事实上，Erik Hoel 和 Giulio Tononi 共同提出的因果涌现理论恰恰是对基于Φ的意识理论的一个扩展。因果涌现理论目前发展出两个派别，除了Erik Hoel的有效信息因果涌现框架以外，还有一个是 Rosas 的信息分解（Partial Information Decomposition，简称PID）框架。而PID恰恰是对 Shannon 的互信息（Mutual Information）进行进一步地拆分，用协同（Synergy）、冗余（Redundency）和特有（Unique）这三种度量尝试刻画多变量系统的复杂关系。更进一步，Rosas基于信息分解理论又提出了融合了整合信息论的信息分解框架ΦID，并基于此尝试构建新的意识理论。
一边是信息整合（IIT），一边是信息分解（PID），这看起来很分裂，但其实它们的背后都是互信息（I），这是当年 Shannon 用于理解通信的一般理论，刻画信道容量而提出的一种度量指标。从这个意义上来说，IIT 和 PID 都是对 Shannon 信息论的进一步发展。我们这一期的读书会也恰恰就聚焦在这些“新信息论”度量指标上。对这些指标的理解，不仅有利于我们理解什么是意识，什么是涌现，更能够拓宽我们的视野，找到不同学科，不同问题背后的统一性原理。
为了更好地理解这些信息框架与测度，并将这些前沿技术应用于交叉领域的研究工作中，本次读书会将梳理信息论领域的发展脉络，从信息熵的概念开始，逐步梳理各种信息测度的意义及其间的联系。其中我们将重点关注整合信息论以及信息分解这两个前沿话题，并展开相关应用研究的研读与分享活动。我们希望借此读书会理解并跟踪信息测度领域的前沿进展，对什么是信息，以及信息论领域的前沿工具在涌现、意识、自由意志中的作用、功能、如何应用，有更深入的思考，并交流探索信息测度与复杂系统交叉领域的研究内容。

参加完本次读书会，你将收获：

对“新信息论”以及它是如何从信息论中发展而来的完整脉络；
了解涌现的定量理论；
了解意识的定量理论：整合信息论；
理解信息整合与信息分解的本质，为跨学科应用做好准备。

读书会框架

此次读书会将首先对信息论领域进行整体回顾，介绍经典信息指标，希望建立对信息熵的直觉，给后面的内容打基础。第二部分介绍整合信息论的理论框架。第三部分将详细梳理信息分解的理论框架，包括部分信息分解（PID）、延展的PID框架、信息分解计算，以及信息论在脑与复杂系统中的应用。最后介绍整合信息分解（ΦID）与 Rosas 的因果涌现框架。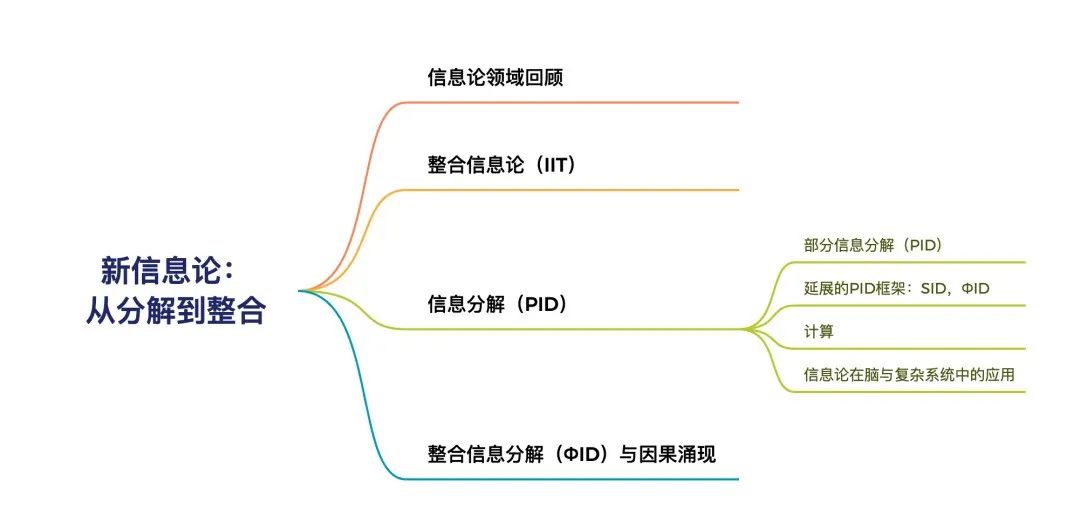

读书会发起人

张江，北京师范大学系统科学学院教授，集智俱乐部、集智学园、集智科学研究中心创始人，曾任腾讯研究院、华为战略研究院等特聘顾问。主要研究领域包括复杂系统分析与建模、规模理论等。集智斑图个人主页：https://pattern.swarma.org/user/9

袁冰，集智科学研究中心技术与产品顾问。毕业于华中科技大学，研究兴趣包括因果推断、复杂科学，以及人工智能相关领域。曾于西门子，甲骨文，唯品会等公司研发部门任职。集智斑图个人主页：https://pattern.swarma.org/user/46173
吕奥博，圣路易斯华盛顿大学（WUSTL）系统科学与数学系研究生，研究方向为系统科学、信息论等。集智斑图个人主页：https://pattern.swarma.org/user/74882

第一期讲者招募

读书会第一期，我们希望和大家共读共研一篇最新发表的综述文章：《大脑层次结构中是否可以涌现出通过向下因果来控制神经活动的协同核心？》。感兴趣的朋友认领其中的部分段落，解析重点概念，欢迎大家报名参与！（详情请咨询读书会运营负责人）论文题目：Can there be a synergistic core emerging in the brain hierarchy to control neural activity by downward causation?论文链接：https://www.authorea.com/users/655476/articles/661267-can-there-be-a-synergistic-core-emerging-in-the-brain-hierarchy-to-control-neural-activity-by-downward-causation因果涌现社区对文章的完整翻译：科学能解释自由意志吗？

我们欢迎从事相关问题研究的老师、同学报名参与交流，不限专业背景，特别欢迎有交叉学科背景的朋友参加。读书会的分享交流以论文、专著为基础，需要一定的背景知识与论文阅读能力。如果你缺少研究基础但兴趣特别浓厚，也欢迎报名。

报名参加读书会

本读书会谢绝参与的对象为确保专业性和讨论的聚焦，本读书会谢绝脱离读书会文本和复杂科学问题本身的空泛的哲学和思辨式讨论；不提倡过度引申在社会、人文、管理、政治、经济等应用层面的讨论。我们将对参与人员进行筛选，如果出现讨论内容不符合要求、经提醒无效者，会被移除群聊并对未参与部分退费，解释权归集智俱乐部所有。
运行模式本季读书会预计讨论分享8～10次，按暂定框架贯次展开；每周进行线上会议，由 1-2 名读书会成员以PPT讲解的形式领读相关论文，与会者可以广泛参与讨论，会后可以获得视频回放持续学习。
举办时间2023年11月19日开始，每周日上午 9:00-11:00，持续时间预计 8～10 周。我们会对每次分享的内容进行录制，剪辑后发布在集智斑图网站上，供读书会成员回看，报名的成员可以根据情况自由安排学习时间。
参与方式此次读书会为线上闭门读书会，采用的会议软件是腾讯会议（请提前下载安装）。在扫码完成报名并添加负责人微信后，负责人会将您拉入交流社区（微信群），入群后告知具体的会议号码。
报名方式第一步：扫码填写报名信息扫码报名读书会网页地址：https://pattern.swarma.org/study_group/35

第二步：填写信息后，付费299元。

第三步：添加负责人微信，拉入对应主题的读书会社区（微信群）。

本读书会可开发票，请联系相关负责人沟通详情。
针对学生的退费机制读书会通过共学共研的机制，围绕前沿主题进行内容梳理和沉淀，所以针对于学生，可以通过参与共创任务，获取积分，积分达到退费标准之后，可以直接退费。

加入社区后可以获得的资源

在线会议室沉浸式讨论：与主讲人即时讨论交流

交互式播放器高效回看：快速定位主讲人提到的术语、论文、大纲、讨论等重要时间点

高质量的主题微信社群：硕博比例超过80%的成员微信社区，闭门夜谈和交流

超多学习资源随手可得：从不同尺度记录主题下的路径、词条、前沿解读、算法、学者等

参与社区内容共创任务：读书会笔记、百科词条、公众号文章、论文解读分享等不同难度共创任务，在学习中贡献，在付出中收获。

共享追踪主题前沿进展：在群内和公众号分享最新进展，领域论文速递

参与共创任务，共建学术社区

读书会笔记：在交互式播放器上记录术语和参考文献

集智百科词条：围绕读书会主题中重要且前沿的知识概念梳理成词条。例如：

论文解读分享：认领待读列表中的论文，以主题报告的形式在社区分享

公众号文章：以翻译整理或者原创生产形式生产公众号文章，以介绍前沿进展。例如：

论文翻译

科普文章翻译

讲座整理

PS：具体参与方式可以加入读书会后查看对应的共创任务列表，领取任务，与运营负责人沟通详情，上述规则的最终解释权归集智俱乐部所有。

论文阅读清单

1. 信息论领域回顾（经典信息指标）

为了深入理解信息论前沿测度与框架，有必要梳理信息论领域的发展脉络，建立对于信息熵以及信息相关测度的理解。

Shannon, C. E. (1948). A mathematical theory of communication. The Bell system technical journal, 27(3), 379-423.

本文是信息论领域的起点。本次读书会涉及到的信息分解是在香农公式的基础上对三变量以上的变量上进行进一步的分解，因此理解经典的两变量韦恩图十分必要。深刻理解条件熵、互信息这些指标的意义对于理解信息分解框架十分必要。

Bell, A. J. (2003, April). The co-information lattice. In Proceedings of the fifth international workshop on independent component analysis and blind signal separation: ICA (Vol. 2003).

多变量的互信息（冗余信息）以及信息晶格的概念在信息论领域很早就已经存在，理解信息论领域的发展脉络有助于理解PID以及信息分解在当前信息论领域的发展进程。

Te Sun, H. (1978). Nonnegative entropy measures of multivariate symmetric correlations. Information and Control, 36, 133-156.

本文系统梳理了熵在动力系统中的发展和应用的历史视角。

Katok, A. (2023). Fifty years of entropy in dynamics: 1958–2007. In Frontiers in Entropy Across the Disciplines: Panorama of Entropy: Theory, Computation, and Applications (pp. 353-404).

提供了熵在动力系统中的发展和应用的历史视角。

Cover, T. M. (1999). Elements of information theory. John Wiley & Sons.信息论的综述书籍，涵盖了各种与熵相关的度量。

相关文献

Lizier, J. T., Heinzle, J., Horstmann, A., Haynes, J. D., & Prokopenko, M. (2011). Multivariate information-theoretic measures reveal directed information structure and task relevant changes in fMRI connectivity. Journal of computational neuroscience, 30, 85-107.

利用互信息与传递熵探讨脑中的多变量间结构，文中不涉及PID，但是可以作为读书会中探讨PID框架相较于现有信息测度的进步。

2. 整合信息论

Tononi Giulio, Boly Melanie, Massimini Marcello, et al. Integrated Information Theory: From Consciousness to Its Physical Substrate. Nature Reviews Neuroscience, 2016, 17(7): 450–461整合信息论（IIT）的全面性综述文章。
Oizumi, M., Albantakis, L., & Tononi, G. (2014). From the phenomenology to the mechanisms of consciousness: integrated information theory 3.0. PLoS computational biology, 10(5), e1003588.整合信息论 3.0版本的介绍。

相关文献

Chang AY, Biehl M, Yu Y, Kanai R. Information Closure Theory of Consciousness. arXiv preprint arXiv:190913045. 2019

一种新的意识理论
Giulio Tononi and Olaf Sporns: Measuring information integration, BMC Neuroscience 2003, 4:31

可能是IIT最早的版本
Measuring Integrated Information: Comparison of Candidate Measures in Theory and Simulation, https://www.mdpi.com/1099-4300/21/1/17/htm
Sara Imari Walker, Hyunju Kim and Paul C. W. Davies,The informational architecture of the cell, Phil. Trans. R. Soc. A 374: 20150057.

把IIT应用到细胞的一种尝试，IIT的跨学科应用。
Krzysztof Chalupka, Pietro Perona, Frederick Eberhardt: Multi-Level Cause-Effect Systems, Proceedings of the 19th International Conference on Artificial Intelligence and Statistics (AISTATS) 2016
Survey of Consciousness Theory from Computational Perspective At the Dawn of Artificial General Intelligence. https://browse.arxiv.org/pdf/2309.10063.pdf
Yurchenko, Sergey B. “Is information the other face of causation in biological systems?.” Biosystems 229 (2023): 104925. https://www.sciencedirect.com/science/article/abs/pii/S0303264723001004

3. 信息分解
信息分解是一个希望更细粒度分解信息熵的概念模型（Measure），这个模型目前由几个公理组成。在这个概念模型中，更细粒度的信息原子在不同场景下能够代表不同的物理意义，从而实现了更加精细的测度。然而尽管目前很多人提出了尽可能满足这个公理的计算方法，但是这些计算方法在现实问题的应用中仍存在一些问题，这些问题限制了信息分解在很多问题中的应用。这次读书会的重点将会是Rosas提出的利用ΦID度量因果涌现的概念模型，以及其他PID相关应用。

3.1 部分信息分解（PID）

Williams, P. L., & Beer, R. D. (2010). Nonnegative decomposition of multivariate information. arXiv preprint arXiv:1004.2515.

提出信息分解的文章，介绍了部分信息分解PID框架，并提出了第一个（数值类）计算方法，也是目前最经典的方法。

论文解读：《互信息的“微积分”》

A Lyu, B Yuan, O Deng, M Yang, A Clark, J Zhang. System Information Decomposition. arXiv preprint arXiv:2306.08288 (2023).

提出系统信息分解SID，这是一个在PID框架基础之上拓展框架，能够以一个全局的视角来观察多远变量的各种信息熵指标。

Rassouli, B., Rosas, F. E., & Gündüz, D. (2019). Data disclosure under perfect sample privacy. IEEE Transactions on Information Forensics and Security, 15, 2012-2025.

协同披露，用到了部分信息分解理论框架中的协同现象，不涉及计算问题。

相关资料：因果涌现读书会第二季分享

张章：信息分解方法及其在复杂系统中的应用https://pattern.swarma.org/study_group_issue/227
刘凯威：保护数据隐私下的信息披露https://pattern.swarma.org/study_group_issue/304
张章：协同披露的信息分解https://pattern.swarma.org/study_group_issue/229

3.2 信息分解计算

Kolchinsky, A. (2022). A novel approach to the partial information decomposition. Entropy, 24(3), 403.

一种借助信息熵性质（偏序关系）的优化类PID计算方法。文章也回顾了很多其他计算方法。

Finn, C., & Lizier, J. T. (2018). Pointwise partial information decompositionusing the specificity and ambiguity lattices. Entropy, 20(4), 297.

一种利用事件熵（Pointwise entropy 逐点熵）的数值类PID计算方法。相较于Beer的计算方法更加具有可解释性。文章回顾了信息熵与事件熵的发展，比较适合一开始介绍。

相关文献

Bertschinger, N., Rauh, J., Olbrich, E., Jost, J., & Ay, N. (2014). Quantifying unique information. Entropy, 16(4), 2161-2183.

一种利用信息原子约束进行的优化类（三变量）PID计算方法。是一个有趣的对信息分解定量方法的探索思路。
Harder, M., Salge, C., & Polani, D. (2013). Bivariate measure of redundant information. Physical Review E, 87(1), 012130.
Banerjee, P. K., Rauh, J., & Montúfar, G. (2018, June). Computing the unique information. In 2018 IEEE International Symposium on Information Theory (ISIT) (pp. 141-145). IEEE.

优化类PID定量方法，对于算法的收敛性及效率有讨论，属于优化类算法中较为成熟的。
Ince, R. A. (2017). Measuring multivariate redundant information with pointwise common change in surprisal. Entropy, 19(7), 318.
Finn, C., & Lizier, J. T. (2018). Pointwise partial information decompositionusing the specificity and ambiguity lattices. Entropy, 20(4), 297.
Olbrich, E., Bertschinger, N., & Rauh, J. (2015). Information decomposition and synergy. Entropy, 17(5), 3501-3517.
Niu, X., & Quinn, C. J. (2019, July). A measure of synergy, redundancy, and unique information using information geometry. In 2019 IEEE International Symposium on Information Theory (ISIT) (pp. 3127-3131). IEEE.
Bertschinger, N., Rauh, J., Olbrich, E., & Jost, J. (2013). Shared information—New insights and problems in decomposing information in complex systems. In Proceedings of the European conference on complex systems 2012 (pp. 251-269). Springer International Publishing.

相关资料：因果涌现读书会第二季分享

吕奥博：关于信息分解框架的讨论https://pattern.swarma.org/study_group_issue/249https://pattern.swarma.org/study_group_issue/255

3.3 PID 作为测度的应用

Varley, T. F. (2023). Uncovering Higher-Order Structures in Complex Systems with Multivariate Information Theory (Doctoral dissertation, Indiana University).PID 在脑网络中的应用
相关文献Wibral, Michael, et al. Partial information decomposition as a unified approach to the specification of neural goal functions. Brain and cognition 112 (2017): 25-38. https://www.sciencedirect.com/science/article/pii/S027826261530021X

4. 整合信息分解（ΦID）与因果涌现

整合信息分解框架能够将PID扩展到了马尔科夫系统，从而可以将静态的PID用于衡量具有时间属性的因果涌现。

Mediano, P. A., Rosas, F., Carhart-Harris, R. L., Seth, A. K., & Barrett, A. B. (2019). Beyond integrated information: A taxonomy of information dynamics phenomena. arXiv preprint arXiv:1909.02297.

提出整合信息分解（ΦID）的理论文章，将整合信息的指标Φ与信息分解框架相结合。该框架在下一篇文章中将被用来定义因果涌现。

Andrea I Luppi, Pedro A M Mediano, Fernando E Rosas, David J Harrison, Robin L Carhart-Harris, Daniel Bor, Emmanuel A Stamatakis, What it is like to be a bit: an integrated information decomposition account of emergent mental phenomena, Neuroscience of Consciousness, Volume 2021, Issue 2, 2021, niab027, https://doi.org/10.1093/nc/niab027

Rosas, F. E., Mediano, P. A., Jensen, H. J., Seth, A. K., Barrett, A. B., Carhart-Harris, R. L., & Bor, D. (2020). Reconciling emergences: An information-theoretic approach to identify causal emergence in multivariate data. PLoS computational biology, 16(12), e1008289.

本文提出了基于整合信息分解的因果涌现定义，利用了一组充分指标规避了信息分解无法精确计算的问题，并在三个例子中进行了验证。

论文翻译：《量化涌现：信息论方法识别多变量数据中的因果涌现》
相关资料：

吕奥博、邓鸥：信息论方法识别多元数据中的因果涌现https://pattern.swarma.org/study_group_issue/239

扫码阅读并收藏读书会参考文献列表斑图路径：https://pattern.swarma.org/article/261

因果涌现社区

跨尺度、跨层次的涌现是复杂系统研究的关键问题，生命起源和意识起源这两座仰之弥高的大山是其代表。因果涌现理论、机器学习重整化技术、信息论或信息分解等近年来新兴的理论与工具，有望破解复杂系统的涌现规律。
集智俱乐部因果涌现读书会目前已经进行了三季。第一季读书会系统地梳理了因果涌现的概念，以及它与Sloopy Model、复杂性阈值、自指等概念之间的联系，也探讨了因果涌现理论在复杂网络、机器学习中的应用。参看：因果涌现读书会启动：连接因果、涌现与自指——跨尺度动力学与因果规律的探索。
第二季读书会探讨了涌现、因果科学和机器学习三大主题的融合，包括信息论拓展、因果涌现理论、因果表示学习、多尺度机器学习动力学建模。请参看：因果、涌现与机器学习：因果涌现读书会第二季启动。
第三季读书会进一步围绕因果涌现的核心问题「因果涌现的定义」以及「因果涌现的辨识」进行深入学习和讨论，对 Erik Hoel 提出的 Causal Emergence，Causal Geometry 等因果涌现的核心理论进行探讨和剖析，并详细梳理其中涉及到的方法论，包括从动力学约简、隐空间动力学学习等其他领域中学习和借鉴相关的研究思路，最后探讨因果涌现的应用，包括基于生物网络、脑网络或者涌现探测等问题展开扩展，发掘更多的实际应用场景。请参看：因果涌现读书会第三季启动：深入多尺度复杂系统核心，探索因果涌现理论应用
此次读书会主题是「新信息论：从分解到整合」，是因果涌现系列读书会的第四季，将重点梳理信息分解与整合信息论的相关研究。
因果涌现社区聚集了600+成员，积累了大量论文解读资料。欢迎感兴趣的朋友报名，加入因果涌现社区，解锁对应录播权限。

因果涌现读书会回放视频

第一季：https://pattern.swarma.org/study_group/7

第二季：https://pattern.swarma.org/study_group/16

第三季：https://pattern.swarma.org/study_group/28因果涌现社区共创的文章

集智俱乐部读书会

集智俱乐部读书会是面向广大科研工作者的系列论文研读活动，其目的是共同深入学习探讨某个科学议题，了解前沿进展，激发科研灵感，促进科研合作，降低科研门槛。读书会活动始于 2008 年，至今已经有 40 余个主题，内容涵盖复杂系统，人工智能，脑与意识，量子纠缠，张量网络，计算社会科学等。凝聚了众多优秀科研工作者，促进了科研合作发表论文，孵化了许多科研产品。如 2013 年的“深度学习”读书会孕育了彩云天气 APP，2015 年的“集体注意力流”读书会产生了众包书籍《走近2050》等。集智俱乐部从2020年开始举办线上读书会，目前已有因果科学、生命复杂性、图神经网络、复杂系统自动建模、因果涌现、复杂经济学、计算社会科学、后ChatGPT、AI+Science 等主题的读书会，沉淀了丰富的主题和讨论，请参看读书会合集。欢迎感兴趣的朋友在集智斑图网站（pattern.swarma.org）深入探索。
点击“阅读原文”，报名读书会