在之前 RTMPose 的社区开放麦里,我有浅浅分析一下 SimCC 定位范式与 Heatmap 定位范式的不同,但因为时间和篇幅都有限,当时只能略微提一下。眼下随着工作重心逐渐转向 LLM,以后亲力亲为搞 Pose 相关算法的机会可能会渐渐变少了,因此还是打算写一篇笔记来记录一下,也许可以对大家有所启发。这些内容暂时只是我个人的一些猜想,没有经过严谨的数学论证,因此欢迎大家讨论或者指正。
开放麦录像在 B 站和 OpenMMLab 公众号,以及我个人公众号都能搜到,这一段的分析在视频的41分钟到45分钟部分。
链接如下:https://www.bilibili.com/video/BV1Wc411p7HT
总体而言就是这页 PPT :
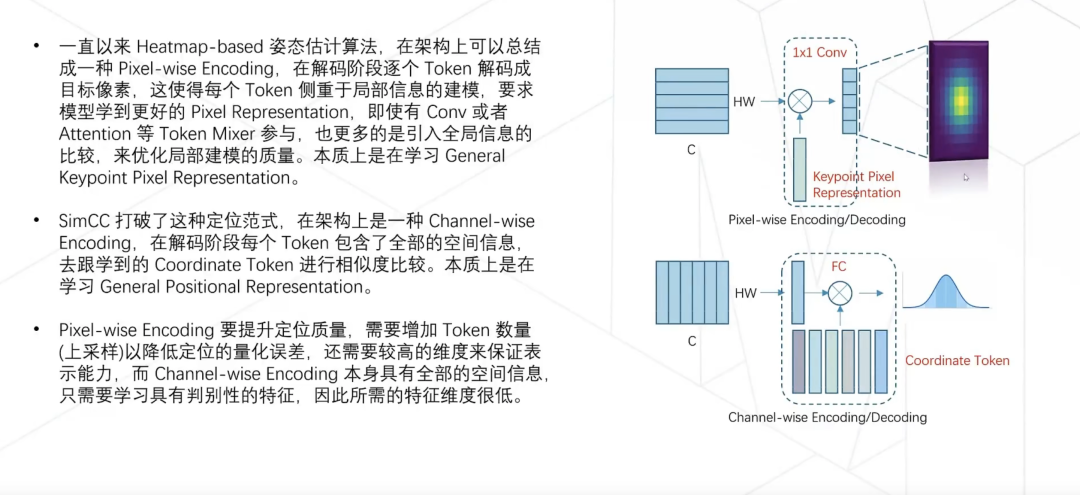
首先让我们回顾一下 Heatmap 算法的计算方式:
- 图片经过 Backbone 提取到的特征经过转置卷积提升分辨率后,得到一个特征图 (C, H, W)
- 特征图经过一层 1×1 卷积得到 (K, H, W) 的 Heatmap,其中 K 等于关键点个数
- 对于每一个关键点的预测,我们使用一张二维的高斯分布来监督,逐点计算 MSE loss
回顾卷积层的运算我们会知道,1×1 卷积等价于全连接层,即,Conv2d(C, K, kernel_size=1) 等价于 Linear(C, K),而这个全连接层的本质则是下面这个矩阵运算:
简单起见我们可以把 bias 去掉,再进一步简化问题,考虑 K = 1的情况,因此最后这一层矩阵运算,本质上是在让 HW 空间上的每一条向量与卷积层里的一维权重向量求内积,因此实际计算了 HxW 次 矩阵运算,也就是这张图表示的过程和结果:
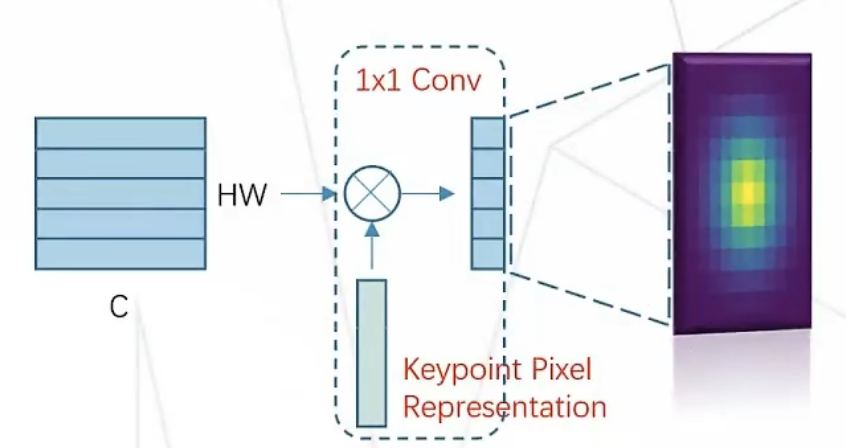
因为内积操作可以看成是比较两个向量相似度的过程(假如两个向量都被归一化,内积运算等于求余弦相似度),所以自然而然地,得到了一张 Heatmap ,且具有如下性质:
- 响应值最大的点也就是向量相似度最大的像素
- 响应值最大点附近的点相似度也会高,呈现出随着距离衰减的特点
让我们来尝试分析一下这个过程:
- 直观地,输入图片空间上每块区域的特征,被 Backbone 压缩成了一条一条 C 维向量,用时髦一点的说法讲成 token 或者 embedding 也可
- 在训练过程中,卷积层里的那条一维向量会被更新,因为模型全靠这条向量跟图片 token 的相似度来定位关键点,因此这条向量我们可以认为是学到了这个关键点相关的局部特征或者说,知识
- 所以整个 Heatmap 方法训练的过程,本质上是在学习一个“任何条件(光照、背景、风格 etc.)下的这个关键点的通用表示或压缩结果”
SimCC 方法简言之,把每个关键点的 x 和 y 坐标拆开单独定位,因此不再需要维护二维的特征图,而是各自进行一维的定位。定位过程可以看成是在做分类,把每个像素看成一类,分类的预测结果也就是对应的像素坐标。
坐标分类的思想在如今想来,我感觉更像是讲故事耍的一个小花招,既是巧妙之处,也是很多人一开始不好理解的地方。本质上讲,与其说 SimCC 是把定位过程看成分类问题,不如说是把一维坐标定位看成离散的一维分布的预测问题,分类问题目前的做法(Softmax + CrossEntropy)本质上也是在让网络预测一维离散分布。
SimCC 的计算方式为:
- 图片经过 Backbone 提取得到一个特征图 (C, H, W)
- 特征图经过一层 1×1 卷积得到 (K, H, W) 的特征图,其中 K 等于关键点个数
- 把特征图的最后两维合并,也就是把二维特征拉直成一维,得到 (K, HW) 的矩阵,也就是 K 个长度为 HW 的一维向量
- 每一个关键点对应的向量,去跟我们预先准备好的 N 个权重向量求内积,得到一维上的“Heatmap”,我们使用一维高斯分布来监督,计算 KL 散度作为损失
以上过程对应的是这张图(图中的 C 对应上述过程的 K):
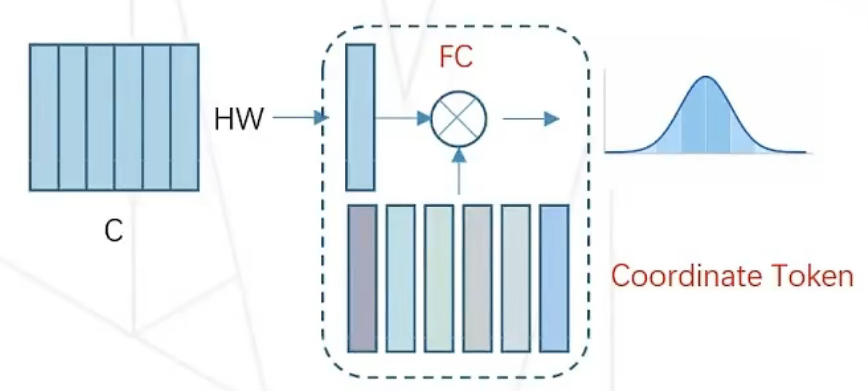
SimCC 方法与 Heatmap 相似之处主要在于:
- 都有用到高斯分布来进行监督
- 最后的定位层都是全连接层,也就是向量的内积运算
但他们本质上的含义在我看来却是差别很大的:
- 可学习的权重变了,SimCC 可学习的部分是 N 个权重向量(位置向量),而不是一个关键点向量
- 可学习权重的含义也发生了变化,每个权重向量代表的是连续空间上的一个个均匀排列的离散采样点位置
- SimCC 简单地把每个像素拆分成两个,并认为这些点是均匀排列的,但实际上这个均匀排列的性质是高斯分布这个对称的监督信息赋予的,对于一些特殊的数据分布,也许不均匀的坐标轴采样点排列会有奇效
- 在训练过程中,FC 层里的 N 个位置向量会被更新,模型通过预测的关键点向量跟这 N 个位置向量算内积来定位,因此我们可以认为预测的那个关键点向量里包含了位置信息
- 换言之,这 N 个位置向量可以看成是一种可学习的位置编码,模型是在学习一套位置编码的加密压缩方式,把整张图里的关键点信息压缩成 K 个对应的位置编码,然后用同一套码表(位置向量)就能解码出每个点的位置坐标
发现没有?SimCC 的过程里网络学习的核心不再是“关键点的通用表示”了。
不可否认,把图片压缩成位置编码的这个过程中,一定隐含着关键点信息的学习,但整个推理过程更接近于“图片->姿态->位置编码”,即把一张图片压缩某个学到的位置编码空间里的 K 个位置编码;而在 Heatmap 方法里,推理过程接近于“图片->姿态->关键点编码”,即把图片里的每个 patch 压缩成学到的关键点编码空间里的一个编码。
那么这样的定位范式有什么好处呢?
- 首先从学习难度上,位置编码比关键点编码所包含的信息要少太多了,因此信息压缩的难度要小很多,毕竟,你要区分两个位置向量,只需要相邻的向量相似度大一些,距离远的向量之间相似度小一些即可,具备这个性质的位置编码太容易学出来了
- 这样带来的好处是编码信息所需要的 bit 数大大降低,这也是 RTMPose 敢于把 SimCC 方法里的转置卷积层扔掉的原因,模型需要传递的信息变简单了,因此模型就可以做得更轻量
- 关键点编码的压缩则不然,不同关键点之间的相似度并不均匀,比如左右手的相似度当然是大于手和脸的,这些都意味着关键点编码需要的 bit 数是很大的,所以这个任务很难,模型参数量对于这个任务很关键
- 所以当模型参数量大到一定程度,ViTPose 用 Heatmap 方法的效果非常好,因为此时模型真正有能力去压缩出高质量的关键点编码了,而这个通用的关键点特征向量能用的地方和玩法就很多了,远远不是 SimCC 里的位置编码能相比的
再进一步,让我们用 Transformer 里 QKV 视角来理解一下 Heatmap:
- 模型已经学到的卷积层权重是 Query,模型预测的特征图 (C, H, W) 是 HxW 个 Key,这是一次 运算
- 而相比于完整的自注意力机制,计算得到的 Heatmap 本质上就是自注意力里的相似度矩阵,这是一个 的过程
- 于是我们自然会想到,如果把自注意力过程补全,加上多头和 V 的运算,加上交叉注意力里不同关键点之间的注意力,是不是可以提升 Heatmap 质量?欢迎有兴趣的同学尝试后告诉我结果
同样从 QKV 角度分析一下 SimCC:
- 模型预测的特征是 Query,模型已经学到的权重是 N 个 Key
- 所以 SimCC 跟 Heatmap 方法里,模型的 Query 和 Key 正好是反过来的
- 但是习惯上我们一般不把模型预测的特征作为 Query,所以如果强行套“学到的是 Query,预测的是 Key”,那么这是一个 的过程,默认情况下这里的 C 代表 HW,RTMPose 里通过全连接层对拉直的一维向量 HW 进行升维,本质上是增大 C
长远来看,Heatmap 方法上更接近于视觉信息的通用压缩思路的,更契合自监督等当下时髦的研究思路,更接近于所谓的“大道”,与其说它是一种定位算法,现在看起来定位功能反而像是视觉信息压缩算法的一个微不足道的“副产物”罢了:
- 一个强大的 Heatmap 方法监督得到的模型,提取到的像素 token,天生应该具备 zero-shot 和 few-shot 的关键点匹配能力
- 这也难怪 Heatmap 方法预训练的 Backbone 权重,在别的姿态估计方法(Regression,SimCC等)上都可以带来性能提升
而 SimCC 呢,反而更像是为姿态估计这个任务而设计的定位算法,模型所学的东西都是在为定位服务
- 而既然是在学习位置编码,那么今年 LLM 上对于位置编码的研究成果也都可以考虑一下如何结合到 SimCC 上
- 其计算流程与分类算法完全吻合,也意味着各种分类问题上的进展大概率可以来 SimCC 上试一手,各种蒸馏、剪枝、量化算法也是如此
- 考虑到 LLM 位置编码的外推性研究,SimCC 定位范式是否也可以考虑如何外推呢?毕竟当下的 SimCC 可是固定了输入图片尺寸,不能像 Heatmap 方法那样任意改变输入图片尺寸的
结语
Heatmap 方法作为姿态估计里最经典的算法,时至今日依然是中流砥柱地位,其简单的算法背后的思想总是让我常看常新。SimCC 作为后起之秀,在我看来是更适合姿态估计和一切定位任务的范式,能够服务于大量的计算机视觉子任务,目前似乎还没有被很多人注意到。
近段时间我的工作重心逐渐转到 LLM,后续应该也会开始输出一些大模型相关的笔记了,回顾一路走来关于 Deeplearning 的学习历程,姿态估计的学习过程就像是接受义务教育,现在我终于高中毕业了,也是时候去研究一些更深层次的知识了,相信之后以新的视角审视姿态估计,我同样能得到更多不同的感悟。
谢谢大家一直以来对我的关注和支持,我们今后继续一起努力~
如果你觉得我写的还有点意思,欢迎关注我的个人公众号:镜子的掌纹
都看到这里了,就点个赞再走吧~



 ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง
ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง


