导语
对称性支配着我们所在的世界,而我们的大脑会建立外部世界的模型,这自然引发一个问题:对称性是否也是大脑信息处理的基本原理?本文介绍了研究者近期发表的两篇NeurIPS工作,这些工作以空间平移和时间缩放两种变换为例,展示了神经系统对信息表征的对称性。具体而言,之前的一项工作用群论方法解析了神经系统实现空间平移不变表征的可能机制,最近这项工作用群论方法解析了神经系统实现一个序列活动(动作、发声等)快慢表征的可能机制。
关键词:对称性,神经动力学,群论 左峻枫 | 作者吴思Lab计算神经科学及类脑计算 | 来源
左峻枫 | 作者吴思Lab计算神经科学及类脑计算 | 来源
这项工作是和美国德克萨斯大学西南医学中心的张文昊教授(主要指导者)、美国加州大学洛杉矶分校的吴英年教授、以及课题组的刘潇同学合作完成。这项研究用群论(李群)方法解析了神经系统实现一个序列活动(动作、发声等)快慢表征的可能机制。在去年的NeurIPS文章中,我们也用群论方法解析了神经系统实现空间平移不变表征的可能机制。两个工作都是基于连续吸引子网络建模,并得到了一定的实验数据支持。用非常理论化的群论来阐明大脑的信息加工机制貌似有“牛刀杀鸡”之嫌(的确两次评审都有reviewer提出这样的疑虑,还好都被我们说服了),但我们坚信,在大脑信息加工机理方面这么多年研究进展缓慢、至今没有漂亮理论的今天,我们有必要做一些大胆尝试,即在参考已知实验数据的基础上,从纯理论的角度,对大脑工作原理做出大胆的猜测,而不必过分纠结于这个理论的实验支持;毕竟到目前为止,我们对大脑的精细结构和神经活动规律还知之甚少,一切可以留待以后再判断。在下面文章中,左峻枫同学对两篇NeurIPS工作进行了深入浅出的介绍。
大脑感知觉的对称性
在我们生活的世界中,对称性几乎无处不在。对称不仅存在于大自然中,也广泛存在于人造的建筑、美术、音乐中来赋予它们实用价值和艺术美感。比如我们每天早晨照镜子,镜子中的影像与我们互为镜像。再如一只海星的身体在72°的旋转变换下可以大致认为保持不变,一首卡农钢琴曲的某个声部也会在平移变换下与其他声部重合。通过以上例子我们可以看到,对称性意味着在某种变换下的不变性,比如虽然我们与镜子中的影像互为镜像(在此镜像作为一种变换),我们都知道这两个影像同属于我们自己(我们的身份保持不变)。值得注意的是,对称性不仅存在于日常生活的几何形态、物体特征这些简单概念中,还更深刻地存在于物理定律里面。这里物理定律的对称性是指物理定律在变换下的统一。例如我们观察真实世界和镜子中小球的运动,它们都满足牛顿运动定律,因此我们可以说牛顿运动定律在镜像中保持对称。这种广义的对称性催生了二十世纪物理学的革命,之后理论物理学家可以从基本的对称性出发直接推导和统一物理定律,而这也有了杨振宁先生那句名言:对称性支配相互作用(symmetry dictates interactions)。
既然对称性支配着我们所在的世界,而我们的大脑会建立外部世界的模型,那么这不禁让我们思考:对称性是否也能作为大脑信息处理的基本原理?值得注意的是,这里大脑的对称性并非大脑解剖结构上的简单形态对称,而是指大脑信息处理涌现的感知觉中的对称性。一些简单的思考能支持这个假说,比如我们可以轻易地想象出某个人与其镜像的影像,这意味着我们的大脑可以“创造”出这种镜像对称,说明这种对称性必然存在于大脑神经环路中。但对称性如何存在、表征在大脑神经环路中几乎是鲜有人问津的科学问题。因此这激励了我们近两年来的研究工作,即从广义的对称性出发,通过理论推导能实现该对称性的神经环路动力学,并且与具体的实验现象进行比较。我们目前的初步工作支持对称性作为大脑信息处理的底层“设计”原理。
群论:描述对称性的数学语言
对称性可以由群论(group theory)这门数学语言来严格描述。某一个群的对象是指某一类变换的集合,比如说所有的空间平移操作(移动1米、2米……)组成了一个平移群。同理,所有的旋转变换组成了旋转群,缩放变换组成了缩放群。照此类推在数学上存在很多群的结构。因此我们一般说的对称性是指在某个群变换作用下的对称。
我们通过一个简单例子让大家对群这个抽象的概念有一个直观感受。我们考虑s为二维的空间位置。同时我们考虑一个空间平移群,即所有空间平移变换的集合,而用表示空间平移群的一个元素,即为一个具体的平移操作,比如往东移动1米。若将所代表的平移变换具体作用在空间位置上时,我们数学上可以记为用一个具体的算符(operator)作用于:
这里表示群作用,而非算术中的乘法运算。直观起见,数学上我们可以用一个二维的向量来进行表示,而这里就相当于是一个二维的矩阵(图1左)。那么整个平移群就相当于是所有表示平移变换的二维矩阵的集合,你可以想象将无数多个二维平移矩阵堆叠在一起形成一个三维的结构(图1右)。之所以是无数多个是因为平移是连续变换,存在无穷多个。而在这个三维结构所表示的群里面,就相当于是在高度上某一层平移矩阵的索引号。值得注意的是,这里的二维矩阵表示以及群的三维数组表示并不总是存在,我们更多地是用这个例子让读者对群的抽象概念有直观感受。
我们知道外界刺激s是表征在大脑里面的群体神经活动中。我们用表示N个神经元在刺激呈现时的平均响应,即平均发放率,因此这里为一个N维的向量。数学上,我们可以把称为s的神经表征(neural representation),或者叫做将嵌入(embedding)在神经响应中。当用平移算符作用于外部刺激来得到时(式1),大脑中的神经响应也应当相对应地作出改变从而表征新的刺激。我们可以引入一个新的算符作用在神经表征上,
是作用于神经表征的算符,可以叫做“神经算符”;而是作用于刺激的算符。直观上说,因为是一个N维向量,则可以表示为一个维的平移矩阵,则为一个2*2维的平移矩阵。尤其注意的是,虽然和表面上的矩阵维度不一样,但是它们都代表了同样的群元素,这说明它们的内在(intrinsic)维度是一样的,这个内在维度是由群的结构所决定的。在数学分析当中,我们会理想化地假设有无穷多个神经元以简化数学分析,这时就变成一个连续函数,相当于一个无穷维的向量,而就变成一个无穷维的矩阵。
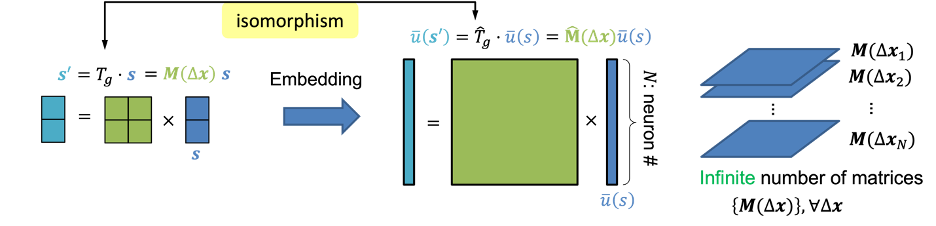 图1 矩阵表示下的群算符
图1 矩阵表示下的群算符
如果对于任意群元素,和任意的刺激式(2)都成立,即图2中红色和蓝色的路径结果一致,则就称为一个对群等变的表征。由式(2)可以看出,在等变表征下,神经算符的具体形式不依赖于被作用的刺激。仍然用平移来举例:用代表平移前的刺激,代表平移后的刺激,神经系统对的表征等价于算符作用在上。更进一步,作用在和时的形式完全一致,作用的效果都是使产生的平移量。具体而言,我们以空间平移群(Spatial translational group)和时间缩放群(Temporal scaling group)为例,从理论上设计了对应两种群变换的网络结构,其结果都与动物实验的结果相符合。
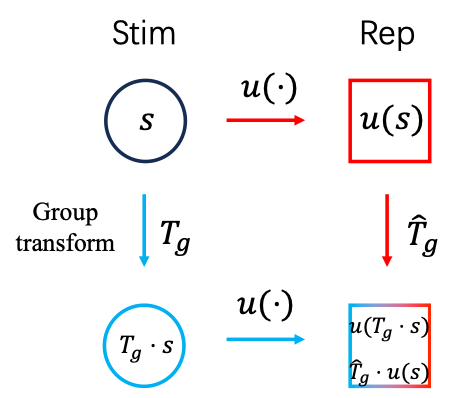 图2 等变表征和神经算符
图2 等变表征和神经算符
空间平移等变的网络模型
空间认知是动物生存最基本的能力之一。动物会在大脑中编码自身在空间中的位置,在空间中的运动就是对空间位置的平移变换。在[1]中,我们以一维情况为例,实现了一种网络结构,能够等变地表征空间位置,同时嵌入了能够对空间表征进行变换的平移算符。这个结果能够很好地解释果蝇的神经系统对方向的表征。
果蝇的罗盘系统
果蝇的神经系统能够十分准确地表征方向,而这一能力的实现要依靠果蝇大脑中的头朝向神经元。头朝向神经元的活动就好像罗盘的指针,指示着果蝇头部的朝向。当果蝇旋转时,这个“指针”也会随着一起旋转。
实验发现,果蝇的头朝向系统包含三个重要的部分[2](图3)。头朝向神经元构成一个环状的“表盘”,表示的角度,另有两群速度神经元分别表征向左和向右旋转的速度,分别为头朝向神经元提供一个略微错位的反馈输入。在这两群速度神经元的作用下,罗盘的指针被拨动,头朝向神经元对角度的表征就会随之平移。
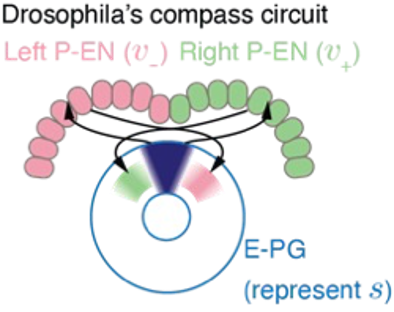 图3 果蝇的罗盘系统
图3 果蝇的罗盘系统
空间表征和平移算符
果蝇的罗盘系统可以很好地被群变换的语言描述。在这个例子中,表示当前的头朝向,的平移就代表头朝向的旋转。用表示头朝向神经元对角度s的响应,表示旋转的算符,则等变性要求。由于平移是一个连续的变换,我们需要特别地关注当平移量趋于无穷小时的无穷小变换g ̂的形式,随后任意有限大的变换都可以由连续地生成。因而也被称为空间平移群的生成元。具体地,我们可以用一个高斯波包来代表神经元的群体活动,波包的中心代表当前系统表征的位置。以神经元偏好的位置作为神经元的index,我们可以写出位置表征:
波包中心位置的移动与果蝇头朝向的转动相对应,如图4所示。
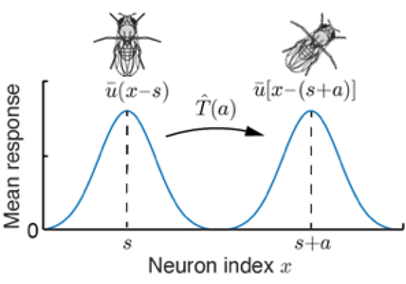 图4 波包平移与方向转动
图4 波包平移与方向转动
网络动力学实现
我们用连续吸引子网络来建模空间位置的表征。连续吸引子网络是一种特殊的循环网络,它的状态空间存在一系列连续的稳定解(图4的高斯波包),这一系列稳定解就构成对连续的空间位置的表征,可以很好地模拟头朝向神经元的活动。从群变换的角度出发,我们可以推出网络对角度的表征发生平移时网络动力学方程:
表示平移的速度,代表变换的生成元,二者一起构成了对角度表征进行平移的算符,使得沿着给出的方向和速度大小进行平移。
果蝇的罗盘系统启发我们,速度神经元对头朝向神经元的反馈可以起到平移算符的作用。因此,我们可以以更加生物合理的方式给出式(4)的实现:
是两群速度神经元活动的差值,其符号给出旋转的方向,绝对值给出速度的大小。由速度神经元对头朝向神经元的错位反馈实现,硬编码在网络连接的结构中。二者结合在一起,就能够动态地控制头朝向神经元对方向的表征,使其灵活地进行平移。
时间缩放等变的网络模型
我们生活的环境是一个动态的世界,在与外部环境交互的过程中,我们的大脑不断地接收来自外部的时序信息,同时向外输出一系列时间序列(如运动、说话、唱歌等)。在产生时间序列时,我们可以非常灵活地控制序列的时间尺度(即序列产生的速度),比如我们可以以不同的速度走路,可以用不同的节奏唱歌,但并不影响序列本身的内容。这种能力被称为时间缩放(Temporal-scaling),连续的时间缩放变换也能够构成一个时间缩放群。在这篇文章中[3],我们从时间缩放群的角度,构造出时间尺度缩放的理论框架,并搭建出一个可以对任意序列进行动态缩放的网络模型。
神经系统中的时间缩放
实验科学家已经对时间缩放进行了大量的研究,其中对记录到的大量神经元活动进行降维是一种常用的手段。在看到降维的结果之前,我们对不同时间尺度下神经元活动的低维轨迹有两种直观的猜测:第一种是,不同时间尺度下的神经元活动遵循同样的轨迹,只是沿轨迹运动的速度不同,所以最终得到的时间尺度不同;第二种是,不同时间尺度下的神经元活动轨迹长度不同,所以以同样的速度沿轨迹运动所需的时间不同[4]。已有的实验结果验证了第一种猜测。也就是说,在神经元的活动空间存在一个在时间缩放下保持不变的低维轨迹[5],这似乎隐含着某种对称性,这一点将在我们的模型中得到体现。除群体活动之外,单神经元的活动也存在缩放效果[5]。
实验上还观察到神经元活动和肌肉活动的解耦。[6]同时记录了猴子在不同时间尺度下的运动皮层神经元和肌肉的活动,经过分析发现,不同尺度下的神经元活动存在显著的相关性,即存在不变的低维轨迹(如前段所述),而肌肉活动在不同尺度下没有相关性。可见在时间序列输出的过程中,存在两个相互解耦的表征层次。这种解耦的特点提示我们,大脑中可能存在一个与具体序列无关的抽象时间表征,指导着不同序列的时间尺度。
时间缩放等变表征与算符
时间缩放变换也构成一个群。对应图1,不再是静态的刺激,而是一段时间序列,用表示,神经算符的作用对象也变成了神经活动序列。图3展示了时间缩放变换中时间、被表征序列以及对应的神经活动三个层次之间的等变性,三个层次上的时间缩放算符分别表示为,和,代表缩放因子,即时间缩放的倍数,t表示缩放后的时间。当时,序列被压缩;时,序列被拉伸;时,序列被反向。
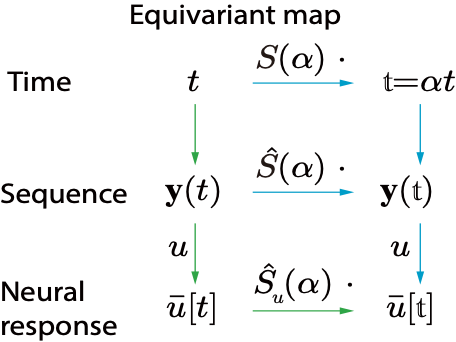 图5 时间、序列以及神经活动之间的等变性
图5 时间、序列以及神经活动之间的等变性
与前一个工作类似,时间缩放算符也应该能够由无穷小的生成元生成。还记得动物实验中发现,在不同的时间尺度下,神经元的群体活动中存在一个不变的低维轨迹,我们的模型也应该具有同样的结构,记这个低维轨迹为。我们猜想,神经元活动中的这一不变的轨迹,就代表时间信息在神经系统中的表征。由于我们只关心神经元活动沿这个低维轨迹的演化过程,因而我们就可以忽略其他方向的演化,将网络中的神经活动记为。
网络模型
参照实验中的发现,我们搭建了一个两阶段解耦的时间序列表征模型,如图4所示。第一阶段是一个循环网络,用网络中神经元的序列发放来表征时间信息;第二阶段是一个前馈网络,用于将循环网络产生的时间表征映射到对应的具体序列上,从而产生有意义的输出。用表示前馈网络的作用,整个网络就可以表示为:
得益于两阶段的解耦特性,我们仅需要让时间缩放算符作用在循环网络编码的时间表征上,就可以实现对输出序列的任意缩放。
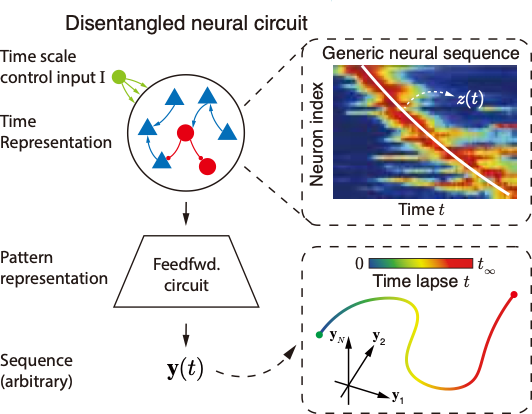 图6 两阶段解耦的时间序列表征模型
图6 两阶段解耦的时间序列表征模型
一维连续吸引子网络中嵌入了一个不变的一维流形,很好地对应于时间缩放中不变的低维轨迹,可以被称为“时间流形”。因而我们采用这一模型来建模表征时间的循环网络。为了让网络自发产生沿时间流形演化的序列,我们向网络中加入一个控制输入电流,如图4、5中的绿色圆圈所示。加入输入电流后的网络动力学表达式为:
等式右侧的前两项在稳定状态下相互抵消,而当网络状态偏离“时间流形”时,这两项会将网络活动拉回到正确的轨道上。与(5)式类似,(6)式中输入增益和输入电流两部分共同构成了时间缩放算符,像录音机的按钮一样,可以自由地控制输出序列“播放”的速度,也可以控制其“暂停”或“倒带”。
 图7 网络产生任意序列
图7 网络产生任意序列
实验结果
图8展示了时间表征部分在时间缩放变换下的结果,用于比较网络和神经系统的吻合程度。A图是单个神经元的活动在不同尺度下的缩放;B图对网络的群体活动进行降维,可以看到在低维上存在一个时间流形,其形状在不同的时间尺度下都保持不变(包括反向);为了更好地模拟生物体的情况,我们向网络中加入泊松噪声,结果发现,网络产生的序列长度的均值与方长呈现出线性相关,与生物的韦伯定律(Weber‘s law)相符,很好地验证了我们的模型。
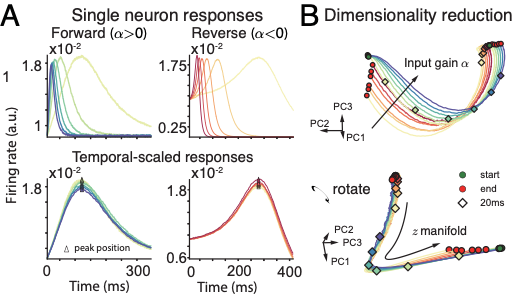 图8 时间表征的缩放变换结果
图8 时间表征的缩放变换结果
为了展示模型对任意序列进行缩放的能力,我们在一个手写数字的任务上对前馈网络部分进行了训练。在训练中,网络只学习在一个时间尺度下的序列。图9展示了网络在手写数字序列上的缩放能力。结果显示,一旦前馈网络部分学会了某个序列,就可以通过调节控制输入增益的方式对序列进行任意的缩放(包括反向)。
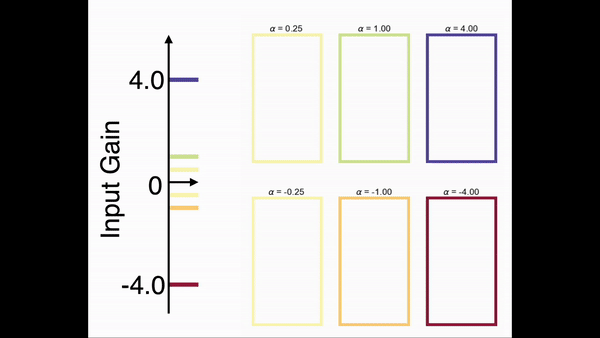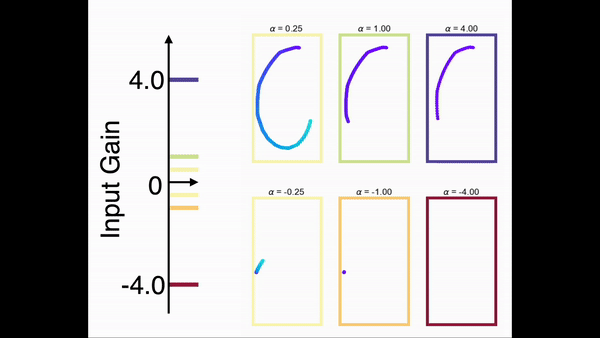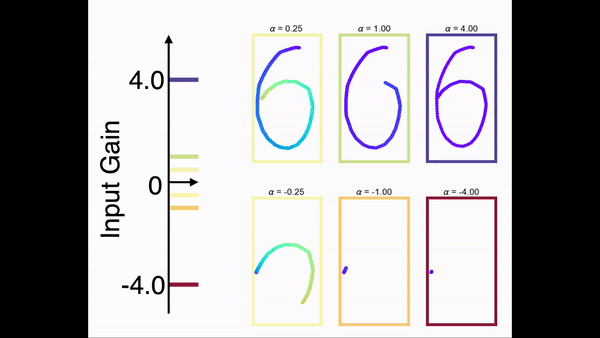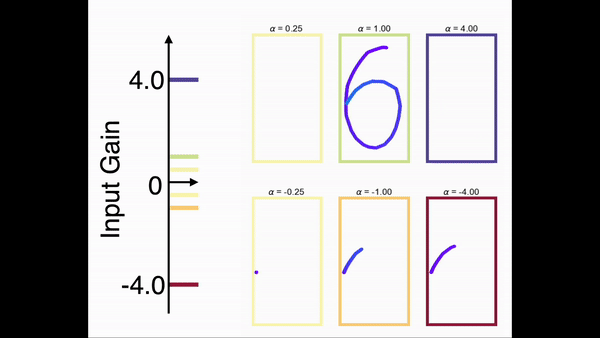 图9 任意时间序列的缩放,左侧的输入增益与右侧序列方框的颜色对应
图9 任意时间序列的缩放,左侧的输入增益与右侧序列方框的颜色对应
结语
本文以空间平移和时间缩放两种变换为例,展示了神经系统对信息表征的对称性。这种对称性包含两个方面:对外部变换等变的神经表征,以及对神经表征进行主动变换的神经算符,这基本上对应着动物和人类对外部世界的适应能力和交互能力。由于物理世界中存在广泛的对称性,我们有理由相信,生物在物理世界生存的过程中,很可能在大脑中采取同样的策略。未来我们将用对称性的语言更深入地探索大脑工作的原理。
参考文献
1. Zhang, W., Wu, Y.N. and Wu, S., 2022. Translation-equivariant Representation in Recurrent Networks with a Continuous Manifold of Attractors. Advances in Neural Information Processing Systems, 35.2. Kim, S. S., Rouault, H., Druckmann, S. & Jayaraman, V. Ring attractor dynamics in the Drosophila central brain. Science 356, 849-853 (2017). https://doi.org/doi:10.1126/science.aal48353. Zuo, J., Liu, X., Wu, Y., Wu, S. and Zhang, W.H., 2023. A Recurrent Neural Circuit Mechanism of Temporal-scaling Equivariant Representation. Advances in Neural Information Processing Systems, 36.4. Tsao, A., Yousefzadeh, S. A., Meck, W. H., Moser, M.-B. & Moser, E. I. The neural bases for timing of durations. Nature Reviews Neuroscience 23, 646-665 (2022). https://doi.org/10.1038/s41583-022-00623-35. Wang, J., Narain, D., Hosseini, E. A. & Jazayeri, M. Flexible timing by temporal scaling of cortical responses. Nature Neuroscience 21, 102-110 (2018). https://doi.org/10.1038/s41593-017-0028-66. Saxena, S., Russo, A. A., Cunningham, J. & Churchland, M. M. Motor cortex activity across movement speeds is predicted by network-level strategies for generating muscle activity. eLife 11, e67620 (2022). https://doi.org/10.7554/eLife.67620
神经动力学模型读书会
为了促进神经科学、系统科学以及计算机科学等多领域学术工作者的交流合作,吸引更多朋友共同探索脑科学与类脑研究,周昌松、臧蕴亮、杨冬平、郭大庆、陈育涵、曹淼、刘泉影、王大辉、刘健、王鑫迪等来自国内外多所知名高校的专家学者在集智俱乐部共同发起「神经动力学模型」读书会,历时四个月研讨,近日圆满结束。
本季读书会形成了聚集500+成员的神经动力学社区,积累了40+小时综述、解读、研讨的视频记录,以及多篇社区成员总结的词条、笔记、翻译、科普资料等。现在报名加入读书会,即可加入社区交流讨论(微信),并解锁相关视频、文本资料。我们对脑的探索才刚刚起航,欢迎你一道参与,共同点亮更多脑科学研究的岛屿!
详情请见:
500+神经动力学社区成员,邀你共同点亮更多脑科学研究的岛屿
推荐阅读
1. 大脑不对称性的起源:任务复杂性打破神经网络镜像对称性2. 脑网络通信综述:概念、模型和应用3. 脑与涌现的联系:从协同核到因果涌现4. 张江:第三代人工智能技术基础——从可微分编程到因果推理 | 集智学园全新课程5. 成为集智VIP,解锁全站课程/读书会6. 加入集智,一起复杂!
点击“阅读原文”,报名读书会





 ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง
ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง





