Global Optimization: A Machine Learning Approach
D Bertsimas, G Margaritis
全局优化:机器学习方法
-
使用机器学习方法求解全局优化问题,包括非凸和黑盒约束。
-
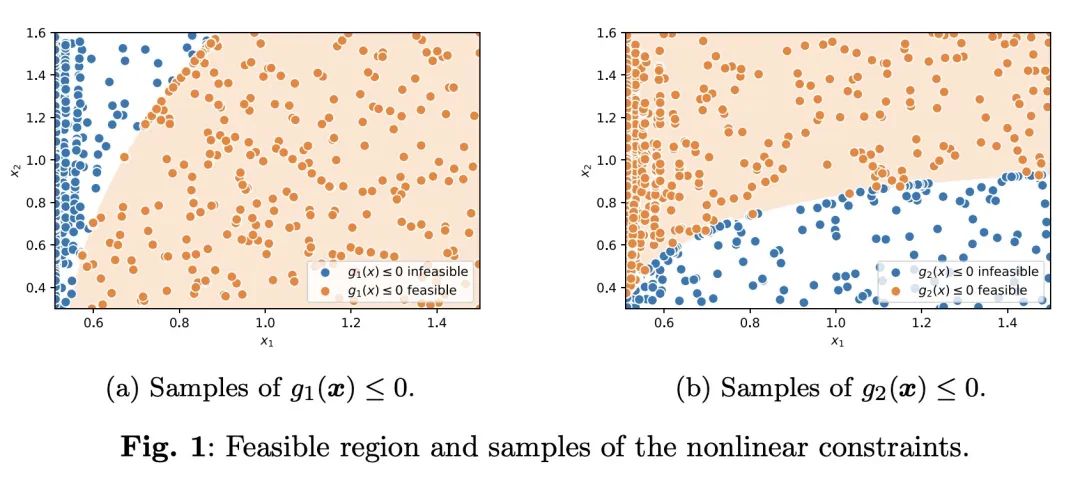
通过样本约束并训练机器学习模型(如SVM,GBM,MLP)来逼近非线性约束。
-
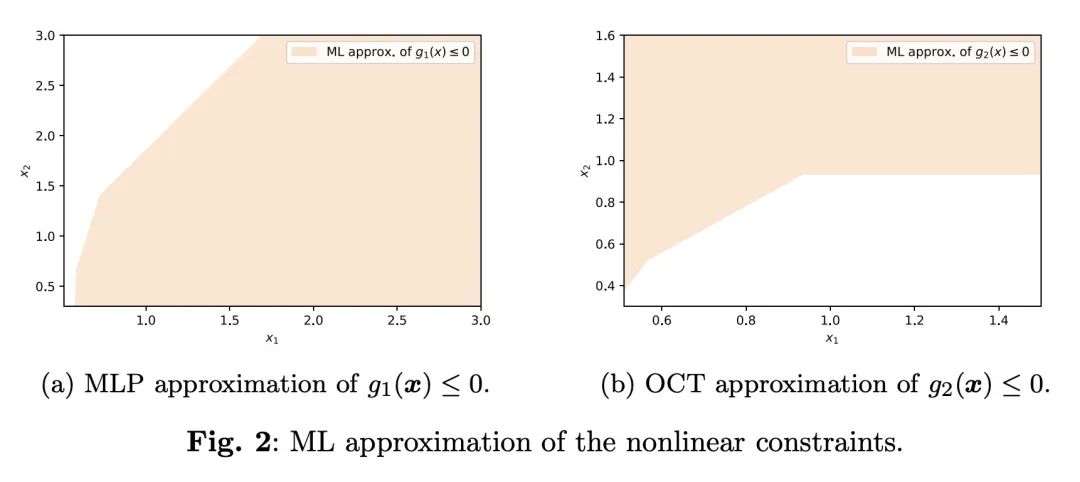
将训练好的机器学习模型表示为混合整数规划(MIO)约束,构建原问题的MIO逼近。
-
在MIO约束中引入鲁棒性,以处理机器学习模型训练的不确定性。
-
使用MIO松弛以处理逼近MIO的不可行性。
-
在81个全局优化问题基准测试中测试该方法,结果显示大多数情况下优化性能得到改进。
-
论文认为该框架是解决各类全局优化问题的有前景的通用方法。
动机:传统全局优化方法在处理黑盒约束、隐式约束或更一般的约束时存在限制,本文旨在提出一种结合机器学习和混合整数优化的方法来解决这些限制。
方法:提出一种名为OCTHaGOn的框架,通过使用基于超平面的决策树来近似非线性约束,并利用这些树构建原始问题的混合整数优化近似。论文还对该方法进行了扩展,使用了其他可表示为混合整数优化模型的机器学习模型,并提出自适应采样和鲁棒优化等方法来改进约束的近似精度。最后,论文在81个全局优化实例中测试了这个增强的框架,并展示了在大多数实例中解决方案的可行性和最优性的提升。
优势:该方法可以解决包括黑盒、隐式和更一般约束的全局优化问题,通过结合机器学习和混合整数优化,提供了更准确和高效的解决方案。
提出一种结合机器学习和混合整数优化的框架,通过近似非线性约束和改进优化算法,解决了全局优化问题中的约束限制和精度问题。
https://arxiv.org/abs/2311.01742





 ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง
ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง


