立冬 | 随机游走和电路

随机游走和电路，这两个问题看起来不相关，但却具有相似的数学结构。本文将从一维随机游走讲起，探寻其与电阻网络的联系，并将结论推广到图上的随机游走，量子游走，和布朗运动。

一个醉汉出了酒吧门，来到麦迪逊大道一街区，准备回到位于相隔四街区的家，但是到达一个街区后他只会随机选择一个方向前往下一个街区，一旦回到酒吧就不再出来，那么他今晚成功到家的概率是多少？这个问题可被建模为下图中的随机游走问题。[1]

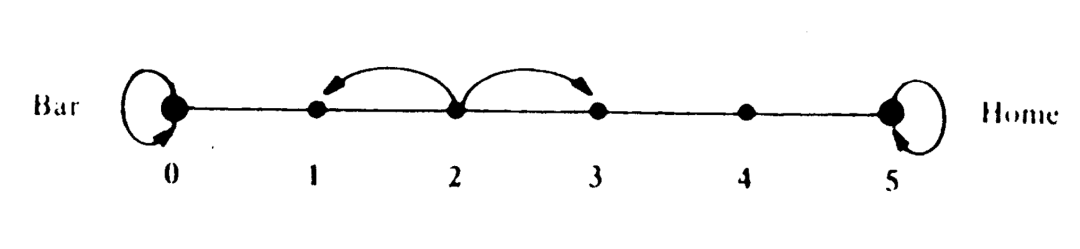
注意到醉汉没有记忆，到达一个街区后他不依赖已走的路选择前进方向，因此我们可以定义  为醉汉从  点出发，在到  点之前到达  点的概率，而  就是我们所要求的。对于  ，  满足这样的递推关系：

下一步到点从点回到家下一步到点从点回到家同时，  要满足边界条件 

这可以被看做一个“给定边界条件和函数性质，求在边界内函数值”的问题，实际上这就是物理中经常出现的迪利克雷问题（Dirichlet problem）的一维特例。

在求解这个问题之前，我们先考虑另一个问题：串联五个相同的电阻，并在两端加上 1V 的电势差，求点  点的电势。

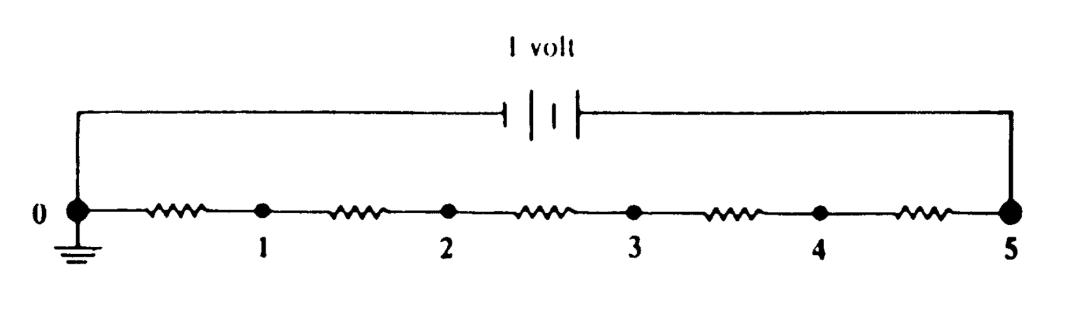
设  点电势为  ，根据题设，令每个电阻为  ，根据欧姆定律，点  到  的电流为  。根据基尔霍夫定律，  点流入流出电流和为  ，即对  ，有

也即对比发现，  和  满足相同的关系（等式  和等式  ）和边界条件（等式  和等式  ），那么我们是否有结论  呢？答案是肯定的。

首先我们证明对于定义在  上的函数  ，如果满足对于任意  ，

那么  的最大值和最小值一定在边界处也就是  和  处取到。证明的方式是反证法，如果  的最大值  只能在  中取到，不妨设为  。根据等式  ，  ，否则  和  中一定有一个严格大于  ，与  是最大值矛盾。对  递归使用这个推断，可以推出对所有  ，  ，这与  只能在  中取到矛盾。最小值的证明同理。

接下来，令  ，根据等式  和等式  ，  满足等式  ，因此  的最大和最小值在  和  上取到，而根据等式  和等式  ，  ，因此  恒等于  ，即  。通过对电流的计算，容易得到  。也就是流浪汉有  的概率在今晚回到家。

整理一下上面的分析，连接这两个的问题的桥梁是他们的解都满足等式  ，而我们证明满足等式  的函数在给定边界值的时候是唯一确定的。证明的关键是  个数中一定存在一个不小于其平均值的数。这个结论可以被推广为：对于  个数  和定义在其上的概率分布  ，一定存在一个  不小于其期望  。这给了我们一种直觉，上面的分析适用于更一般的情况。

对于更一般的随机游走，醉汉可以处在地点集  中的任意一个，当他处在  的时候，会以  的概率在下一时刻到达  （因此  需要满足  ）。酒吧  ，家  是两个特殊的地点，仿照前文，定义  为醉汉从  处出发，在到酒吧之前先到达家的概率，其满足  。可以证明对于任意  ，  等于其周围  的某种期望，严格来说，  满足

对于满足等式  的函数，我们称其在  上调和（harmonic）。对于任意  上调和的函数  ，给定  在  上的取值，如果以  作为转移矩阵的马尔科夫链是不可约（irreducible）的（一个较为宽松的条件），则可以证明  在整个  上的取值是唯一确定的。这个定理的证明类似一维情形，此处略去。

对于一般的电阻网络，假设  中的电阻为  ，根据基尔霍夫定律和欧姆定律其电势函数满足 即

也是调和函数。

因为电阻需要满足  ，所以在  是可逆的（reversible）时，即存在概率分布  使得 时，可以找到对应的电阻网络 使得等式  和  系数相同。这时如果给该网络加上电压使得  ，根据调和函数的唯一性，对任意  ，

总结一下，我们借由调和函数的桥梁，连接了电阻网络和随机游走。  在随机游走中和逃逸概率（escape probability），通勤时间（commute time），常反性（recurrence）有密切联系，也因此我们可以用电阻网络中的等效电阻（effective resistance）表示通勤时间，证明波利亚定理（  维格点上的简单随机游走在  时是常返的，否则是非常返的）。

另外，还可以证明  等于从  出发在到达  之前经过  的期望次数，而从  流到  的电流满足 其中  是从  到  经过  的期望次数，  是从  到  经过  的期望次数，这就给了电流一种符合直觉的概率解释。

在最近的工作 [2][3] 中，量子游走从点  出发找到  的期望时间被证明正比于  ，其中  是  和  的通勤时间，也就是从  出发随机游走到  再返回  的期望时间。而有趣的是，因为量子游走和经典随机游走存在较大差异，结果中出现的  在分析中不是通过与经典随机游走的类比得到的，而是借助电阻网络作为桥梁间接得到的。

搭起这座桥的方式是观察到与  正交的量子态可以被写成

其中  满足基尔霍夫电流定律。与  正交意味着是量子游走算符特征值为  的特征向量，该特征空间在量子游走相关的算法中扮演着重要角色。

我们上面考虑的都是离散情形，如果时间和空间都是连续的那情况会如何呢？连续情况下，我们称满足如下方程： 的二阶连续可微函数  为调和函数。方程  被称为拉普拉斯方程（Laplace’s equation），在物理中有广泛应用，无源场中的电势，无热源的稳态热传导系统都满足拉普拉斯方程。

而我们上面列出的方程  就对应于连续情况的一维拉普拉斯方程 方程  对应于连续情形调和函数的平均值性质的推广。连续版本的随机游走：布朗运动（Brownian motion）也与调和函数有着密切的联系。

References:

[1] Doyle, Peter G., and J. Laurie Snell. Random walks and electric networks. Vol. 22. American Mathematical Soc., 1984.

[2] Ambainis, Andris, et al. “Quadratic speedup for finding marked vertices by quantum walks.” Proceedings of the 52nd Annual ACM SIGACT Symposium on Theory of Computing. 2020.

[3] Belovs, Aleksandrs. “Quantum walks and electric networks.” arXiv preprint arXiv:1302.3143 (2013).

文 | 王昕兆

图 | 除标注外，源自网络

—   版权声明  —

本微信公众号所有内容，由北京大学前沿计算研究中心微信自身创作、收集的文字、图片和音视频资料，版权属北京大学前沿计算研究中心微信所有；从公开渠道收集、整理及授权转载的文字、图片和音视频资料，版权属原作者。本公众号内容原作者如不愿意在本号刊登内容，请及时通知本号，予以删除。