
导语
为什么小小的跳蚤可以跳得那么高?为什么小到细胞内部的线粒体、大到蓝鲸,都遵循同一套定律?为什么80%的财富被20%的富人所占有?为什么“黑天鹅事件”的可能性比我们想象的大很多?这一切都与尺度,也就是规模有关。定量研究发现,生物大小、城市规模、公司寿命,背后都遵循同一套规模法则。今天的文章节选自北京师范大学系统科学学院教授、集智俱乐部创始人张江老师的新书《规模法则:探索从细胞到城市的普适规律》第二章。
本周四(11月16日)中午13:00-14:30,张江老师将与一土教育联合创始人华章老师进行对谈,讨论教育内卷、人工智能未来、城市生态未来等话题,希望看到这些复杂现象背后的规则。本周六(11月18日)集智俱乐部「复杂系统管理学读书会」也将开启一段《规模法则》的探索之旅,由智慧足迹数据科技有限公司经济研究员张力钧,以及联合分享人张德伟共同主讲,探索《规模法则》在组织管理等领域的新方向。欢迎感兴趣的朋友关注,详情见文末。
研究领域:规模法则,分形,幂律分布,异速率,克莱伯定律 作者简介
作者简介

张江:北京师范大学系统科学学院教授,集智俱乐部、集智学园、集智科学研究中心创始人,曾任腾讯研究院、华为战略研究院等特聘顾问。主要研究领域包括复杂系统分析与建模、规模理论、机器学习等。
新书试读:万物的规模
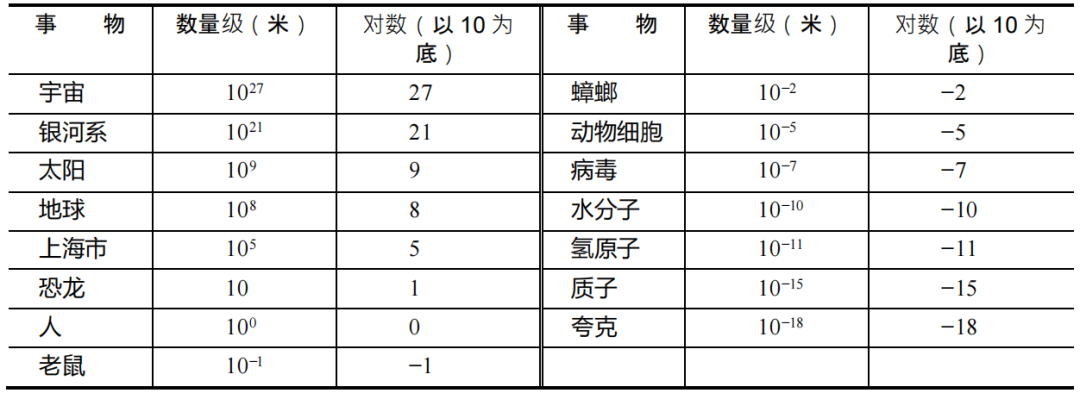
万事万物都有尺度,也就是规模。规模通常是相对而言的,没有参考的基准,就没有了比较的可能,也就失去了意义。不同量的比较基准构成了量纲(dimension),米、秒、千克都是基本的物理量纲。大千世界中,不同事物的规模差异是如此之大。如表2.1所示,就人类现有的科学技术所能观测到的最小事物和最大事物来看,规模横跨了45个数量级。由大量个体组成的复杂系统也有其规模,但这些规模可能不可见,例如互联网社区和鸟群。对于这样的系统,我们通常用其包含的个体数目作为系统规模的基本度量。
表2.1 万物的规模
1. 尺度
图2.1分别展示了不同尺度下原子、细胞、皮肤和星系的样子。当通过缩放自身的比例大小来遨游宇宙的时候,我们将会经历非常奇特的尺度比例之旅[1]。最重要的是,你身处的空间点在整个规模缩放的旅程中可能丝毫没有变化。这就像科幻电影《蚁人》中的情节一样,主人公乘坐尺度飞船从正常人的尺度穿梭到原子的尺度,周遭事物发生了天翻地覆的变化,但有趣的是一切都发生在同样的空间点上。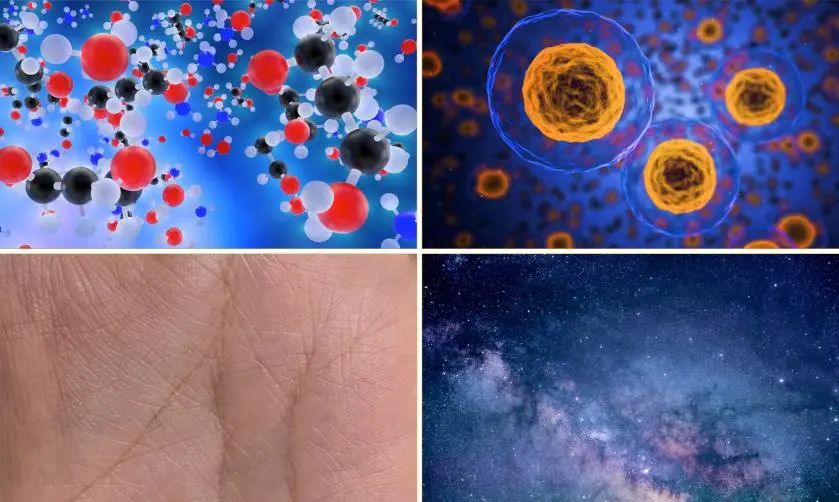 图2.1 不同尺度下的事物形态(除皮肤外的图片来自pixabay)
图2.1 不同尺度下的事物形态(除皮肤外的图片来自pixabay)
与空间类似,时间也有其尺度。一段时间的长度就是时间的尺度。有些过程发生的时间很短,例如原子的核裂变;有些过程发生的时间很长,例如星系的形成。不同的时间尺度会呈现完全不同的景象。例如,从人类熟悉的时间尺度来看,植物大多数时候“呆呆傻傻”,没有发生有趣的生命行为;但是从更大的时间尺度来看,植物的生死过程却短得可怜。
尺度是一类观察事物的独立变量。我们已经熟悉了用四维空间中的点来表示某一个事件,但实际上,由于在不同尺度下看到的事物会非常不同,因此我们可以把尺度作为一个新的坐标引入对事物的描述之中。例如同样是死亡这个事件,细胞的死亡和人体的死亡发生在完全不同的时间、空间和尺度之下。
一个系统的尺度往往决定了它的功能、特性等。尺度不仅仅取决于事物本身,还与比较对象有关。例如,蚂蚁无法和大象比较力量,因为它们处于完全不同的尺度量级;大公司的管理方法跟个体户的管理方法不同,因为它们处于不同的规模量级;夸克级别的量子规律也不能简单外推得到分子级别的化学规律,因为它们处于不同的尺度量级。正如达西·汤普森(D’Arcy Thompson)著的《生长和形态》一书中所说:“天下之大,事物的规模都逃不过自然之手。万事万物都有各自合适的尺寸。人和树、鸟和鱼、星星和星系,都有一定的大小,其绝对量值也是有限的。人类观察和体验的范围也只限于厘米、米和千米这样狭小的领域,这一切都是以人类自我意识和自我行为的语汇来度量的。至于光年、秒、埃、原子或亚原子单位这样的尺度,则属于另一类事物和另外的认知方法。”
规模是一个具体事物的尺度,也是复杂系统中最显著的变量,它忽略了大量的细节信息,却可以展现出很好的规律性。接下来展示一个小例子,由此可以看到不同城市规模背后的规律性。我们考虑美国所有的城市,并用城市的总人口作为该城市的规模度量。我们将所有的城市按照规模从大到小进行排序,并把每个城市的规模和排名画在一个双对数坐标系(横纵坐标轴上等间隔排列的刻度是数量级的对数)中,就会得到图2.2。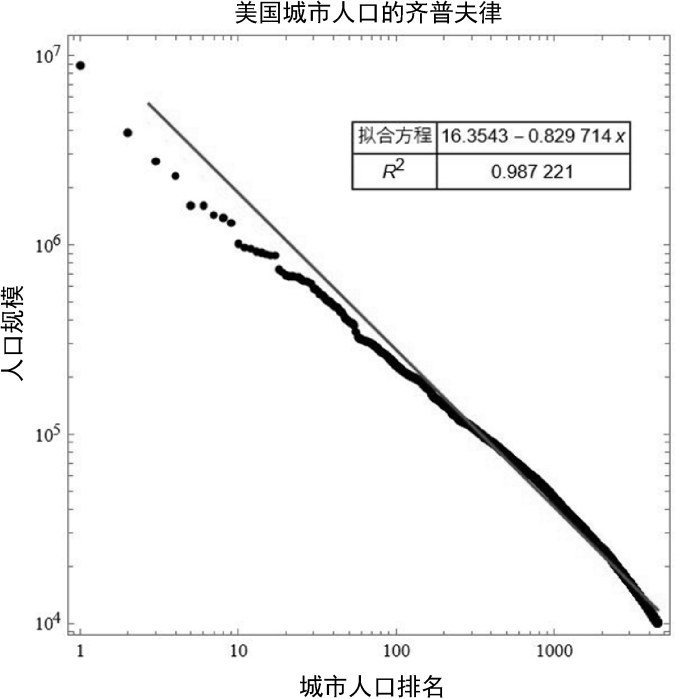
图2.2 美国城市的齐普夫律,城市人口数据从mathematica软件提供的免费在线数据库获得
数据点近似形成一条直线,通过拟合可以得到其斜率是−0.83,这表明:
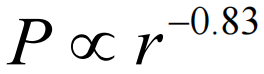 (2.1)
(2.1)
其中P为城市人口,r为以人口为标准的城市排名。式(2.1)意味着美国最大城市的规模是第二大城市的1.8(20.83)倍,是第三大城市的2.6(30.83)倍……而排名第100的城市规模是排名第200的城市的1.8倍。这意味着排名靠前的大城市规模差异非常大,而排名靠后的小城市规模差异却很小。总体来看,美国城市的规模分布极其不均匀,存在大量规模差异不大的小城市,以及少数规模差异巨大的大城市。
城市人口和排名呈现出清晰的幂律关系,这一规律被称为齐普夫律(Zipf’s law),它反映了城市人口分布的不均匀性。研究者发现人们的财富水平、单词使用频率、地震强度等也都满足这一规律。由此可见,复杂系统的规模下蕴藏着深刻的规律性和普适性。这就是为什么我们要从规模入手来研究各类复杂系统。
2. 规模缩放
相信你一定使用过家用摄像机或者手机上的摄像头。摄像机上有一个放大(zoom in)及缩小(zoom out)焦距的旋钮,调节它就可以成比例地放大或缩小一个东西的观测尺度,我们把这种放大或缩小的动态过程称为规模缩放,即按照比例放大或缩小物体。英文scale一词作为名词时,拥有尺度、比例、度量等意义;作为动词时,它表达的是规模缩放。于是,作为scale的动名词形式,scaling一词表达的就是规模缩放这一动作。
我们可以利用摄像机进行一个有趣的小实验,从而窥探尺度、规模缩放与复杂性之间的联系。找来一台电视机和一台摄像机,将摄像机的视频输出连向电视机的视频输入,然后用摄像机拍摄电视机屏幕,并将屏幕上的画面通过摄像机-电视机回路实时播放到电视机屏幕上,这就构成了一个摄像机-电视机的视频反馈回路,如图2.3所示。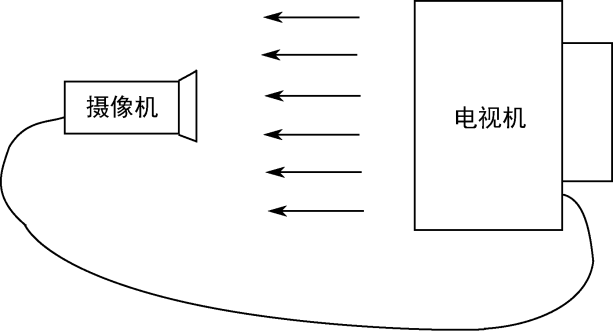 图2.3 摄像机-电视机的视频反馈回路
图2.3 摄像机-电视机的视频反馈回路
此时电视机屏幕上会出现一条蜿蜒的长长的“走廊”,走廊尽头有一个小小的白色亮点,它代表着这个虚拟空间中的“无穷远点”。更有趣的事情还在后面。当我们慢慢调节摄像机上的旋钮,对准屏幕中心的小亮点,不断地放大它……当放大到一定比例的时候,我们会看到,一些复杂的结构、花纹会从屏幕中心“飞出来”,如图2.4所示。这相当于一个不断自动规模放大的过程,而被放大的东西就是无穷“走廊”中的那个“无穷远点”。当这个“无穷远点”放大到一定比例时,就会“喷发”出一系列复杂的结构,有的像岛屿,有的像星系。更有意思的是,当摄像机歪斜一定的角度,这些复杂的结构会发生相应的旋转,转动旋钮放大的比例越大,这些结构奔涌出来的速度就越快。当换用不同的摄像机或电视机重复这个实验的时候,你会看到完全不同的结构。这些结构与设备相关,似乎越古老的设备越能展现出有意思的动画。例如,模拟摄像机比数字摄像机更容易展现出漂亮而复杂的动画。
图2.4 摄像机-电视机的视频反馈画面。更多关于这个实验的说明,可以参考维基百科“摄像机-屏幕自指实验”,更多视频见B站“摄像机自指实验”
事实上,整个系统就是一个视频反馈回路,规模缩放操作会不断地作用到屏幕自身上。在这样的条件下,摄像机-电视机的视频反馈回路所产生的噪声信号会被放大(就像话筒对准音箱所产生的啸叫),这正是那些复杂动画产生的原因。
在此,我们并不打算对这个实验背后的原理展开更多的讨论,而是希望用它形象地展示规模缩放与复杂性之间的联系。
3. 缩放对称与分形
规模缩放是一种几何变换,就像是空间中的平移变换和旋转变换一样。在几何变换下,我们常常关注某种不变性。以空间平移变换为例,如果一个几何体在平移变换下不变,那么我们就说这个几何体具有空间平移对称性,比如直线。圆还具有旋转对称性,因为无论从哪个角度来看,圆都是一样的。
与此类似,对于规模缩放变换来说,如果一个几何体在不同缩放比例下观察起来没有任何区别,那么我们就说这个几何体具有规模缩放对称性,简称缩放对称性。什么样的几何体具备这种特性呢?直线很显然是缩放对称的,因为无论将其放大多少倍,它还是一条无穷长的直线。与此类似,一个无穷延展的平面也是缩放对称的。除此之外,人们还发现了一大类几何体具备这种缩放对称性,这就是分形(fractal)[2]。分形一词最早由法国数学家曼德尔布罗(B. B. Mandelbrot)提出,用来描述一系列形状不规则,但具有缩放对称性(或称为自相似性质)的几何体。如图2.5所示的分形雪花,它在缩放变换下体现出不变性:将它的局部线段放大就会发现,它与整体曲线自相似[3]。不仅仅是人造几何体,自然界中也存在大量的分形现象,包括云朵、菜花、树木。分形几何的一个核心思想就是缩放不变性。 图2.5 分形雪花
图2.5 分形雪花
4. 规模法则
既然尺度可以看作一种与时间和空间同等重要的变量,那么我们就来看看当系统的规模发生变化时会发生什么。我们可以考察系统其他变量如何随着规模而改变。比如,把一个三角形扩大2倍(把每条边的长度都扩大2倍),那么其周长也扩大了2倍,而面积扩大了4倍。一般地,设三角形扩大了x倍,那么周长扩大x倍,面积扩大x2倍。这种在规模缩放下不同量之间展现出来的幂律关系称为规模缩放法则(scaling law),简称规模法则。
三角形中,周长会与边长同比例缩放,我们称这样的规律为“同速规模法则”(isometric scaling law)。当三角形变大的时候,面积显然会比边长增长得更快(以平方的速度增长),我们称这样的规律为“异速规模法则”(allometric scaling law)。
一般地,如果某变量Y随着系统规模M的变化关系可以描述为幂律函数:
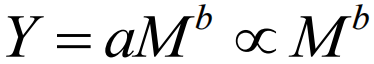 (2.2)
(2.2)
则我们称Y满足规模法则。式(2.2)中,b为规模法则的幂指数,a为规模法则系数。式(2.2)中等号右边写成了“成比例于”(∝)的形式,因为在很多讨论中,我们并不关心系数a,仅仅关心幂指数b,式(2.2)正是忽略a的形式。
将式(2.2)的两边取以e为底的对数,就会得到:
lnY = lna + blnM (2.3)
如果将lnY和lnM看成两个变量,那么式(2.3)就变成了一个线性方程。如果把曲线画在lnY与lnM的坐标系(也就是上文所说的双对数坐标系)中,它就变成了一条直线,其中b是这条直线的斜率,lna是截距。在实际的数据分析中,我们通常将数据画在双对数坐标系中,然后通过线性回归拟合数据,从而计算出a、b的数值。
5. 规模法则举例
观察式(2.2)会发现,所谓的规模法则就是一个幂律方程。我们知道,数学、物理中的幂律方程比比皆是,比如牛顿力学、库仑定律、面积公式、体积公式等都可以写成幂律方程的形式。那么,是不是只要是幂律方程,就一定意味着规模法则呢?
答案是并非如此。规模法则的实质是规模缩放,进而通过考察各种变量如何随着规模缩放的尺度系统性地变化,就可以把握系统的关键因素和规律。我们来看一些具体的例子,有的跟我们的日常生活密切相关,有的牵扯到一些热点新闻事件,有的还关系到重要的科学问题。
5.1 比萨
假设某天你走进比萨店,点了一个直径为9英寸[4]的比萨并付款。经过几分钟的等待,店员突然走过来跟你说:“抱歉,9英寸的比萨已经卖完了,我给您换成两个5英寸的吧?”那么,你该不该接受店员的建议呢?
这个问题看似很简单,两个5英寸的比萨加起来好像是一个10英寸的比萨,比一个9英寸的还大,你可以占点儿小便宜。但其实这个建议对你非常不划算。因为两个直径为5英寸的比萨的总面积要小于一个直径为9英寸的比萨!为什么会这样呢?答案就在于简单的规模法则:
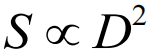 (2.4)
(2.4)
其中D为比萨的直径,当它变成了原来的1/2时,面积减少为原来的1/4,而不是1/2。因此,两个5英寸比萨的总面积还不到一个9英寸比萨的2/3,如果你接受店员的建议,就吃了亏。
我们之所以在这个简单的问题上很容易犯错误,是因为人脑非常擅长线性外推。当我们听到店员的建议之后,大脑就会下意识地认为两个5英寸比萨的总面积等于10英寸比萨,而不会按照式(2.4)的非线性规模法则进行思考。这种例子在生活中还有很多,不懂得非线性规模法则经常会让我们闹出很多笑话,然而下面的例子就没那么好笑了。
5.2 从服药剂量到假疫苗事件
假设你家有两个宝宝,大宝8岁重25千克,二宝两岁重12.5千克。如果大宝感冒需要一次喝两包感冒冲剂,那么二宝感冒需要喝多少呢?一包吗?
答案并不是一包,而是一包多一些。为什么要喝这么多呢?根据下一章即将介绍的克莱伯定律,生物体的代谢率和体重呈幂指数b=3/4的幂律关系。这意味着,体重减少一半,代谢率并不会下降一半,而是变为原来的60%左右。人类对药物的消化能力主要来源于代谢能力,所以合适的剂量应该减小为原来的60%左右。
这又是生活中的一个非线性规模法则的例子,而我们却很容易犯线性外推的错误。即使是相关技术人员,也有可能无法避免类似的情况。比如,2018年夏天闹得沸沸扬扬的长春长生假疫苗事件,就很有可能是操作人员忽略了从“小罐发酵”到“大罐发酵”这一规模放大过程中的非线性效应而导致的。一般的制药和发酵行业(尤其是制药行业)在从实验室研究到大规模生产的过程中,要经历实验室规模、小试、中试以及正式生产这样的规模放大过程。每个阶段都需要突破大量的技术瓶颈,才能获得与前一个阶段同等质量的产品,而非简单地等比例增大用量。因此,总是需要严格地进行各项试验,才能够提高产率并通过检验。长生制药的工作人员在没有经过审批的情况下更换更大体积的发酵罐,结果引起了产率下降、毒素水平升高等问题。
再比如,1962年,科学家要在大象身上试验一种致幻剂LSD的效果。他们想当然地把在猫身上的安全剂量等比例地用到了大象身上,结果酿成了悲剧。LSD在猫身上的安全剂量差不多是0.5毫克,而他们的试验对象亚洲象图什科重达3吨,这个重量大概是猫的600倍,于是计算得出用量为300毫克,实际的注射量是297毫克。注射5分钟后,可怜的图什科开始大声尖叫,并轰然倒下、失控排便、进入癫痫状态,差不多1小时40分钟后,可怜的图什科不幸身亡。人们对非线性规模法则的无知就这样杀害了这头可怜的大象!
5.3 大城市其实更危险
现在,很多大学毕业生向往留在大城市,因为大城市能够提供更多的发展机会。然而,人们往往会忽略一个事实:大城市的犯罪率比小城镇更高,即每个人平均遭遇犯罪活动的可能性会更大!圣塔菲研究所(Santa Fe Institute)的学者路易斯·贝当古(Luis Bettencourt)利用美国各大城市的犯罪率数据和人口数据得到了如下超线性规模法则:
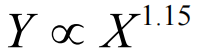 (2.5)
(2.5)
其中Y为一个城市中一段时期内发生犯罪活动的总数量,X为城市的总人口,超线性规模法则是指这两者的幂律关系的指数b显著大于1。这意味着城市越大,总的犯罪活动也会越多。根据式(2.5),我们还可以得到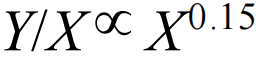 ,这意味着城市越大,平均每个人遭遇犯罪活动的可能性就会越大。大都市并不是只有亮丽光鲜的摩天大楼,也有其黑暗的一面。
,这意味着城市越大,平均每个人遭遇犯罪活动的可能性就会越大。大都市并不是只有亮丽光鲜的摩天大楼,也有其黑暗的一面。
5.4 为什么跳蚤可以跳得这么高
普通人的跳跃高度在50厘米左右。跳蚤的体长在0.5毫米到3毫米,却可以跳跃35厘米的高度,这足足是其体长的100倍到700倍,这怎么可能呢?事实上,早在16世纪,伽利略就根据力学中的规模法则得出了生物体跳跃的高度与其体长无关这一结论。所以,跳蚤能跳跃自己体长数百倍的高度一点儿也不稀奇,但这是为什么呢?
我们知道,决定跳跃高度的因素包括腿部弹跳力量大小和体重大小。决定弹跳力量大小的是大腿支撑的应力,该力正比于腿部横截面积,这一面积则正比于体长的平方,而动物的体重显然正比于体长的立方。当身体变小的时候,腿部力量和体重虽然都在减小,但是后者减小得更快,这样跳蚤的弹跳高度与体长的比值就要比人类大很多。
更具体地,动物弹跳需要克服重力做功,这部分能量只能由动物自身肌肉收缩舒张做功得到。假设动物弹跳力量大小为f,它在跃起过程中腿部移动的距离为l,这样弹力做功与fl呈正比。而体重为m的动物,若要完成高度为h的跳跃,需要克服重力做功的大小为mgh,g为重力加速度。显然,这两部分能量应该相等,即fl = mgh,于是h = fl/(mg)。
如果动物体长为L,则体重m∝L3,应力f∝L2,做功长度应该与体长呈正比,即l∝L,于是:
h∝L0 (2.6)
这是一个特殊的规模法则,其幂指数刚好为0,也就是说,动物跳跃的高度实际上与它的体长无关。这就解释了为什么跳蚤跳跃的高度可达35厘米,这和普通人的跳跃高度没有差太多。如果我们将跳跃高度比上动物的体长,则得到一个具有负幂指数的规模法则:
h/L∝L-1 (2.7)
也就是说,动物越小,它相对于自身体长的跳跃高度反而会越大。
6. 规模分析简史
跳蚤跳高的例子展现了规模分析的强大威力。规模分析(scaling analysis)是研究事物在规模缩放变换下展现出来的特性,或者据此做出某些判断。这是与我们熟悉的分析物体的时空运动特性(例如微分方程)相并列的另一种方法。如果我们深究规模分析方法的历史,会发现它几乎跟物理学的历史一样悠久[5]。
规模分析方法可以追溯到16~17世纪的伽利略。伽利略被称为“物理学之父”,他同样也是规模分析领域的鼻祖。他很早就利用力学中的规模法则来分析生物体的各类特性。他得出了随着体型的增长,动物的四肢会变得短粗,整个骨架也会更加壮实、沉重的结论。伽利略甚至预言了树木的最大高度为90米,这与实际观测到的最高杉树的高度非常接近。
到了18世纪,著名医生勒萨(Leasage)在一本未公开的著作中,运用类似的分析方法得出了昆虫和一些小型陆生动物长有厚而硬的皮肤的推论。这是因为,动物对水分、养料的消耗速度与它们的表面积和体重之比有关。我们知道,动物变大的时候,体重比表面积增长得更快,所以越小的动物,表面积和体重之比越大,它们的水分越容易散失,所以不得不进化出厚厚的表皮加以保护。
后来,人们运用同类型的方法,分析了生物体的各种变量,包括运动速度、代谢率、跳跃高度、行走的摆动幅度等与生物体体积的关系。这些都是早期发现的异速律,即规模法则,但是那时的人们并没有使用这一名字。人们也将这套方法运用于力学问题中,例如桥梁、宫殿等建筑物需要用粗大的柱子加以支撑,也是基于同样的考虑。
1822年,著名数学家、物理学家约瑟夫·傅里叶(Joseph Fourier)将这套方法进一步提炼,提出了量纲分析(dimensional analysis)的初步思想。他指出,基本的物理定律,比如牛顿第二定律F = ma,不应该因为这些物理量所选取的量纲不同而具有不同的形式。也就是说,用米、分、千克作为量纲和用厘米、秒、克作为量纲,应该得到同样形式的牛顿定律。量纲分析蕴含着规模分析的思想,因为选取不同的量纲实际上等价于在物理量上乘了一定的比例系数,也就相当于对该物理量进行了规模缩放变换。例如,我们将牛顿第二定律中的质量m的量纲由千克换成克,则相应的m的值就应该扩大1000倍。因此,物理公式要在量纲变换下保持不变,相当于要求该公式在规模缩放变换下保持不变。后来,这套方法被贝特朗(J. Bertrand)、白金汉(E. Buckingham)等人进一步提炼总结,形成了现代的量纲分析方法。目前,量纲分析已经成为物理学和工程中的一种重要的分析方法。它往往能够在我们对研究对象性质不熟悉的情况下,迅速找到起主导作用的变量。
1917年,生物学家达西·汤普森出版了他的旷世名作《生长和形态》(On Growth and Form),该书列举了大量采用量纲分析、规模分析的手段研究生物体的例子,并进行了总结。同时,该书还就生物体如何生长以及生物体展现出来的各种几何形态进行了广泛讨论。
1932年,化学家马克斯·克莱伯(Max Kleiber)系统性地研究了哺乳动物新陈代谢率与其体重的关系,并发现异速规模法则幂指数是3/4,而不是1882年鲁布纳(Rubner)通过量纲分析得到的2/3,因此提出了克莱伯定律。前面的分析大多借鉴物理学的手段,例如受力分析或者量纲分析;被分析的对象也大多是标准的欧氏几何体。生物体的新陈代谢牵涉到其内部运作机制,是非常复杂的生物、化学、物理过程,而且3/4这一幂指数的发现也在向我们暗示生物体的分形几何特性。因此,克莱伯定律具有划时代的意义,它首次将规模法则拓展到了复杂系统之中。
异速律(allometry)一词最早由生物学家赫胥黎(Huxley)和泰西耶(Tessier)在1936年开始使用。他们研究招潮蟹(fiddler crab)的钳子大小是如何随着其身体大小变化的,发现两者之间存在幂律关系。20世纪初,路德维希·冯·贝塔朗菲(Ludwig von Betalanffy)等人对有关生物体的规模法则研究进行了扩展,进一步对生物体的异速规模法则进行了分类,包括种间异速规模法则、种内异速规模法则以及个体发育异速规模法则。也就是说,当对生物体的异速规模缩放现象做统计分析的时候,我们既可以针对不同的物种来统计,也可以针对某一个物种的不同个体来统计,还可以针对同一个个体的不同发育时间段来统计。这就是这3种法则的区别。人们对生物体的规模法则有了系统化的认识,并创作了大量的文章和图书。
20世纪五六十年代,在贝努瓦·曼德尔布罗(Benoit Mandelbrot)等人的努力下,分形几何成为大家熟知的重要概念。如前所述,分形就是一种在规模缩放变换下保持不变的几何体。曼德尔布罗发现,这些分形几何体本身就存在很多规模法则,例如图2.5所示的分形雪花的周长就和它的直径存在规模法则,幂指数甚至可以用来定义几何体的分形维度。分形与规模法则以及规模分析方法存在密切的关系。而且,很多规模法则的起源可以追溯到分形几何的特性,例如著名的克莱伯定律就被认为起源于生物体内部的分形输运网络——参见本书第3章。
幂律分布(power law distribution),或更准确地称为厚尾分布(fat tail distribution),是另一种形式的规模法则,它刻画了事物出现的概率与事物的规模呈现负指数的幂律关系。这种概率分布表明,出现“黑天鹅事件”的可能性要比我们想象的大很多。例如,早在19世纪,著名经济学家帕累托(V. Pareto)就发现社会财富分布服从幂律形式,即80%的财富被20%的富人所占有。其中超级富有的人就相当于“黑天鹅事件”。除此之外,人们发现网站的点击量、文件的下载量、城市的规模、地震的规模、战争的规模、不同人的好友数量等都服从幂律分布,这是规模法则的另一种体现。前文提到的齐普夫定律也是幂律分布的一种表现形式。关于这一主题还有非常多值得讨论的内容,本书限于篇幅暂且不涉及[6]。
1997年,杰弗里·韦斯特(Geoffrey West)、詹姆斯·布朗(James Brown)和布莱恩·恩奎斯特(Brain Enquist)等人在《科学》上发表文章,提出了著名的WBE模型,为克莱伯定律给出了令人信服的解释。克莱伯定律这一话题再一次被提起,成为生物学界关注的焦点。之后,韦斯特等人开始大刀阔斧地进行更深入、更广泛的研究。首先,他们通过收集更广泛的生物学数据,在更大的尺度范围内验证了克莱伯定律。小到细胞内部的线粒体,大到蓝鲸,克莱伯定律在20多个数量级的大尺度范围内都适用。其次,大量的生物学特征,包括寿命、心跳频率等因素与规模大小的依赖关系都可以从克莱伯定律中推导出来。更进一步,韦斯特等人从克莱伯定律出发推导出了生物体普适的生长曲线。从此,克莱伯定律成为了生物学中少有的定量性的基础规律。
到了2009年,韦斯特联合贝当古等人又将规模分析方法引入了城市系统的研究之中,并提出了社会经济系统中的异速规模法则。这些规模法则可以分为三种:基础设施与城市规模的亚线性规模法则(幂指数小于1);个人、家庭相关变量的线性规模法则;以及社会经济活动的超线性规模法则(幂指数大于1)。与生物体中的克莱伯定律不同的是,城市的新陈代谢率,即人类的社会经济活动,与城市规模之间存在超线性规模法则——城市规模越大,发展节奏就越快,进而导致超指数增长——在有限的时间内城市规模会增长到无穷大。然而,有限的资源必然会阻止无限的生长,于是城市通过科技创新重置生长过程。即使经历了动力学重置,城市发展的总体进程仍然会不断加速,韦斯特和贝当古的理论预言城市最终会迈向奇点。
我于2010年发表文章,系统性地探讨了国家中的规模法则:包括国家宏观广延量(满足可加和性质的变量,如总人口、GDP等)的规模法则和强度量(不可加和的变量,如生育率、人均GDP等)的规模法则。我们发现,对于同样的变量,国家和城市的规模法则幂指数存在明显的不同。例如城市的GDP与人口之间存在超线性规模法则,而国家的GDP与人口则为近似线性关系。这说明城市的高度聚集效应是超线性规模法则产生的原因。
更进一步,我与合作者还研究了互联网社区中的规模法则,发现互联网社区与城市存在一定的相似性,社区的各类活动与用户数之间存在明显的超线性规模法则。这进一步说明聚集效应是导致各种规模法则的主要原因。我们还对百度贴吧中的注意力流进行了分析,发现了广义克莱伯定律,且幂指数大小可以作为贴吧用户黏性的衡量指标。本书的后续章节会对这部分内容进行详细讨论。
大概在2010年,我加入圣塔菲研究所的韦斯特研究小组,并与马库斯·哈密尔顿(Marcus Hamilton)及克里斯·肯普斯(Chris Kempes)等人合作研究公司的规模法则。我们对比了美国近3万家和中国3000多家上市公司的规模法则,并试图将其与公司的生长行为联系起来。目前这一研究已经得到了一些初步结果,并仍在进行之中。
注释
[1] NASA曾经拍摄了一个视频向我们展示神奇的规模缩放之旅。
[2] 有关分形的进一步探讨,可参见曼德尔布罗著的《大自然的分形几何学》。
[3] 按照这个分形雪花的数学定义,它边缘上的折线会在更小的尺度上无穷延伸下去。所以,当放大一段曲线的时候,我们就能看到曲线上更为细节的折线结构。但由于印刷精度有限,因此图2.5无法展现更为细节的结构。
[4] 1英寸为2.54厘米。——编者注
[5] 有关规模分析的历史,可以参考达西·汤普森著的《生长和形态》以及杰弗里·韦斯特著的《规模》。
[6] 更多有关幂律分布的探讨,可以参考马克·纽曼(Mark Newmann)的经典文章:“Power laws, Pareto distributions and Zipf’s law”以及塔勒布著的通俗读物《黑天鹅》。
活动预告


集智学园VIP双十一限时特惠,加入即可解锁集智所有资源,并有机会获得《规模法则》赠书和其他周边礼品!详情请见:《一次解锁集智所有资源,双十一集智学园VIP限时优惠来啦!》
推荐阅读
1. 深度解读2021年诺贝尔物理学奖——平衡混沌与秩序的复杂2. 21世纪为什么需要复杂科学?3. 张江新书发布!《规模法则——探索从细胞到城市的普适规律》4. 吕琳媛:施必适其量,用必思其器 | 《规模法则》推荐序5. 复杂物理学是可能的吗?|《规模法则》新书试读6. 张江:第三代人工智能技术基础——从可微分编程到因果推理 | 集智学园全新课程7. 一次解锁集智所有资源,双十一集智学园VIP限时优惠来啦!8. 加入集智,一起复杂!
点击“阅读原文”,报名读书会





 ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง
ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง





