极市导读
本文介绍了深度神经网络量化的基本概念和方法简介。深度神经网络越来越多地用在边缘计算中,而边缘计算的设备通常算力较低,且会受到内存和功耗的限制。而且,有必要减少从云端把模型下载到移动设备上所需要的通讯频带和网络连接的资源。因此,需要一些技术来优化模型的大小,以实现更快的推理和更低的功耗。 >>加入极市CV技术交流群,走在计算机视觉的最前沿
本文目录
1 深度神经网络量化白皮书
(来自 Google)
1.1 模型量化的实际意义
1.2 均匀仿射量化
1.3 均匀对称量化
1.4 随机量化
1.5 伪量化
1.6 决定量化参数
1.7 量化粒度
1.8 后训练量化
1.9 量化感知训练
太长不看版
本文介绍了深度神经网络量化的基本概念和方法简介。深度神经网络越来越多地用在边缘计算中,而边缘计算的设备通常算力较低,且会受到内存和功耗的限制。而且,有必要减少从云端把模型下载到移动设备上所需要的通讯频带和网络连接的资源。因此,需要一些技术来优化模型的大小,以实现更快的推理和更低的功耗。前几个小节介绍的是线性量化操作,后面两个小节介绍的是主流的两种量化技巧,即后训练量化和量化感知训练。
1 深度神经网络量化白皮书
论文名称:Quantizing Deep Convolutional Networks for Efficient Inference: A Whitepaper
论文地址:
https//arxiv.org/pdf/1806.08342.pdf
1.1 模型量化的实际意义
深度神经网络越来越多地用在边缘计算中,而边缘计算的设备通常算力较低,且会受到内存和功耗的限制。而且,有必要减少从云端把模型下载到移动设备上所需要的通讯频带和网络连接的资源。因此,需要一些技术来优化模型的大小,以实现更快的推理和更低的功耗。
模型量化的实际意义有:
- 适用于一系列的模型和使用场景:无需复杂的模型设计,任意的浮点数模型,都可以快速量化成为定点数模型,基本没有精度损失,且无需重新训练。许多的 hardware platforms 和 libraries 都支持。
- 模型尺寸更小 (weight quantization):8-bit 量化时,模型缩小4倍,下载时间都快了。
- 减少存储推理激活值所需的 working memory 和 cache (activation quantization):推理时的中间计算结果通常存储在 cache 里,以便后面层的重用,降低这些数据的精度可以减少所需的 working memory 和 cache。
- 更快的计算:大多数处理器允许更快的处理 8-bit 数据。
- 更低的功耗:移动 8-bit 数据所需的功耗要远小于移动 32-bit 数据,在许多架构数据搬运决定功耗。因此,量化会对功耗有影响。
1.2 均匀仿射量化
给定一个范围在 之内的浮点数,需要将其量化到 的范围,其中如果是 8-bit 的量化则有 。
下面定义 2 个参数: Scale 和 Zero-Point 。
Scale 指定了量化后的数值,每前进一次,浮点数增加的数值。
Zero-Point 是一个量化后的整数,指示了浮点数的 0 被量化到了哪里。
对于数据分布在一侧的情况, 会被外扩,以包含数值0,比如浮点数的分布在 ,它会被先外扩到 ,然后再量化。请注意,在极端单边分布的情况下,这可能会导致精度损失。
一旦 Scale 和 Zero-Point 确定之后,量化的过程如下::
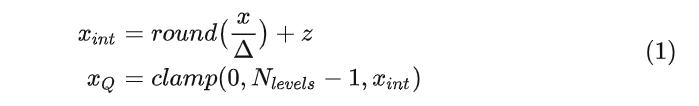
其中, 是量化之前的浮点数, 是量化之后的整数,且有:
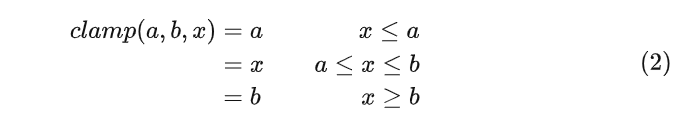
我们也可以发现,当 时, ,即: 当浮点数的0时,被量化到了 Zero-Point。
解量化 (de-quantization) 的操作是:

虽然均匀仿射量化允许以 8-bit 的精度存储 weight 和 activation,但由于 Zero-Point 的原因,还有一个额外的成本。考虑 weight 和 activation 之间的 2D 卷积:
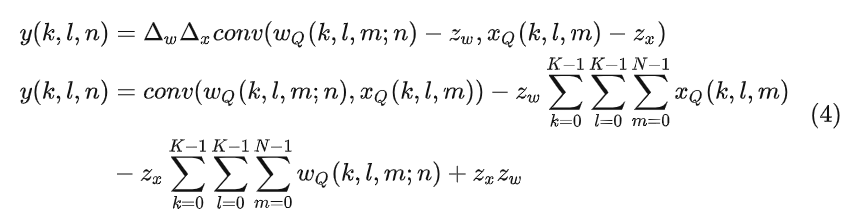
1.3 均匀对称量化
均匀对称量化是指 Zero-Point 强制为0,即:浮点数的0时,量化结果为0。对称仿射量化的过程如下:
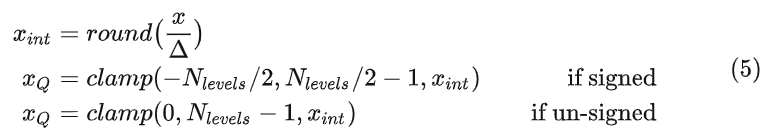
为了更快的 SIMD 实现,可以进一步限制权重的范围。在这种情况下,clamp 可以修改为:
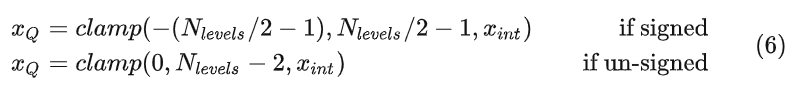
这里可以进一步参考[1]。
解量化的操作是

1.4 随机量化
随机量化时,会在量化过程中添加一个加性噪声,然后进行舍入。随机量化的过程如下式所示:
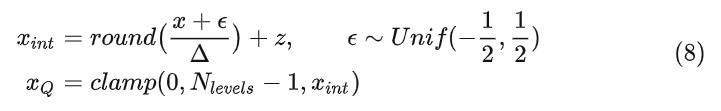
解量化的操作如式3所示。不考虑随机量化进行推理,因为大多数推理硬件不支持。
1.5 伪量化
伪量化是量化感知训练 (Quantization-aware training) 中的常用技术。在量化感知训练中,一般使用模拟量化 (伪量化) 的操作,其包含一个量化器和一个解量化器:
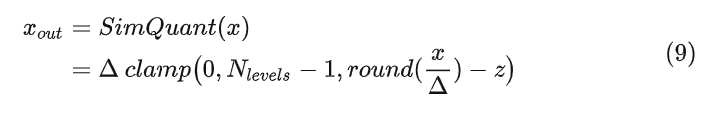
因为量化过程存在四舍五入 操作,因此反向传播通过它时计算得到的导数几乎处处为零,因此需要在反向传播中对量化器进行建模,也就是通过使用下面的 操作,如图1所示。
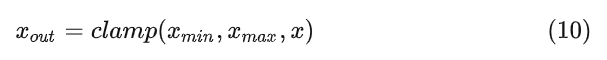
反向传播通过 Straight Through Estimator (STE)[2] 方法进行建模:
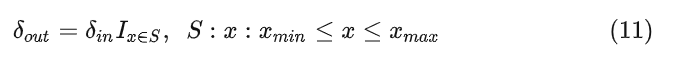
式中, 是损失函数 对输出的导数。
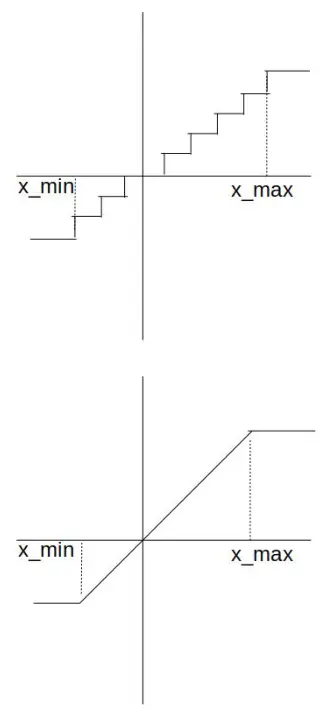 图1:(上) 导数处处为0的 round 操作。(下) 可以求导的 clamp 操作
图1:(上) 导数处处为0的 round 操作。(下) 可以求导的 clamp 操作
1.6 决定量化参数
量化器参数可以使用几个标准来确定。例如,TensorRT[3]最小化了原始分布和量化分布之间的KL散度,以确定步长。本文采用了更简单的方法:
对于 weights:使用实际值和最大值来确定量化器 Scale 参数。
对于 activations:使用 mini-batch 中的最小值和最大值的移动平均值来确定量化器 Scale 参数。
1.7 量化粒度
Per-Layer Quantization:为整个的 weight tensor 设置一个 Scale 参数和一个 Zero-Point 参数。
Per-Channel Quantization:为每个卷积核设置一个 Scale 参数和一个 Zero-Point 参数。
weight tensor 是 4 维,包含了 个卷积核,每个卷积核负责产生一个输出特征图。Per-Channel Quantization 对每个卷积核都有不同的 Scale 和 Zero-Point 参数。另外,不考虑 activation 的 Per-Channel Quantization,因为这会使核心的内积计算变得复杂。
1.8 后训练量化
后训练量化 (Post Training Quantization) 通过压缩 weights 和 activations 来实现更快的推理以及减小模型的大小,且无需重新训练模型。后训练量化允许在有限的数据下进行量化。
只量化权重
一种简单的方法是只将浮点数的权重量化到 8-bit。这种方法只是将 FP32 模型的 weights 降低到 8-bits,而不量化 activations。由于只有权重被量化,这可以在没有任何验证数据的情况下完成。如果只是希望量化模型传输和存储的大小,而不考虑到以 FP32 来执行推理的成本,这种设置会很有用。
量化权重和激活值
可以通过计算要量化的所有量的量化器参数,可以将浮点模型量化为8位精度。由于激活需要量化,因此需要一个校准集,并且需要计算激活值的动态范围。通常,大约 100 个 mini-batch 就足以估计要收敛的激活值的范围。本文通过实验发现,Per-layer 的 Weight Quantization 导致较大的精度下降的主要原因是 Batch Normalization,这导致单层卷积核动态范围的极端变化。Per-channel 的 weight quantization 可以回避这个问题,这使得 Per-channel 量化的精度与 BN 的 scaling factor 无关。
Activation Quantization 仍然使用 Per-layer 的对称量化策略。
1.9 量化感知训练
量化感知训练 (Quantization aware training) 在训练期间量化,可以提供比 Post Training Quantization 方案更高的精度。本文使用模拟量化操作对权重和激活的影响进行建模。对于反向传播,本文使用直通估计器 (Straight Through Estimator) 来模拟量化。本文对前向传播和反向传播使用模拟量化,并维护一套 FP32 的权重,并且使用梯度更新来优化它们。这可以确保较小的梯度更新直接作用在 weight 上面。更新之后的权重会接着再用于下面的前向传播和反向传播。
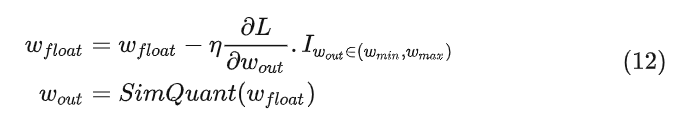
式中, 是模拟量化过程的输出, 是模拟量化过程的输入。
下图2是 Quantization aware training 的计算图。
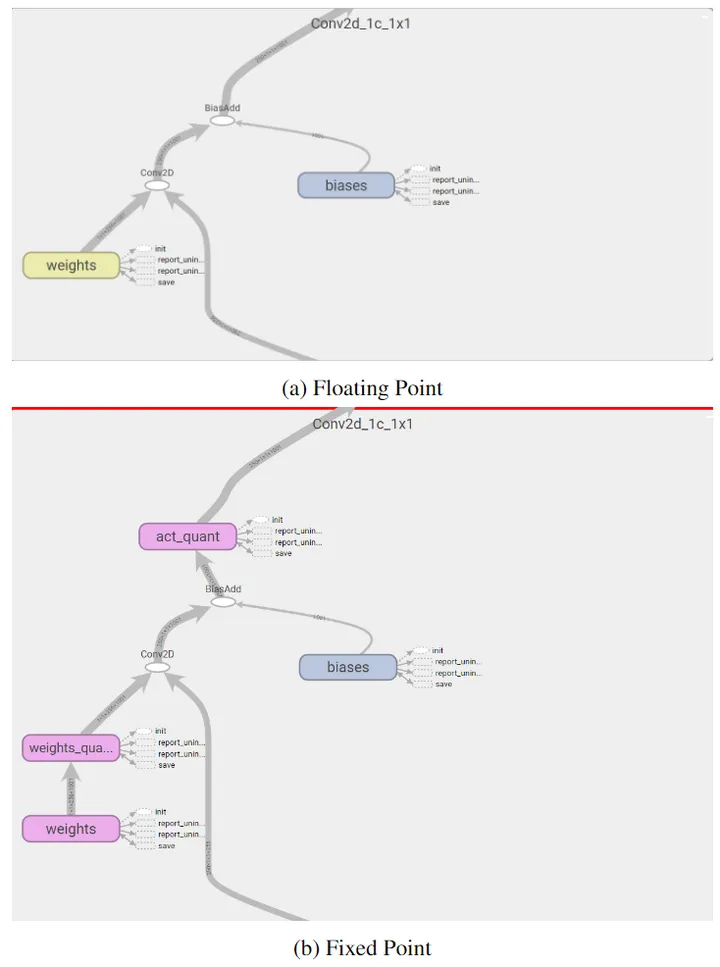 图2:Quantization aware training 计算图
图2:Quantization aware training 计算图
作者还介绍了 Batch Normalization 的量化方法。BN 由以下方程定义:
训练:
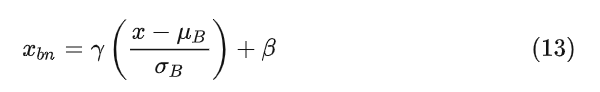
推理:
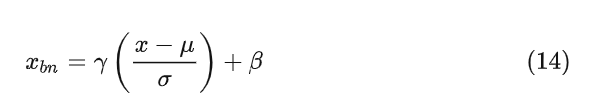
其中, 和 是 mini-batch 的均值和标准差, 和 是 mini-batch 的均值和标准差,并在训练期间计算为批量统计的移动平均值。
对于推理,作者将 Batch Normalization 改为由下2式定义的权重。因此,在推理时没有明确的 Batch Normalization。
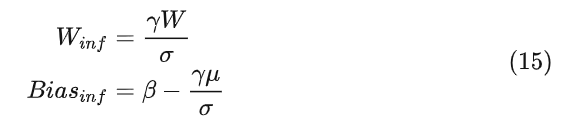
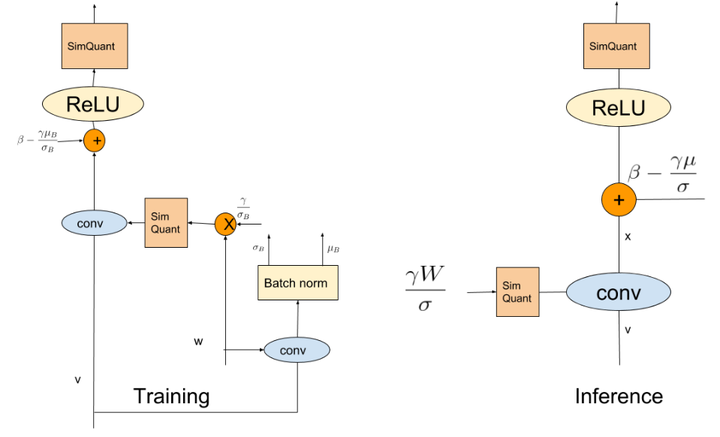 图3:Batch Normalization 的训练和推理示意图
图3:Batch Normalization 的训练和推理示意图
Batch Normalization 的训练和推理示意图如上图3所示。
在 training 时: 是上一层的 INT8 输出,经过 SimQuant 伪量化之后的卷积的作用计算 INT8 卷积的结果。其中,卷积的参数已经乘以了 。计算得到的结果再加上 得到等效的 输出,最后经过 SimQuant 伪量化得到该层的计算结果。其中, 是使用浮点数权重计算得到的。
在 inference 时: 是上一层的 INT8 输出,经过 SimQuant 伪量化之后的卷积的作用计算 INT8 卷积的结果。其中,卷积的参数已经乘以了 。计算得到的结果再加上 得到等效的 输出,最后经过 SimQuant 伪量化得到该层的计算结果。
参考
1.Quantization and Training of Neural Networks for Efficient Integer-Arithmetic-Only Inference
2.BinaryConnect: Training Deep Neural Networks with binary weights during propagations
3.8-bit Inference with TensorRT





 ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง
ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง





