你的公司有没有偏离规模法则？中美对比、企业评估与生长预测

导语

复杂系统，从生命系统到繁复的生态系统，再到互联网社区、城市乃至企业结构，表面看似乎毫无联系，属于各自独立的学科领域，但深入挖掘下去，就能发现一系列统一的规律横贯其间。其中“规模法则”以其简洁而深远的影响力脱颖而出，揭示了复杂系统中宏观变量如何随着系统规模的扩大而变化。这些简单数量关系背后隐含着对复杂系统普遍适用的基本原理的深刻理解。
在集智俱乐部「复杂系统管理学读书会」中，北京师范大学系统科学学院教授、集智俱乐部创始人张江老师以企业这一开放的复杂适应系统为例，探讨了企业的规模法则与生长规律。长期以来，企业的增长被认为充满不确定性，受政治、经济和营商环境等因素的多重影响。但最新研究通过规模法则和财务平衡的基本原理，从数学角度推导出了一个确定性的企业生长方程。这一发现不仅解决了理论界对于吉布莱特定律长期的争论，还预测了一种前所未有的现象——“奇点”。企业生长的奇点实际上是一种临界规模，它设定了企业生长的上限，没有任何企业能够在长期超越这一“天花板”。更为引人注目的是，这一理论揭示了奇点与市场中债务和总资产的规模法则之间的紧密联系。
研究领域：复杂系统，规模法则，企业生长，奇点张江 | 讲者管桑田 | 整理
目录

0. 引言

1. 企业研究

2. 企业中的统计规律

– 齐夫定律

– 规模法则

– 公司规模法则及其偏离

3. 公司的生长

– Gibrat 假说：企业生长是一个随机过程

– Stanley 的推广：企业的统计物理学

– 从规模法则得到生长方程

4. 奇点

5. 结语

0. 引言

在艾萨克·阿西莫夫笔下的《基地》系列中，银河帝国的恢弘图景令人印象深刻：疆域横亘整个银河系，雄踞2500万颗定居行星，首都有着超过400亿人定居。这个盛极一时、风头无两的宇宙帝国，正是通过心理史学 (Psychohistory)——一种融合心理学、社会学、经济学的万物统一理论——实现对大规模人类群体行为的精确预测，并因此达到了其辉煌的顶峰。但这是科幻！

《基地》系列科幻小说

而复杂科学作为一个新兴学科，正尝试着追寻如同心理史学一般的万物理论，这是现实！复杂科学作为一种新的万物理论，其渊源与物理学的本源思想有着密不可分的关系。

第谷，开普勒与牛顿

同是探寻事物运行普遍规律的学科，从第谷的星表收集到开普勒的行星运动定律，再到牛顿的力学理论，物理学自底而上探索物性的研究思想，可以被类比作一种对“硬件”的研究过程。相对的，复杂科学可以被类比为一门研究“软件”的学科。复杂科学将研究的方法从还原论 (reductionism) 转向了整体论 (holism)，将研究重点从物质的性质转向了由物质构成的复杂系统的整体结构，试图揭示这些结构中隐藏的普遍规律。作为复杂科学的“开普勒定律”，规模法则 (scaling laws) 最早由美国学者Geoffrey West进行大规模跨学科的系统性研究，描述了当对一个复杂系统进行规模缩放时，系统内其他变量展现出的对规模大小的幂律依赖关系。规模法则的适用范围极为广泛，从生物学到城市规划，都可以找到它的身影。
以生物学中的克莱伯定律 (Kleiber’s law) 为例，该定律的普适范围惊人地囊括了跨越27个数量级的各种生物体，揭示了生物体代谢率与体重之间存在的幂律关系，精准预测了数十种哺乳类动物的生长规律。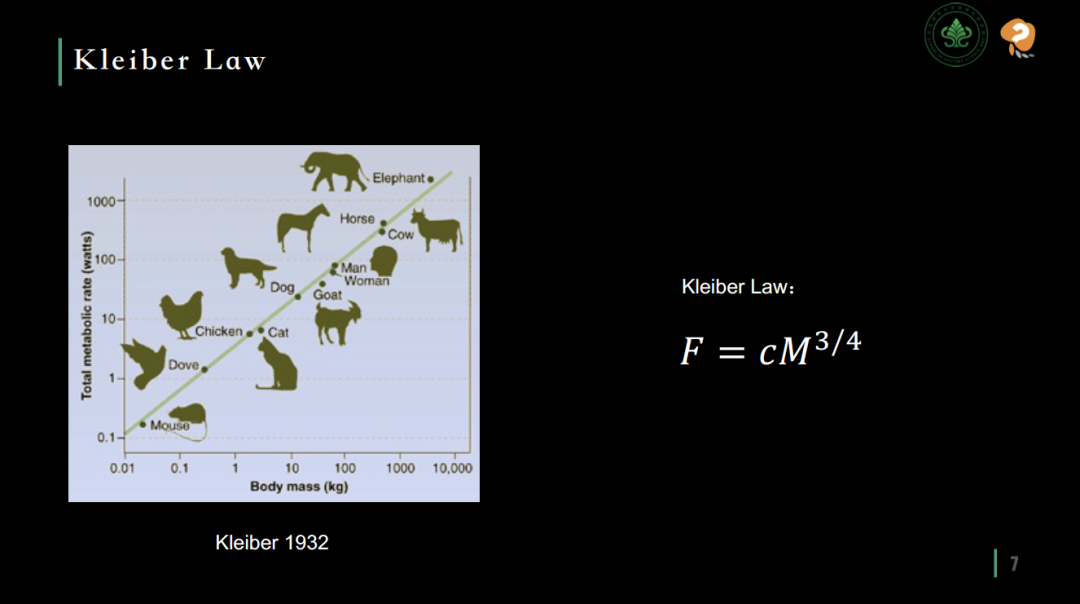

克莱伯定律

规模法则同样适用于城市规划领域。将规模换做人口，“代谢率”类比为城市的国内生产总值 (GDP) 后，规模法则将可用于刻画城市的生长过程，从而理解和预测城市的发展趋势，这也同时解释了为何“大城市更容易集聚机会”。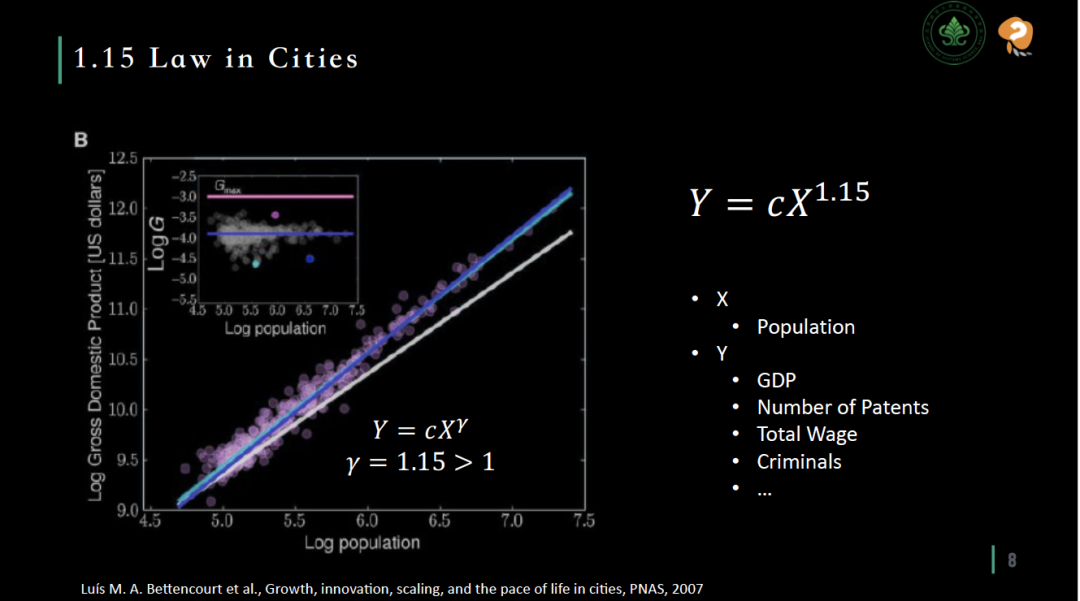

城市的规模法则

企业的增长充满了不确定性和随机性，传统方法对企业增长的预测效果并不理想。本次讲座，张江老师带我们穿越企业增长的不确定性 (stochastic)，借由规模法则探究企业生长的确定性 (deterministic)，通过分析企业的各种变量对员工数量和总资产 (total asset) 这两类关键规模变量的规模法则，得以更深入地理解企业规模生长 (growth) 的内在规律，进而为企业的可持续发展提供新的视角和策略。

1. 企业研究

企业作为现代经济的核心组成部分，其特征和运作机制一直是商业和经济学研究的重点。为了更深入地理解企业，我们可以从几个关键视角进行观察和分析。
首先，从组织结构的角度来看，企业可以被视为一种人的集合体。这种视角强调了不同组织架构对企业行为和文化的影响。例如，一个层级清晰的组织可能在决策效率上有优势，而一个扁平化的组织可能更能激发员工的创新和参与感。然而，这种视角的挑战在于组织文化和人际互动的复杂性难以量化，使得其对企业成功的影响难以用数字精确描述。

从组织的视角分析公司

Lera SC, Sornette D (2019) A theory of discrete hierarchies as optimal cost-adjusted productivity organisations. PLoS ONE 14(4): e0214911. https://doi.org/10.1371/journal.pone.0214911
第二个视角是通过财务和货币流 (Money Flow) 来考察企业。这种方法利用财务数据和会计技术，将企业的运营活动量化为数值，从而精确描述企业的健康状况和发展趋势。例如，通过分析利润表、资产负债 (Liabilities) 表和现金流量表，可以对企业的盈利能力、资产负债状况和现金流动性进行深入分析。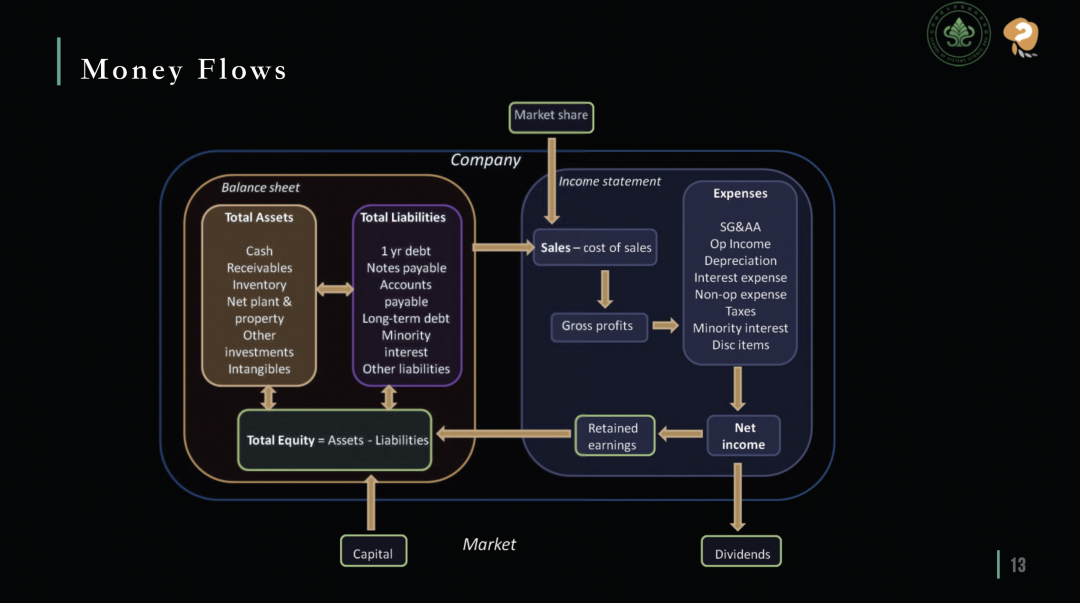

从货币流的角度考察公司

第三个视角关注的是外部环境对企业的影响。宏观经济指标、地缘政治局势、国际贸易环境等因素都会对企业产生重大影响。例如，全球经济衰退可能导致消费者需求下降，而政治稳定性的提高可能为企业提供更有利的经营环境。

从外部环境出发观察公司

第四个视角则着眼于企业的网络关系。通过分析企业的供应链网络、股权结构和合作伙伴关系，我们可以评估企业的市场地位和运营的可靠性。例如，一个拥有强大且稳定的供应链网络的企业，可能比依赖于少数供应商的企业在市场中更具竞争力和抗风险能力。

从网络的视角理解公司

然而，尽管上述每种视角都为理解企业的运作提供了有价值的洞见，但大多数研究仍然集中在单个企业层面，缺乏对企业群体整体特性的考量。因此，这些研究得出的规律往往只适用于特定情境，而不具有普遍适用性。当研究的视角不再执着于传统的盈利预测，而转向关注企业生长时，更富确定性的生长规律便开始浮现。

2. 企业中的统计规律

在本次讲座中，张老师展示了一项涉及大量中国和美国上市公司的研究。这项研究使用的数据集非常庞大，包含了众多上市公司的详细财务信息。倘若仅尝试将这些公司的总资金量与时间进行直接对比并将其可视化后，在所得的图表上两者之间似乎没有明显的规律。这种初步的观察可能让人觉得，企业的发展似乎是一种随机的、无法预测的过程。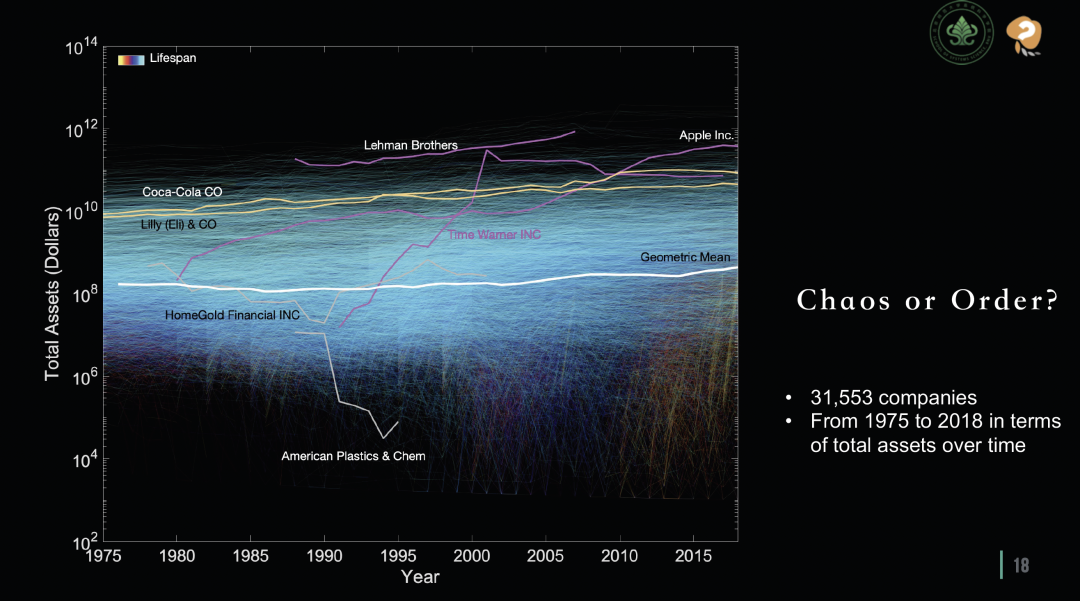

混沌抑或是有序？

然而，张老师的研究聚焦于企业的规模，通过规模法则提供一种全新的视角，用规模这把“尺子”来理解和解释企业群体的发展模式，挖掘普适的规律和趋势。

2.1 齐夫定律

齐夫定律 (Zipf’s law)，由统计学家George Kingsley Zipf提出，最初是在研究自然语言文本时发现的一种现象。他观察到，在一篇文章中，词语的出现频率是不均等的。当把文中的词语按照出现频率从高到低排序，就可以观察到一个有趣的规律：最常出现的词汇数量远超过其他的。这种词频分布特性，后来被广泛地认为适用于许多自然和社会现象。
齐夫定律同样适用于对企业生长的分析。首先，将企业按照雇员数量从多到少排列在横坐标上，然后用纵坐标表示每个企业的雇员数量。为了更清晰地展示数据，横纵坐标都取了对数，于是就得到了两组反映中国和美国市场就业异质性 (heterogeneity) 的曲线。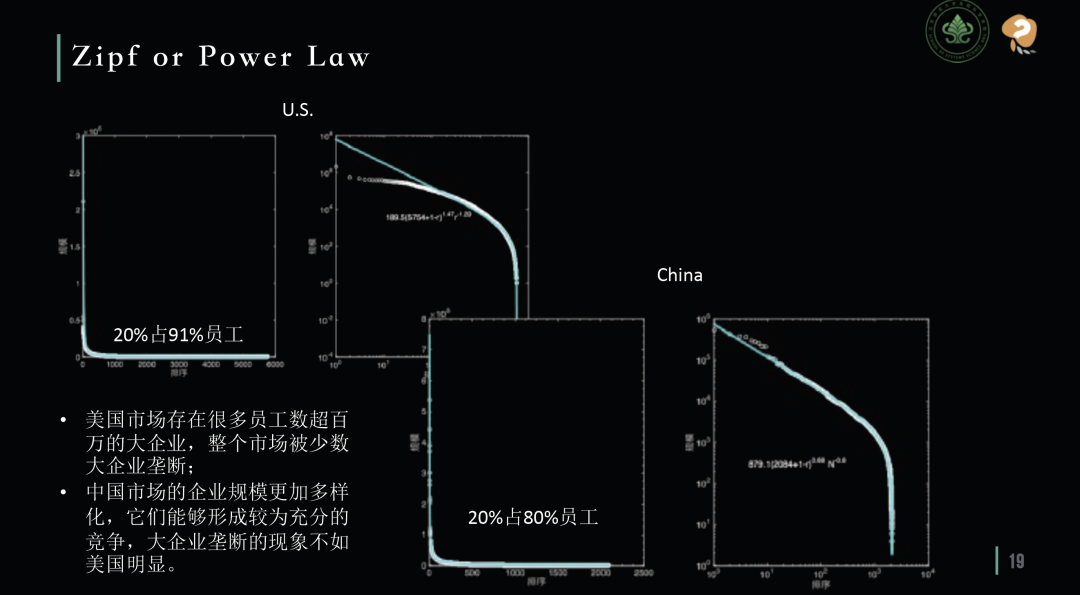

应用齐夫定律分析就业市场

这些曲线揭示了一个关键的社会经济现象：就业市场的不平等程度。斜率越陡的曲线意味着市场中的不平等更加显著，即少数大企业控制了大量的雇员资源，而大多数小企业只能分到很少的雇员。从这些图表中不难看出，在美国市场，前20%的大企业拥有91%的员工，这表明美国的大企业垄断现象更为明显。相比之下，中国市场遵循着更接近于二八准则的分布，即前20%的企业拥有大约80%的雇员。
这种基于齐夫定律的分析，仅仅利用员工数量这一单一变量，就能揭示出市场中就业分布的不平等情况。这正是利用复杂系统的统计方法来分析数据的优势所在，它不仅提供了一个简洁的工具来理解复杂的市场动态，而且还有助于洞察企业群体和整个经济体系中的基本趋势和结构特征。

2.2 规模法则

在深入研究企业发展过程中，张江教授团队运用了规模法则来探索营业额的统计规律。针对某一特定年份，以企业的雇员数量作为横轴，公司的总销售额作为纵轴，并对这两个变量进行对数处理，便可以得到一张反映中国和美国上市企业“员工数-总销售额”关系的散点图。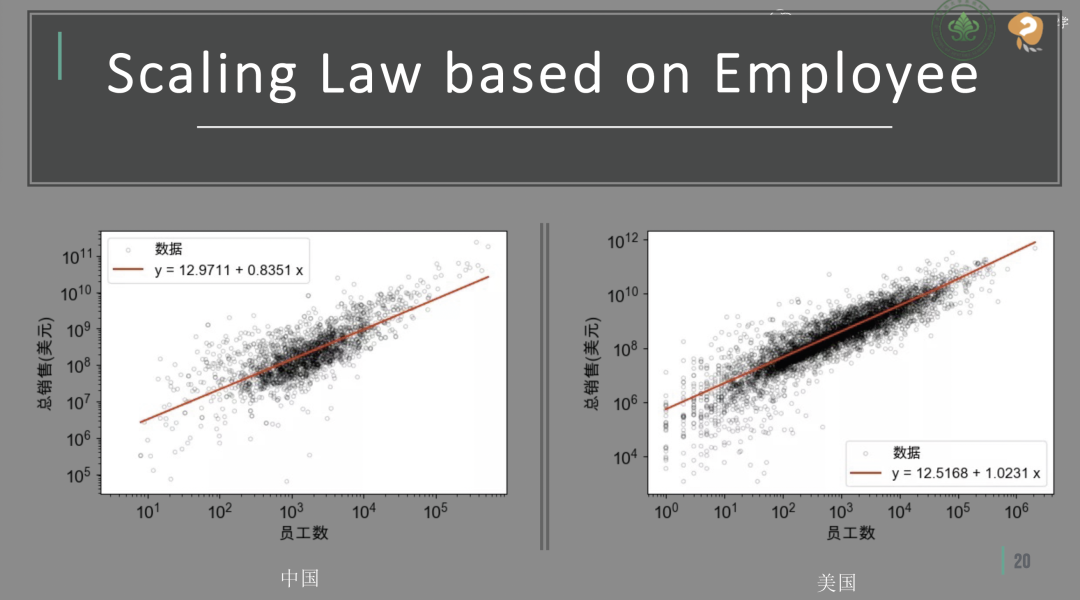

基于雇员数目的规模法则

将这些数据用直线拟合后，就可以得到两条展示中美企业规模法则的直线。这些拟合直线的斜率和截距为研究提供了两个重要的分析维度：

• 斜率，经济学中称其为弹性系数 (elastic coefficient)，这里称之为规模法则的幂指数。分析后在图中可见，中国企业的幂指数为0.8351，数值小于1，这表示中国企业随着员工数量的增加，营业额的增长速度将会放缓，也即大公司的人均销售额相对较低。而美国的幂指数大于1，意味着其企业营业额增长速度随员工数量增加而加速，大企业与小企业在销售业绩上差异不显著。
• 截距，由于坐标轴采用对数表示，截距反映的是企业仅有一名员工时的销售额。在这个维度上，中国企业的销售额数值高于美国，表明在单个员工的销售能力上，中国员工的表现更为强劲。然而，随着企业规模的扩大，中国企业的人均销售额呈现下降趋势。

此外，规模法则也揭示了企业老化的统计规律。不将研究限定在某一特定年份，而是将所有成立一年的企业纳入分析后，便得到了一张揭示初创企业营业额规模特征的散点图。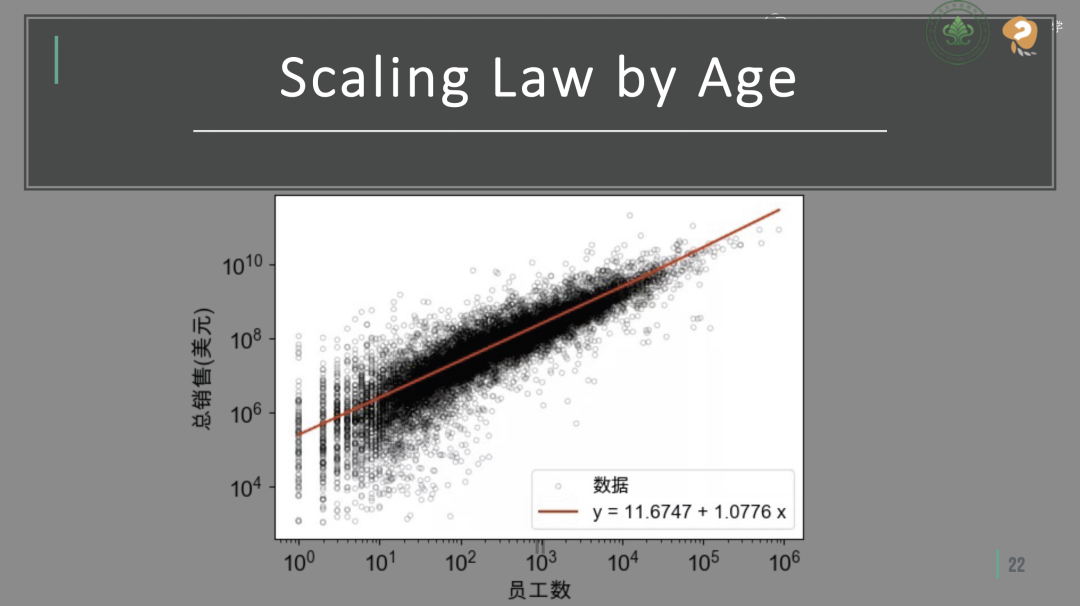

企业存续时长的规模法则

通过同样的方法，分别统计成立不同年份的企业，并分析多个发展指标的规模法则后，就可以观察到各指标随着企业成立时间的变化趋势。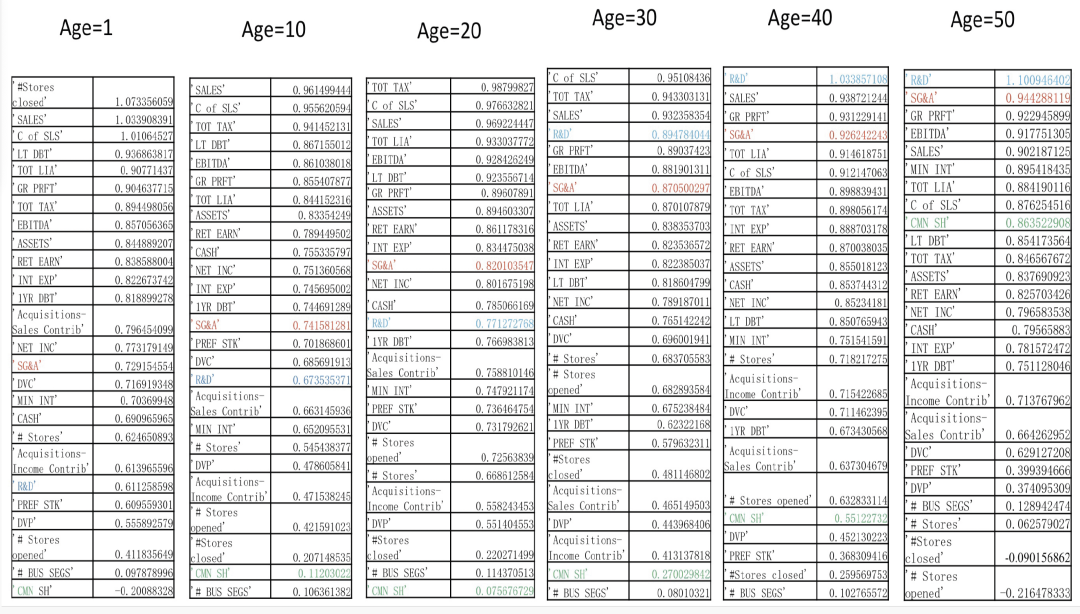

企业的老化

先前所关注的企业销售额 (SALES)，其表中数值在0.902~1.034之间波动，变化幅度不大。老化相对明显的是运营成本 (SG&A) 这一指标，在企业1岁时它的数值是0.729，而到了最右侧在企业50岁时，该数值已经接近于1，同样变化明显的还有研发成本 (R&D) 等指标。从中可以发现，随着企业的老化，更大的企业规模带来的将会是更多的成本，营收增长的规模效应将在企业的老化过程中弱化。
规模法则为比较不同企业提供了一个全新的评估维度。在传统的企业投资分析中，人们通常会通过计算企业的财务比例 (Ratio) 指标来评估其经营状况，例如利润率、资产负债率 (asset liability ratio) 等。然而，当意识到企业中存在规模法则时，就会发现这些基于比例的指标并不总是能准确反映企业的实际情况。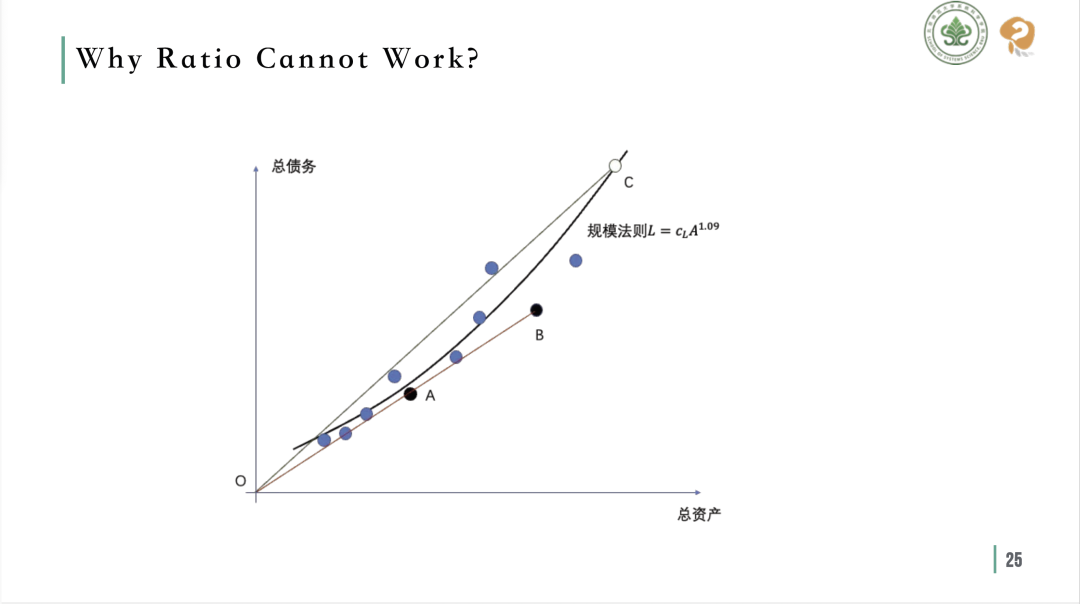

比例指标已不再适用

2.3 公司规模法则及其偏离

以企业的总资产和负债为例，张老师团队和合作者通过分析不同规模企业的总资产，发现了资产和负债之间存在1.09次幂的关系。这个发现意味着，随着企业总资产的增加，其资产负债率呈现出超线性增长的趋势。因此可以得出结论：企业的资产和负债之间并不是简单的线性关系。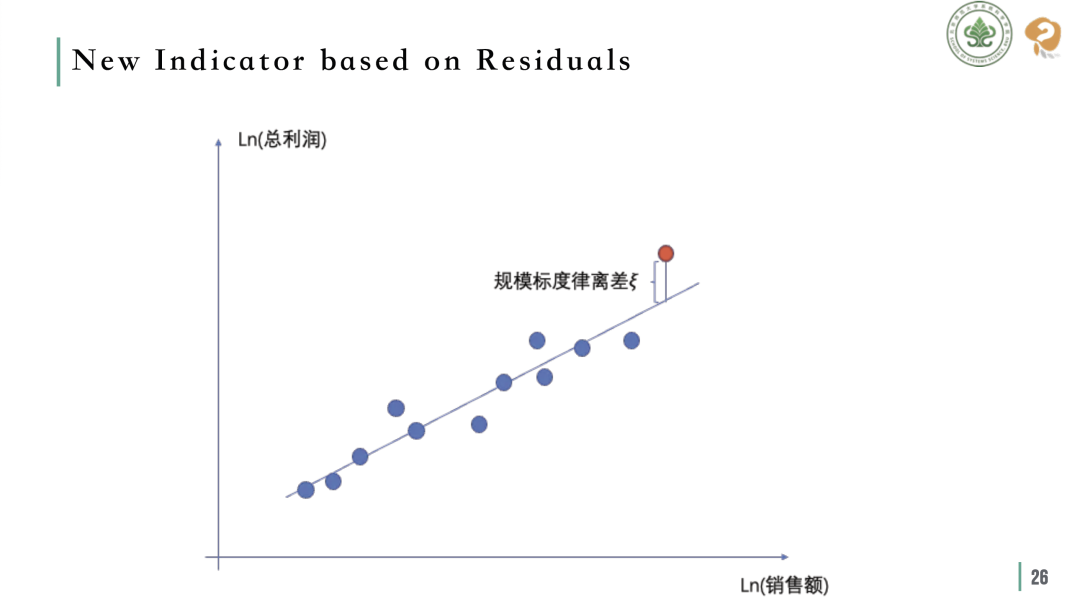

基于离差(Deviation)的新评估指标

Xu J, Chen X, Wen L, Zhang J (2023) Company scaling and its deviations: New indicators for enterprise evaluation and bankruptcy prediction. PLoS ONE 18(10): e0287105. https://doi.org/10.1371/journal.pone.0287105
进一步地，将负债视作企业发展的非积极指标为前提，在比较两家公司B和C时，如果发现B公司的资产负债率低于平均水平 (即位于幂律曲线的下方)，而C公司的资产负债率等于平均水平，则可以推断B公司在负债管理上优于C公司。基于这种认识，张老师团队和合作者提出了一种新的评估标准——离差指标 (deviation indicators)。这个指标通过分析公司的表现与平均曲线的偏离程度来评估其优劣。例如，对于一些积极的经营指标，公司在平均曲线之上的偏离程度越高，说明其表现越好；反之亦然。
为了验证离差指标的有效性，研究中对2008年美国上市企业的总毛利和总销售额进行了基于规模法则的离差指标分析。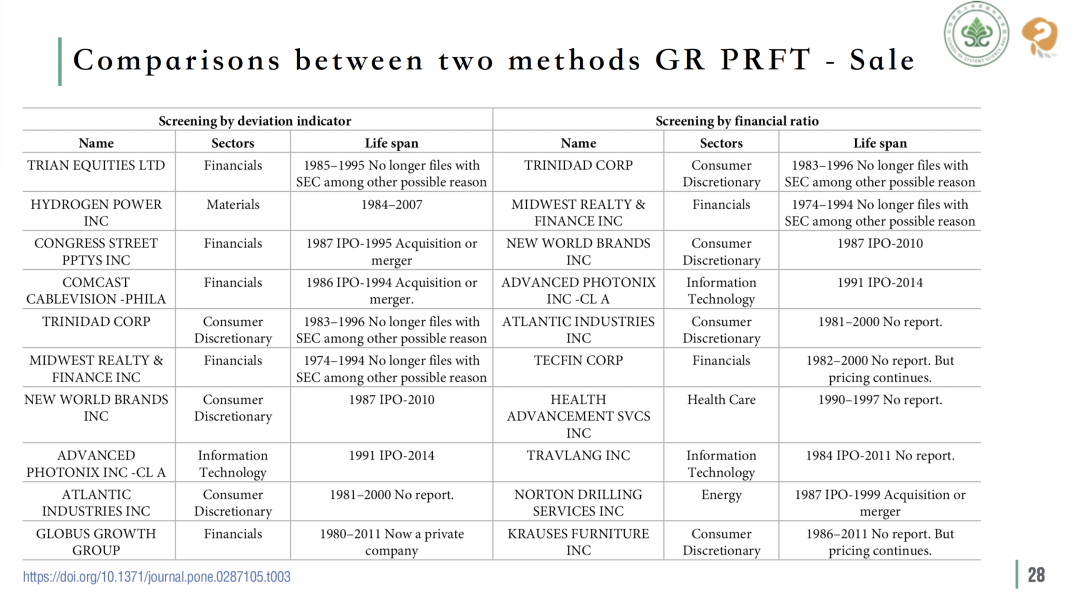

对比离差指标 (左)与比例指标 (右)对美国企业的优劣筛选结果

通过与传统的比例指标进行对比，从表中可以得知，比例指标筛选出的最优公司在离差指标排序中排名第五，表明两种指标之间的差异不会过大。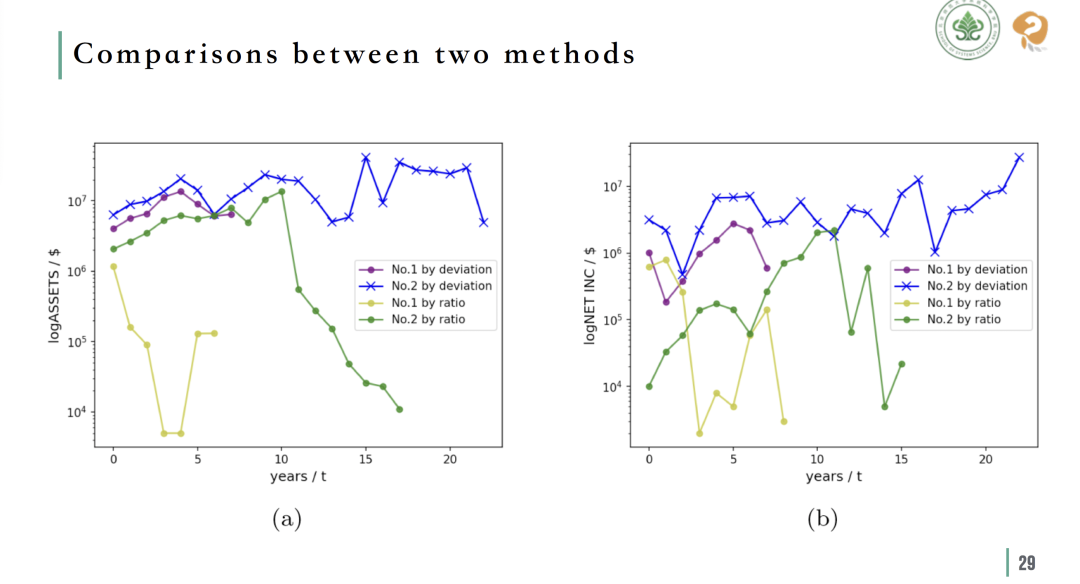

两种指标所选top2公司的未来发展对比

然而，在跟踪分析两种指标筛选出的前两名公司的后续发展情况时，可以发现离差指标选出的公司在毛利和净收入方面表现更佳，发展也更加稳定。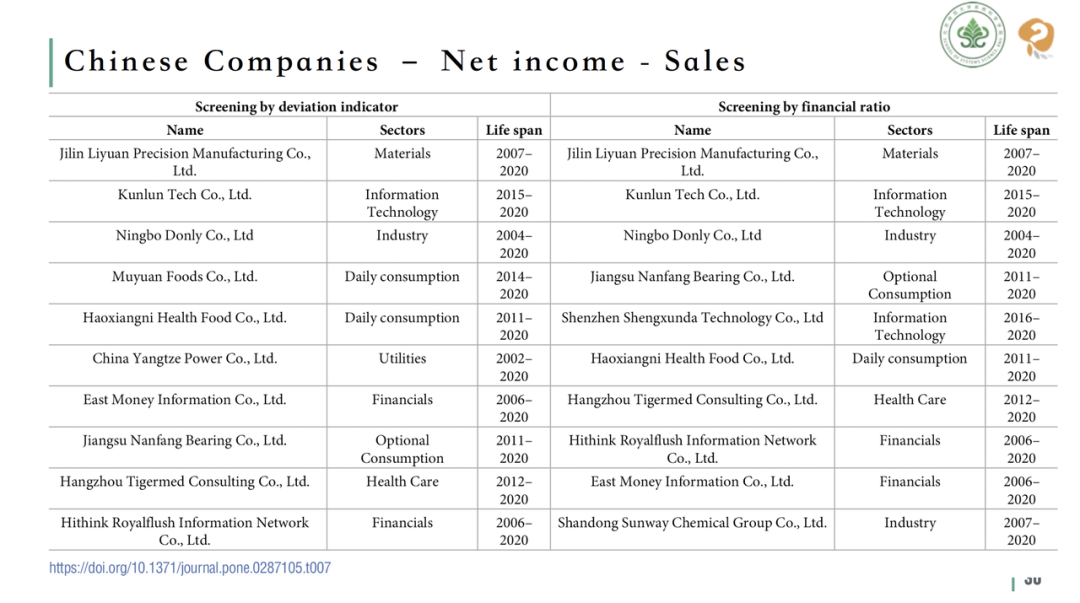
对比离差指标 (左)与比例指标 (右)对中国企业的优劣筛选结果
对中国市场的同样分析显示，虽然前三名公司在两种指标下保持一致，但第四名开始出现明显差异。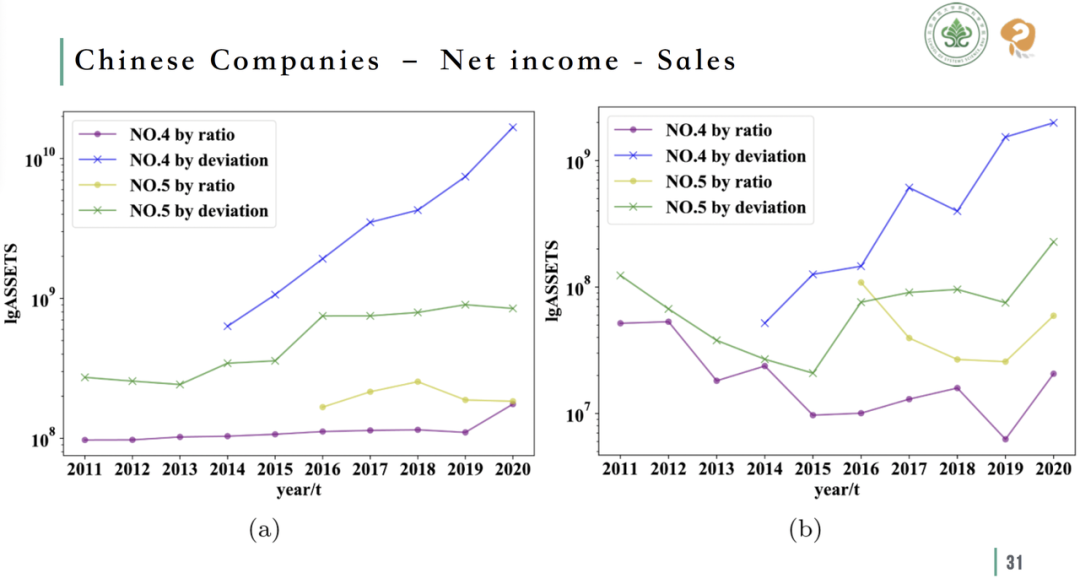

两种指标所选第四、第五公司的未来发展对比

对这两个序列中的第四、第五名企业进行后续跟踪，结果显示，离差指标筛选出的公司未来保持了更好的增长势头。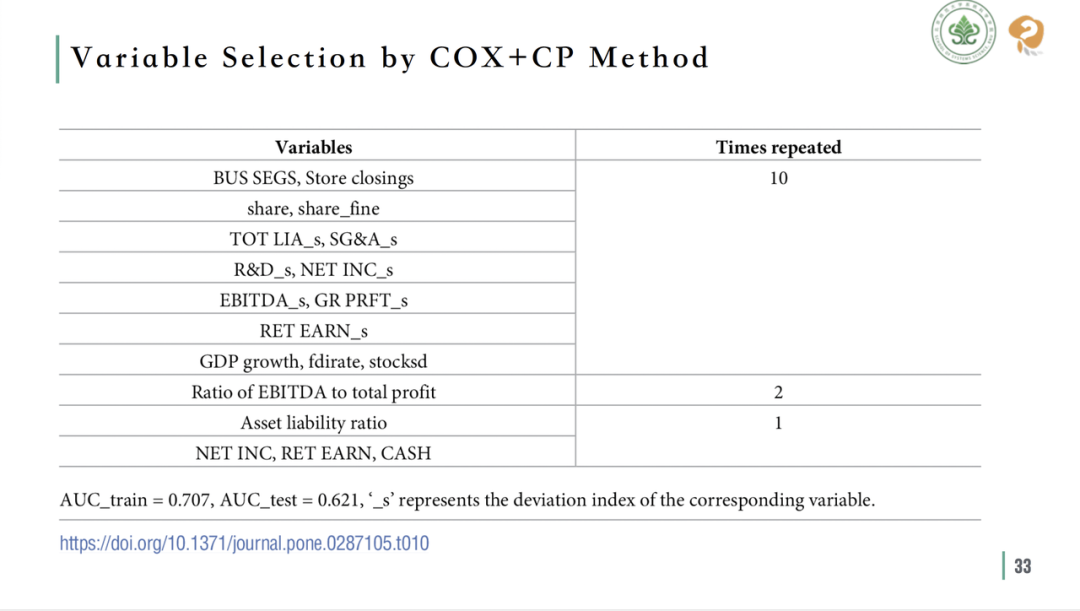

离差指标在大样本中的用例

在更广泛的样本中，该研究通过比较比例指标和离差指标在预测企业破产任务中的效用，进一步验证了离差指标的有效性。在运用COX+CP机器学习 (machine learning) 算法对上百个潜在变量进行分析后，发现大多数对企业破产预测最有帮助的指标几乎都是离差指标。这些结果进一步证明了，在复杂的企业环境中，离差指标提供了一种更为准确和全面的企业评估方法。

3. 公司的生长

3.1 Gibrat 假说：企业生长是一个随机过程

Gibrat假说 (Gibrat’s hypothesis)，由经济学家Robert Gibrat于1931年提出，主张企业的生长是一个完全随机的过程。根据这个假说，企业每年的生长率可以被视为一个均值为零的随机数，这意味着企业生长的快慢不受其初始规模的影响，而是由各种随机因素决定。然而，围绕Gibrat假说的学术讨论十分繁复且混乱。研究文献中，有数百篇论文从不同角度探讨了这一假说的适用性。这些研究涉及到的情况极其复杂，包括不同行业、市场和时间段，使得关于Gibrat假说成立与否的学界观点出现了诸多分歧，该假说的适用性成疑。为了更直观地理解Gibrat假说，张老师团队和合作者模拟了5条曲线来展示Gibrat假说的企业生长过程。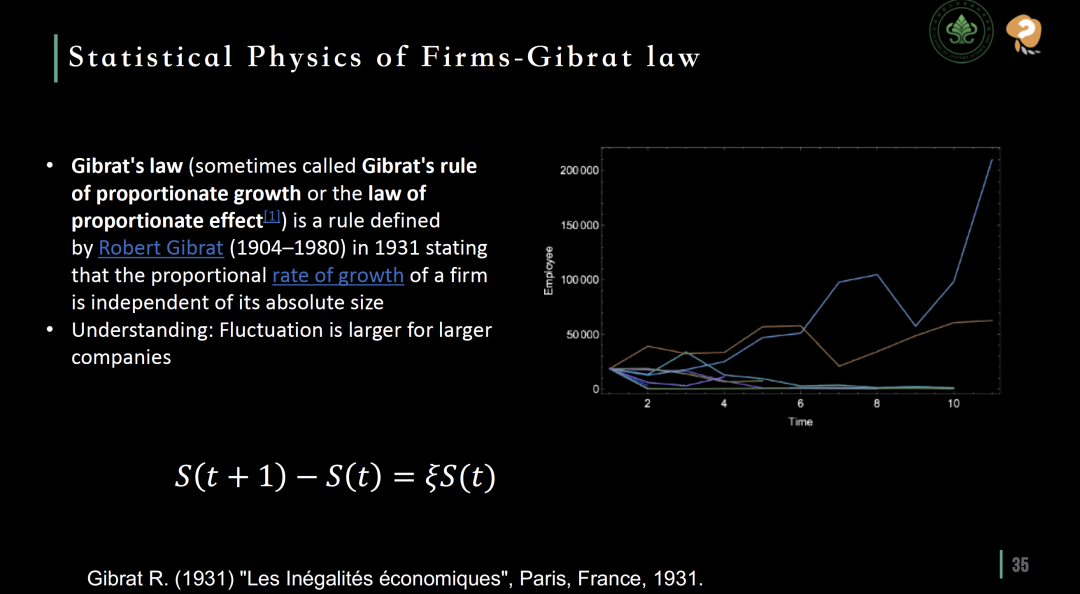

这些曲线在直观上似乎更加符合真实的市场情况。原因在于，企业的规模对于年生长率中的随机性产生了一种放大效应，即使增长率本身是随机的，较大的企业由于其规模庞大，即使细微的生长率变化也可能导致绝对数值上巨大的增长或缩减。因此，这些曲线揭示了企业规模如何影响其生长轨迹的重要性。

3.2 Stanley 的推广：企业的统计物理学

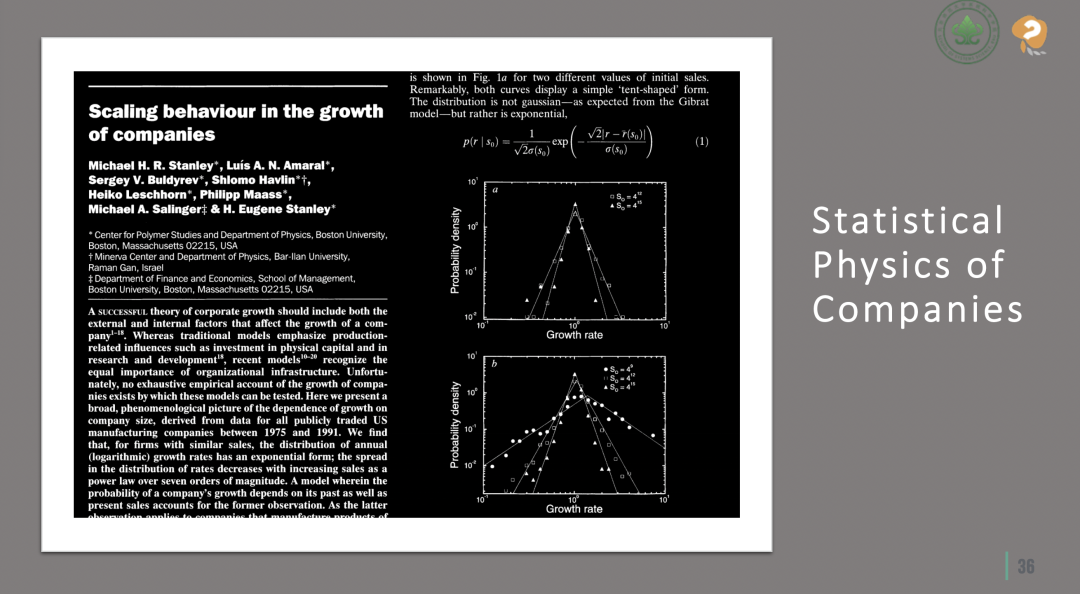
Stanley, M., Amaral, L., Buldyrev, S. et al. Scaling behaviour in the growth of companies. Nature 379, 804–806 (1996). https://doi.org/10.1038/379804a0
物理学家Stanley在深入研究Gibrat假说的基础上，提出了一个新的见解。他指出，虽然企业生长的过程被假设为一个随机的过程，但这个“随机数”本身实际上遵循着一定的规律，尤其是在其方差上体现得非常明显。Stanley认为，企业的规模越大，其生长率的方差——即生长的波动性——就会相对减小。这个观点可以通过一个形象的比喻来理解：如果将企业比作一艘船，那么规模较大的企业就好比一艘大船。正如在海上航行时，大船比小船更能抵御风浪，保持稳定，大型企业也往往能更有效地抵抗市场波动和外部冲击。这种现象的背后原因是多方面的，例如，大企业通常拥有更多的资源和更广泛的市场分布以分散风险。

3.3 从规模法则得到生长方程 (Growth Equation)

尽管Gibrat假说及Stanley的后续研究为理解企业生长提供了重要视角，但它们都未研究过企业生长率随机数均值，其是否遵循某种规律的问题。针对这一空白，张老师课题组和合作者进行了创新性的研究，遵从第一性原理 (First Principle)，从企业的财务平衡出发对企业生长进行分析。
这项研究中摒弃了传统社会学和组织学中以人员数量作为企业规模的衡量标准的习惯，而是选择以企业的总资产作为衡量规模的主要指标。在这个新的框架下，通过对收入、负债和融资 (financing) 三个方面的分析，探究了总资产变化的模式。其中，收入和负债的规模法则已经得到过详细分析，而对于融资，鉴于其在企业资产结构中占比相对较小，可以在初步分析中忽略其影响。这样的方法使得研究避免了引入过多的人为假设，从而更加贴近企业实际运营的真实情况，并发掘企业生长的规模法则当中存在的指数项，恰好对应着债务的超线性规模法则。

企业生长曲线的普遍形式

基于这些研究成果，张老师团队和合作者们进一步推导出了企业的生长方程。这一方程的左边表示企业规模的变化率，而右边则描述了这一变化率与总资产之间的函数关系。通过对方程的近似求解，他们发现企业生长呈现出一种幂律模式，其幂次大约在5～6之间。这一发现揭示了企业的总资产生长可能并非直观想象的指数生长，而是幂律生长。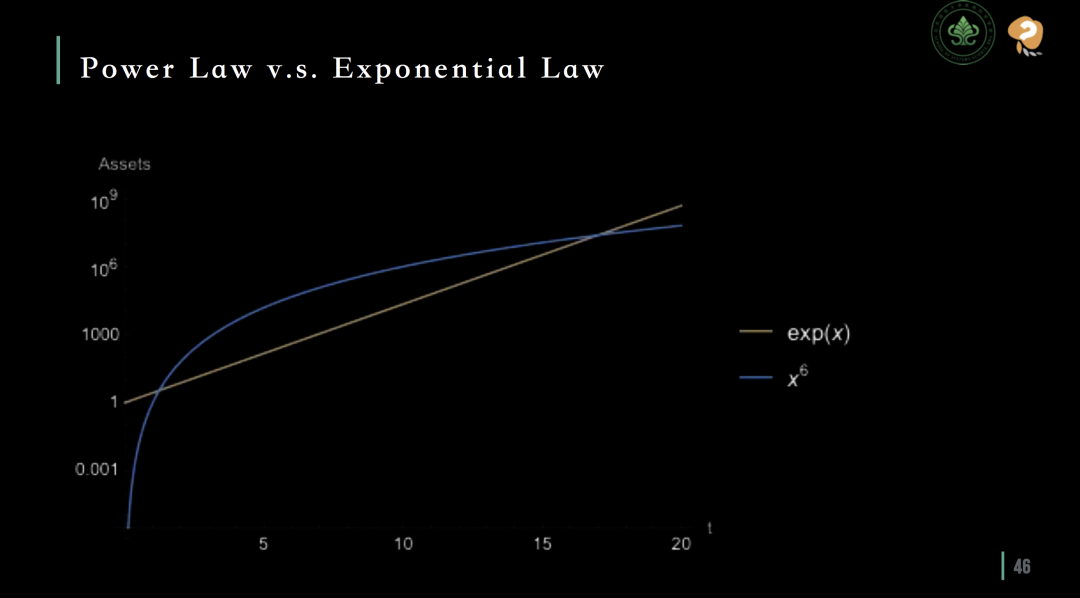

幂律生长 (蓝)与指数生长 (黄)

这两种生长模式之间的区别非常显著。具体来说，幂律生长意味着随着企业规模的增大，其资产生长速度会逐渐放缓。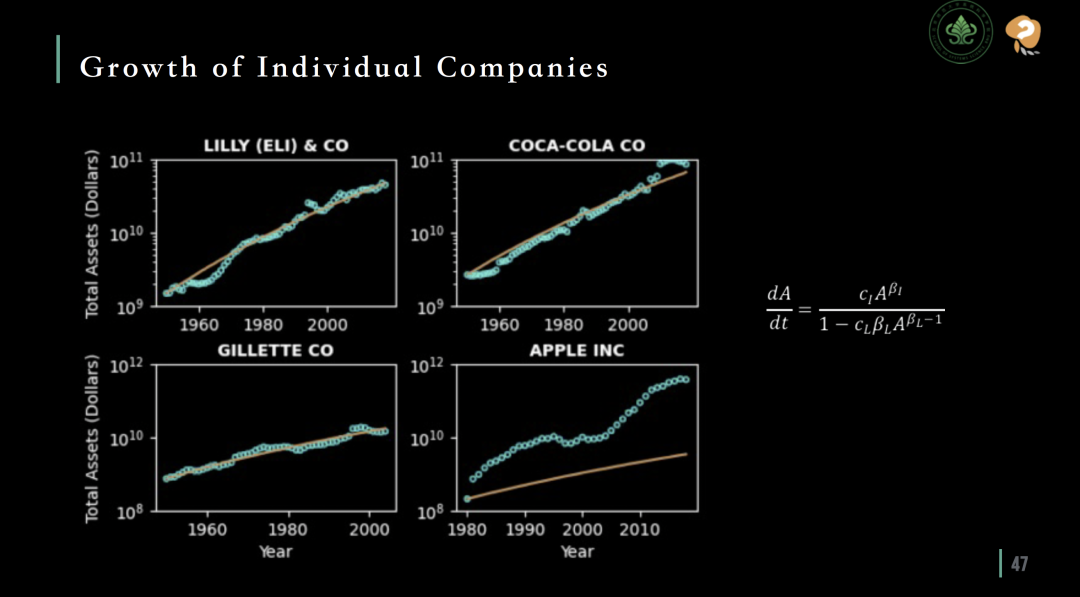

单个公司的生长规律预测吻合情况 (美国企业)

研究还利用超过三万个美国企业的数据进行了验证。结果发现，对于大多数传统公司而言，这一企业生长方程能够较为准确地预测其规模生长。然而，对于苹果公司等高科技企业，其生长速度却显著高于公式预测的水平，这些公司的数据在图表上表现为严重的上偏。除此之外也存在一些下偏的企业，而那些企业通常较为不知名，因此并没有绘制在图中。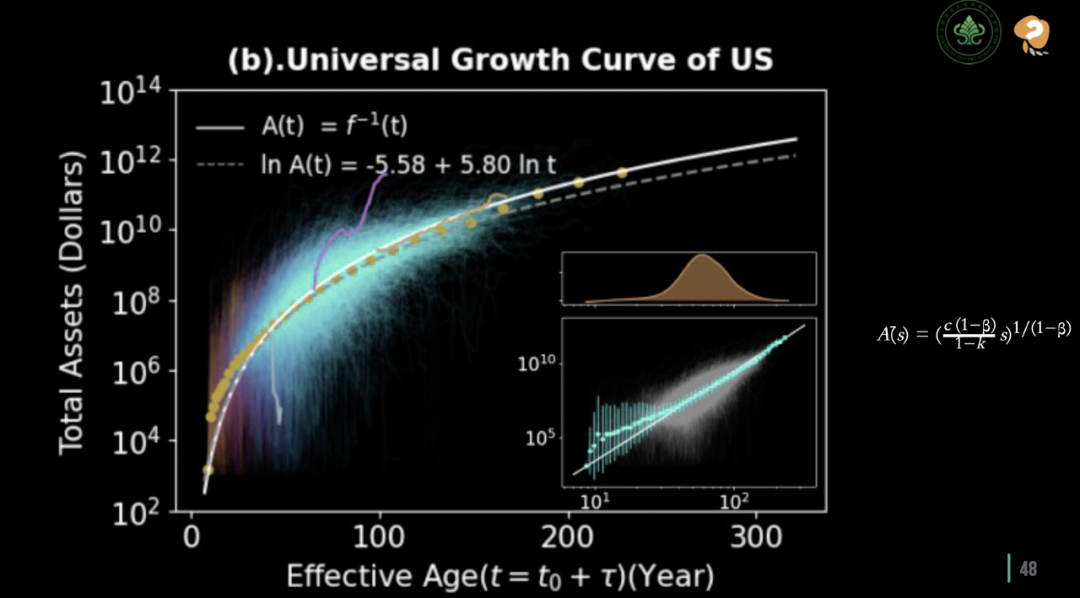

美国企业的Universal生长曲线

在对美国企业的规模变化规律进行深入研究时，将所有企业的数据汇集到一张图上。在这张图中，用一条白色曲线表示的是通过求解生长方程得到的 Universal 生长曲线。通过观察这张图，可以看到许多黄色的圆点恰好落在了白线周围，它们与白线吻合，说明即使在数据解耦的情况下，生长方程仍然能够对大部分企业的规模生长趋势进行较为准确的预测。接着研究团队将同样的分析方法应用于中国市场，对过去30年间的3000多家企业进行了研究。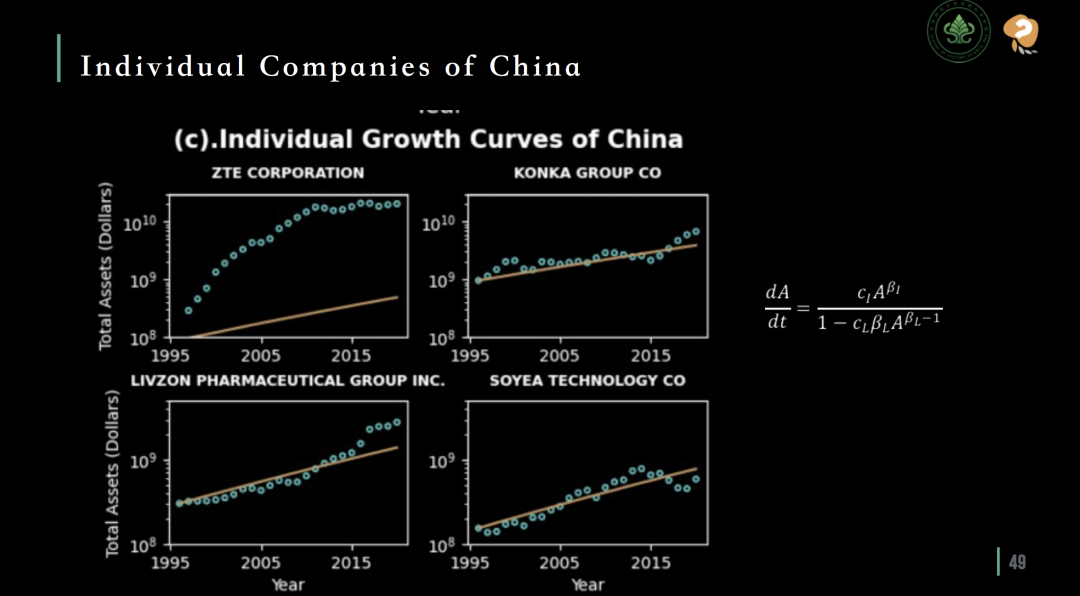

单个公司的生长规律预测吻合情况 (中国企业)

结果发现，与美国市场类似，大多数中国企业的生长数据也符合所绘制的生长曲线。然而，就像在美国市场的情况一样，一些高科技企业的生长数据在曲线上呈现出显著的上偏，即它们的生长速度超过了预测值。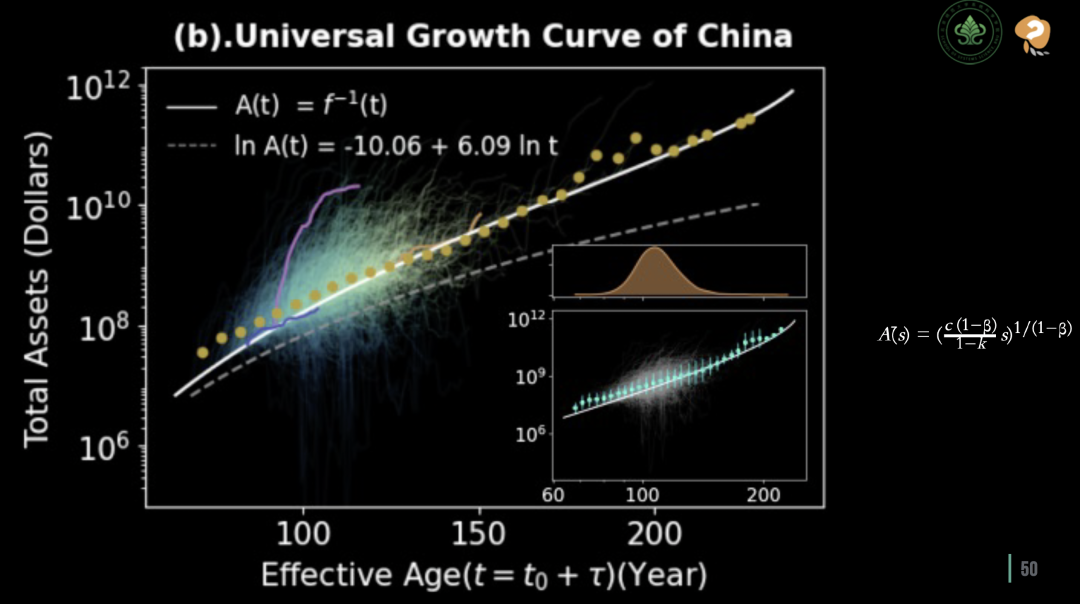

中国企业的Universal生长曲线

进一步对中国企业的 Universal 生长曲线进行分析时，同样可以观察到有许多黄色圆点紧贴着白线，这进一步印证了 Universal 生长曲线的适用性。同时在图中可以留意到，无论是美国还是中国市场，都存在一些离群的企业生长曲线。为了对这些偏离情况进行更精确的分析，研究团队统计了这些偏离的Laplacian分布情况。图表中的横轴表示企业生长数据与全局生长曲线之间的偏差值，而纵轴显示了这种偏离发生的概率。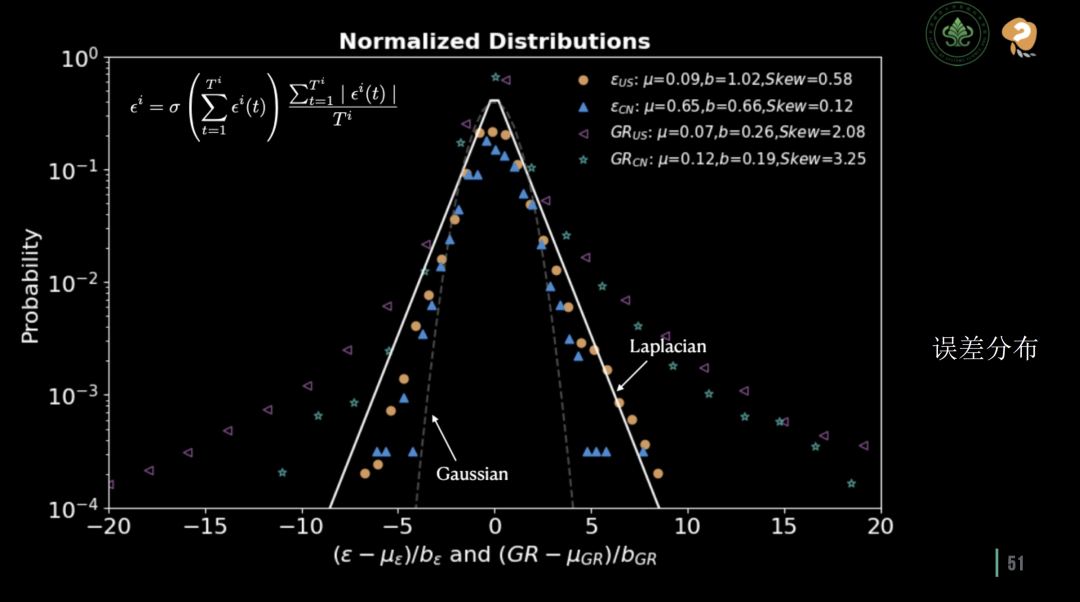

偏离的Laplacian分布

这项研究中，首先将高科技公司这一特殊群体放在一旁，以便更清晰地分析一般企业的生长模式。通过观察所得的Laplacian分布图，可以发现在均值为0处分布呈现出一个显著的高峰。这一发现表明，绝大多数企业的生长实际上都紧密吻合着全局生长曲线。此外，分布形成一个向两侧展开的三角形，这意味着偏离均值越大的情况发生的概率越小，也暗示规模较小的企业更可能出现较大的偏离。
这一研究结果在某种程度上与物理学家Stanley的工作相呼应。Stanley所展示的是类似拉普拉斯“帐篷”形状的分布，但其分布是基于企业生长率的数据，而这些数据实际上表现为右偏。这种偏差的产生，是因为企业生长率的数据中忽略了企业的平均生长率。而在这项研究中，综合考虑了企业的平均生长率，从而更准确地预测了市场的整体生长趋势。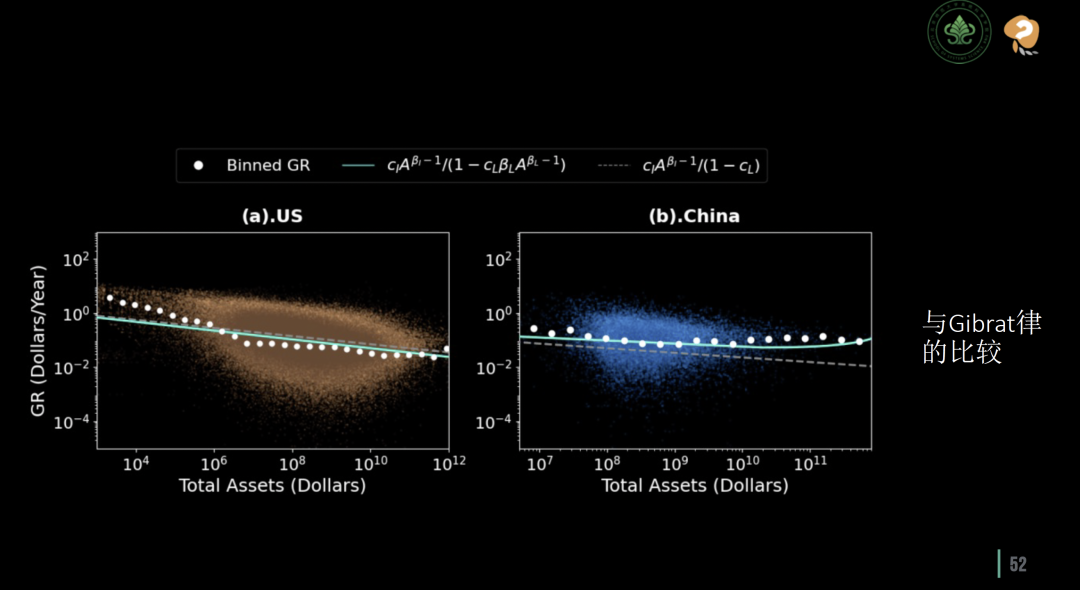

生长曲线对比Gibrat假说

在分析的曲线中可以观察到一些引人入胜的现象：针对美国企业，不难发现当企业规模较小时 (即在图表的左侧)，它们的生长率接近1。这一点揭示了一个重要的事实：小型企业的生长并非完全随机，而是存在一定的规律性。然而，随着企业规模的增大，曲线逐渐变得平缓，生长率逐步降低，接近0。这表明相对于小企业，大型企业的生长趋于随机性。
在对中国企业的分析中可以发现一个不同的趋势，当企业规模生长到一定程度时 (即在图表的右侧)，生长率出现上升。这意味着与美国的企业不同，中国的大型企业在达到一定规模后，其生长率反而呈现上升趋势。这一发现也可以通过之前提到的生长方程进行预测，展示了不同市场环境下企业生长规律的差异性。
从中可以看到，这项研究涵盖了围绕Gibrat假说的几乎所有可能情况，从一定程度上消除了这一领域的争议。

4. 奇点

奇点的诞生

在分析企业的生长方程时，涌现了一个神奇的概念——“奇点” (Singularity)。深入探究企业生长方程时会发现，其在某些条件下将导致分母为零，而这种情况发生时，就意味着理论上此时企业的规模生长率会达到无穷大，这个让企业生长方程分母为零的点便是奇点。这个概念听起来似乎已经脱离了实际，但围绕奇点展开的分析却将揭示关于企业生长的真实洞见。
具体来说，对于那些规模数值逼近奇点的企业而言，它们的生长率会急剧上升。这意味着，这些企业的规模将迅速扩大，快速越过奇点，而不会在奇点处停留。在实际的市场表现上，这可能意味着企业的总资产在某一年突然大幅生长。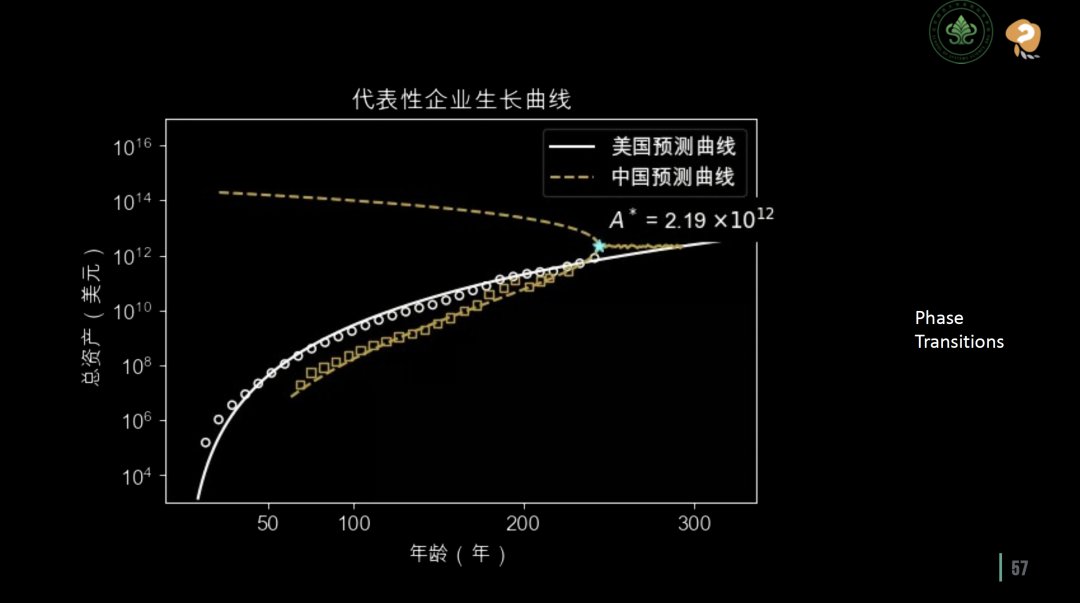

中国企业的临界规模

对中国市场的分析显示，企业的总资产规模在接近奇点时会经历反复的波动。这个现象的出现，取决于企业的资产负债率随着规模生长的变化情况，只有当该国的债务规模法则幂指数大于1时，奇点才会出现在该国的市场。根据之前提到的幂次为1.09的中国企业资产负债幂律曲线，从中可以推断中国企业群体中存在奇点。通过分析直至2020年的数据，计算得到这个奇点的理论值为10的12次方，这可以被视为中国企业生长的理论上限，也就是所谓的 “临界规模” (Critical Scale)。
然而，需要注意的是，临界规模并非一个固定不变的值。债务规模法则的幂指数βL——这一本质上是动态变化的指数——在之前的预测分析中被假设为了一个常数，而实际上已经有不少中国企业突破了这一理论天花板，这表明这种常数假设可能将不再适用。因为中国政府近年来对中小企业的扶持政策，例如发放债券等，可能会使得债务幂指数βL逐渐降低，从而使得所谓的天花板变得更为模糊直至消失。
在美国市场的情况也证明了临界规模的动态属性。在70、80年代，美国市场的幂指数通常大于1，但随着布雷顿森林体系的崩溃和美元与黄金脱钩等一系列金融事件，美国市场的幂指数逐渐下降至接近于1，从而逐步消除了奇点的存在。这清楚地表明，宏观经济政策和市场环境的变化对于这个幂指数有着深远的影响，继而决定着奇点的存在与否。

5. 结语

本次读书会通过规模法则分析了企业生长的普遍规律，为企业的可持续发展提供了新的视角和策略。
首先，本次分享介绍了规模法则，它揭示了复杂系统中变量随系统规模扩大而变化的规律，其表现形式为幂律生长，之后便通过介绍规模法则在生物学、城市规划等领域的应用，展示了规模法则强大的普适性。
接下来，用规模法则分析了企业的规模生长过程，揭示了其中的确定性规律，从多维度展开讨论了企业这一复杂系统的性质。随后，通过研究企业的规模与其营业额、成本等指标之间的关系，我们可以发现企业生长的普遍规律。紧接着，介绍了从企业生长第一性原理出发的生长方程，这些理论为理解企业生长提供了重要视角。通过分析美国和中国市场的企业数据，发现大多数企业的生长数据符合生长方程所对应的生长曲线，不过高科技企业的生长速度往往高于预测值。
此外，读书会还探讨了企业生长过程中存在的“奇点”，这揭示了在特定市场环境下，企业的生长存在理论上限，即临界规模。然而，临界规模并非固定不变，受宏观经济政策和市场环境的影响。

扫描下方二维码，观看读书会回放视频https://pattern.swarma.org/study_group_issue/543

学者简介

张江：北京师范大学系统科学学院教授，集智俱乐部、集智学园、集智科学研究中心创始人，曾任腾讯研究院、华为战略研究院等特聘顾问。主要研究领域包括复杂系统分析与建模、规模理论、机器学习等。

相关阅读：

• 张江新书发布！《规模法则——探索从细胞到城市的普适规律》
• 复杂物理学是可能的吗？｜《规模法则》新书试读
• 万物的规模——《规模法则》的探索之旅
  

复杂系统管理学读书会第二季

21世纪人类已经进入了全球化时代，事物彼此之间的依赖程度愈来愈深，传统的分割式思维模式已经无法深入分析与解决现有问题。在此时代背景下，一种主张以系统思维模式为核心的科学管理理论顺势而起。

兴起于20世纪80年代的复杂性科学，是系统科学发展的新阶段，也是当代科学发展的前沿领域之一。复杂性科学的发展，不仅引发了自然科学界的变革，而且也日益渗透到哲学、人文社会科学领域。英国著名物理学家霍金称“21世纪将是复杂性的世纪”。

企业、组织都是典型的复杂系统，也是复杂科学可以落地的方向。复杂系统管理学，是建构在复杂系统基础上发展的管理学新视角。复杂系统视角不仅可以形成一个认识问题的体系，也可以孕育解决问题的思维方式和方法。它不只是一堆解释性的概念，也可以通过与社会科学和大数据相结合，发展算法、构建模型，完成理论验证，发展出可预测未来的动态演化模型。

集智俱乐部邀请了清华大学社科学院社会科学院与公共管理学院合聘教授罗家德，清华大学经济管理学院副教授张勉，SIMOE 和奇弦智能创始人、同济大学组织仿真中心主任陆云波，以及东南大学经济管理学院教授吕鸿江共同发起了复杂管理学读书季第二季。聚焦在自组织、DAO、创新型管理、网络等方向，分享复杂系统管理领域的前沿理论、经典科普图书，旨在促进学术交流、知识分享以及跨领域合作。共同探讨复杂科学理论在复杂系统管理场景的应用、实践与展望，一起应对复杂多变的人类发展未来。

本系列读书会采用线上和线下相结合的方式，2023年9月23日开始，每周六下午 14:00-17:00，持续时间预计8-10周。读书会详情及参与方式见后文。

详情请见：

生态型组织进化：混沌边缘的涌现｜复杂系统管理学读书会第二季启动

推荐阅读

1. 张江新书发布！《规模法则——探索从细胞到城市的普适规律》2. 复杂物理学是可能的吗？｜《规模法则》新书试读3. 公司规模及其偏离：企业评估和破产预测的新指标4. 张江：第三代人工智能技术基础——从可微分编程到因果推理 | 集智学园全新课程5. 成为集智VIP，解锁全站课程／读书会6. 加入集智，一起复杂！

点击“阅读原文”，报名读书会