
导语
从原子到生命到浩瀚宇宙,物理系统中的许多现象涉及到广阔的尺度。重整化群(renormalization group)是在不同尺度下考察物理系统变化的数学工具,帮助我们理解系统在不同尺度下的行为。为了纪念物理学家 Kenneth Wilson 提出重整化群理论大约50年,近期 Nature Physics 推出评论文章合集,在其中一篇文章中,美国 IBM T. J. Watson 研究中心研究员涂豫海介绍了利用重整化方法研究非平衡集群(flocking)的研究,并认为将粗粒化和重整化群的基本思想引入活性系统和生命系统的研究中,是物理学和生物学中最有前景的方向之一。
研究领域:统计物理,非平衡系统,重整化群,集群行为,随机动力学 涂豫海 | 作者黄泽豪 | 译者梁金 | 审校
涂豫海 | 作者黄泽豪 | 译者梁金 | 审校

论文题目:The renormalization group for non-equilibrium systems论文地址:https://www.nature.com/articles/s41567-023-02196-z
Ken Wilson 在重整化群理论方面的工作源于对平衡系统中临界现象的研究(有关Wilson对该主题的评论,请参见参考文献[1])。重整化群方法产生了即刻和持久的影响。然而,在1982年底诺贝尔奖颁奖典礼的演讲中,Ken Wilson 指出:“在我看来,使用重整化群和展开完成的大量研究只是一个开始,未来二十年(或者可能需要下一个世纪)人们将发现更大范围的应用研究的。”在这篇评论中,我将描述我自己在发展一种这样的应用方面的实践:非平衡随机动力系统(non-equilibrium stochastic dynamical systems)的研究。
1. 重整化群用于研究集群现象
Leo Kadanoff 和 Ken Wilson 对重整化群理论的最初发展是基于平衡系统的。在这些情况下可以写出控制系统统计特性的哈密顿量。
基本思想是在粗粒化水平上考虑多体系统,即在一个更大的长度尺度上对微观自由度做平均。Kadanoff提出 [2],经过适当的缩放后,粗粒化系统可以用与初始模型相同形式的哈密顿量和一组重整化参数描述。参数从更精细的尺度到更粗糙的尺度的变换构成重整化群(renormalization group)。
反复应用这种粗粒化过程会产生所谓的参数流。这个流具有不动点(fixed point)——在重整化下保持不变的特殊值。这些参数对应于该系统遵循的普适标度律的临界点。具有相同标度律的系统被认为属于同一个普适类(universality class)。 图1. 重整化群方法示意图
图1. 重整化群方法示意图
重整化群理论中的另一个关键思想是上临界维数的存在。超过这个维度,与平均场理论相对应的不动点是稳定的,这意味着它正确地捕捉到了临界行为。对于较低的维度,可以通过微扰求解阶的重整化群方程来得到阶的标度指数,从而找到临界行为的近似值 [3]。
随后的研究很快将重整化群的应用扩展到了临界现象的动力学研究中[4,5](相关研究的全面综述,请参见参考文献[6])。虽然重整化群最初是在平衡系统中发展起来的,但很明显,动态重整化群可被用于研究没有哈密顿量或其他能量泛函的非平衡系统的随机动力学。这是重整化群的一个非常令人兴奋的特点,因为自然界中的大多数系统都受外力驱动而远离平衡态,但它们表现出与在平衡临界现象中观察到的类似的鲁棒的标度行为。
一个这样的例子是用于描述界面生长的 Kardar-Parisi-Zhang (KPZ) 方程 [7]。在KPZ方程的情况下,重整化群已被成功地用于理解其标度行为 [7-9]。从个人角度来说,研究KPZ方程及其变化使我有机会学习和欣赏重整化背后美妙的直觉和强大的技术[10,11]。后来,我与John Toner合作,发展了一个关于集群的流体动力学理论,其中重整化群方法发挥了关键作用。
2. 重整化群用于研究集群现象
最容易辨别的集群现象出现在鸟群和鱼群中(图2a,b)。但是,这种集体运动也可以在较小的长度尺度上出现,例如在菌群(图2c)或马达蛋白和微管的混合物中。
图2. 大自然中的集群现象。集群行为跨越巨大的长度范围,从(a)鱼群和(b)鸟群中的数十米到数百米,再到(c)菌群中的微米级别。
尽管集群出现在许多日常情境中,但直到过去29年,它的许多普遍特征才被发现和理解。这种理解在很大程度上来自统计物理的思想,这些思想被应用在由 Tamas Vicsek 及其合作者,John Toner和我,进行的一系列研究中。
John 和我在1994年末开始了集群理论的研究,那是 Tamas Vicsek 访问位于纽约约克镇高地的 IBM Watson 实验室期间。Vicsek 举办了一个关于活性自驱动智能体(active self-driven agents)集群模型(称作 boid [12])的研讨会。每一个 boid 以恒定速度移动,其移动方向由其邻居运动方向的平均值加上一些噪声决定。在他们对模型的二维模拟中,Vicsek 及其合作者研究了当降低噪声水平或增加物体密度时会发生什么。他们观察到了从无序相到有序相的相变,在无序相中,智能体在没有长程序的情况下沿随机方向移动,在有序相中,它们一致地聚集成一个集群。
在报告的最后,Vicsek 抱怨说,他无法发表他的研究成果,因为审稿人坚持认为具有长程序的集群状态在二维情况下是不可能的,因为它违背了Mermin-Wagner定理[13]。该定理指出,在二维或更低维度的模型中,具有短程相互作用的有限温度系统的连续对称性无法被破坏。
这个结果似乎意味着任何有限的噪音都会产生涨落,破坏具有连续对称性和短程相互作用的系统的长程序。Vicsek 模型就属于这一类,有序态的单个集群方向破坏了模型的旋转对称性。以此看来,至少在两维,自发形成的集群注定会消失。
在Vicsek的研讨会上,作为听众的John和我都提出了很多问题。Vicsek的模拟结果令我们感到困惑,我们决定立即共同解决这个问题——也许紧迫性来自于希望将 boid 集群从在二维空间中看似不可避免地分开的命运中拯救出来。当John和我在第二天重聚时,我们已经掌握了粗粒化流体动力学理论的基本要素。在接下来的几个月里,我们与Vicsek保持着联系,在集群理论上取得更多进展,Vicsek的论文最终在1995年发表[14]。大家不禁猜测,我们的工作可能对此有一定帮助。
John和我发展的集群流体动力学理论基于 boid 的速度场(v)的双重作用。首先,模型的相互作用试图让 boid 的速度与其邻居的速度保持一致,这可以用描述磁性材料的一个被称为矢量 ϕ4 理论的模型来描述。其次,速度矢量还表征了 boid 的物理运动,它既输运 boid 的主体又输运 boid 的速度。这种输运和流动可以通过Navier-Stokes方程来描述。
结合这两个要素,我们写下了一个动力学场方程,其中既有输运的对流项 ((v·∇)v) ,也有海森堡自旋的标准 ϕ4 类型项。后来,我们扩展了该方程,使其包含所有可能的相关项,这些项保持了速度和空间的旋转对称性,而不施加伽利略不变性。伽利略不变性因为 boid 群移动的介质(空气或水)是唯一的参考系而被破坏。这个描述集群流体动力学特性的方程现在被称为Toner-Tu方程。值得强调的是,由于速度场的双重作用,集群系统本质上是远离平衡态的,因为没有能量泛函可以既描述 boid 动力学的方向一致性又描述其物理运动。
我们用重整化群技术对流体动力学理论的分析在Vicsek的论文[14]发表的几个月后发表[15]。在所有 boid 都朝着同一个方向移动的有序相中,可以通过计算有序态周围的涨落幅度来评估系统的稳定性。对称性的破缺意味着存在被称为Goldstone模(Goldstone mode)的长波长、低能量的自由度,这些自由度可以被噪声源激发。
由于Goldstone模的存在,有序态周围的速度涨落的方差包含一个标度为 L2χ 的项,其中L是系统的长度尺度。我们发现,在非线性对流项不存在的情况下,χ=1-d/2,其中d是系统的维数。在三维以下,涨落随着系统尺寸的增加而增长,有序态不稳定,符合 Mermin-Wagner 定理的预测。
然而,集群系统中 boid 群的运动使问题与受 Mermin-Wagner 定理约束的平衡模型完全不同。特别地,我们发现对流项影响了模型的重整化群流,并且指数χ偏离了其在线性理论中的值。事实上,通过使用模型的某些应该适用于d = 2 的不变性质,我们能够得到一个精确的表达式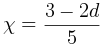 。
。
我们的结果表明,当 d = 2 时,χ = −1/5 < 0,长程有序态周围的涨落在热力学极限下仍然是有限的,集体集群行为在二维中是稳定的。随后,我们应用集群的流体动力学理论研究了其他重要的涌现现象,例如声波[16]和集群的巨大数量涨落[17]。最近,动力学重整化群方法已被用于研究在淬火无序(quenched disorder)[18]和自然集群(natural swarms)中的集群行为[19]。集群模型在物理学以外的领域也产生了影响,从机器人学[20]到交通[21]等。
3. 引入非平衡生物系统
除集群外,基于重整化群的方法的多功能性和强大性已在诸如活性物质和生命系统在内的不同非平衡系统中得到了证明。例如,它已经被用于开发[22]一种粗粒化方法,来研究大型神经元网络中的神经活动,该方法揭示了大脑不同部位神经元放电模式的准普适标度行为[23]。我们最近的工作中构建了一种态空间方法,来理解非平衡反应网络中不同尺度上的能量耗散率的逆幂律标度[24,25]。 图3. 重整化群方法用于神经科学研究。|来源:Tiberi et al.
图3. 重整化群方法用于神经科学研究。|来源:Tiberi et al.
非平衡生物系统经常表现出与平衡态生物系统截然不同的意想不到的行为。然而,与平衡态统计物理模型一样,它们在不同尺度上表现出集体行为。我相信将粗粒化和重整化群的基本思想引入活性系统和生命系统的研究中,是物理学和生物学中最有前景的研究方向之一。
核心概念
重整化群
在理论物理中,重整化群(renormalization group,简称RG)是一个在不同尺度下考察物理系统变化的数学工具。标度上的变化称为“标度变换”。重整化群与“标度不变性”和“共形不变性”关系紧密,都与自相似有关。在重整化理论中,系统在某一个标度上自相似于一个更小的标度,但描述它们组成的参量值不相同。系统的组成可以是原子,基本粒子,自旋等。系统的变量是以系统组成之间的相互作用来描述。
热力学平衡态
热力学平衡态指一个热力学系统在没有外界影响的条件下,系统各部分的宏观属性(如物质的量、能量、体积等)在长时间内不发生任何变化的状态。
临界维数
在物理学中相变的重整化群分析中,临界维数是相变特征发生变化的空间维度。在临界维数以下没有相变。在临界维数以上,该理论的临界指数与平均场论中的临界指数相同。V.Ginzburg提出了一个在平均场论中获得临界维数的优美准则。
Kardar-Parisi-Zhang方程
在数学中,Kardar–Parisi–Zhang(KPZ)方程是一个非线性随机偏微分方程,由Mehran Kardar、Giorgio Parisi和Yi-Cheng Zhang于1986年提出。它描述了作为空间和时间坐标的函数的高度场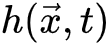 随时间的变化。
随时间的变化。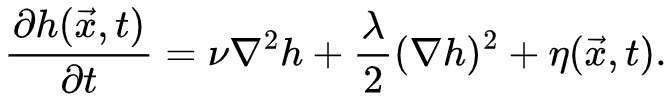
其中,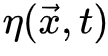 是白高斯噪声。
是白高斯噪声。
通过重整化群,KPZ方程被推测为许多表面生长模型的场论,如Eden模型、弹道沉积(ballistic deposition)和弱不对称单步固体对固体过程(SOS)模型(weakly asymmetric single step solid on solid process model)。Bertini和Giacomin在SOS模型的情况下给出了这一推测的一个严格证明。
Mermin-Wagner定理
在量子场论和统计力学中,Mermin–Wagner定理(也称为Mermin–Wagner–Hohenberg定理、Mermin–Wagner–Berezinskii定理或Coleman定理)指出,在d≤2维度具有足够短程相互作用的系统中,连续对称性在有限温度下不能自发破缺。直观地说,这意味着可以在几乎没有能量消耗的情况下产生长程涨落,而且由于它们增加了熵,系统倾向于产生。这是因为,如果发生这种自发的对称性破缺,那么相应的无质量Goldstone玻色子将具有红外发散的关联函数。
David Mermin、Herbert Wagner(1966)和Pierre Hohenberg(1967)在统计力学中以及Sidney Coleman(1973)在量子场论中严格证明了d≤2维无限系统中不存在自发对称性破缺。该定理不适用于离散对称性,这可以在二维伊辛模型中看出。
Vicsek模型
Vicsek模型是一种用于描述活性物质的数学模型。物理学家研究活性物质的一个动机是与该领域相关的丰富现象学。集体运动和集群是研究最多的现象之一。在为从微观描述中捕捉这种行为而开发的大量模型中,最著名的是Tamás-Vicsek等人1995年引入的模型。
物理学家对这个模型非常感兴趣,因为它是最小的并且描述了一种普适性。它由点状自推进粒子组成,这些粒子以恒定的速度演化,并在存在噪音的情况下使其速度与邻居的速度一致。这样的模型显示了对齐后的高密度粒子或低噪声下的集体运动。
学者简介
 涂豫海,1987年毕业于中国科学技术大学,1991年在加州大学圣地亚哥分校获得物理学博士学位。1991年至1994年,他是加州理工学院的 Division Prize Fellow,1994年加入IBM沃森研究中心担任研究员,并于2003-2015年担任理论组组长。他自2004年起担任美国物理学会(APS)会士,并于2017年担任美国物理学会生物物理部主席。他也是美国科学促进会(AAAS)会士。
涂豫海,1987年毕业于中国科学技术大学,1991年在加州大学圣地亚哥分校获得物理学博士学位。1991年至1994年,他是加州理工学院的 Division Prize Fellow,1994年加入IBM沃森研究中心担任研究员,并于2003-2015年担任理论组组长。他自2004年起担任美国物理学会(APS)会士,并于2017年担任美国物理学会生物物理部主席。他也是美国科学促进会(AAAS)会士。
他的研究兴趣包括非平衡统计物理、生物物理、理论神经科学以及近期的深度学习理论基础。其中对生物物理学的研究兴趣有两个方面:通过使用物理学的工具(计算建模、统计物理、动力系统分析)来理解重要的生物现象(如信号转导);从对生物系统的研究中揭示一般的设计原理和新的物理学(如非平衡热力学、随机动力学)。当前的研究兴趣之一是理解生命系统中信息处理的动力学。
他在多个领域做出了开创性贡献,包括集群理论、细菌趋药性(bacterial chemotaxis)的定量模型、昼夜节律时钟(circadium clock)以及生物系统中的能量-速度-精度关系。由于在理论统计物理方面的工作,他与John Toner和Tamas Vicsek一起被美国物理学会授予2020年Lars Onsager奖:“因为他在集群理论方面的开创性工作,这标志着活性物质领域的诞生,并对其发展做出了巨大贡献。”
学者主页:
https://researcher.draco.res.ibm.com/researcher/view.php?person=us-yuhai
参考文献
1. Wilson, K. G. Rev. Mod. Phys. 47, 773–840 (1975).2. Kadanoff, L. P. Phys. Phys. Fiz. 2, 263–272 (1966).3. Wilson, K. G. & Fisher, M. E. Phys. Rev. Lett. 28, 240–243 (1972).4. Halperin, B. I., Hohenberg, P. C. & Ma, S.-k Phys. Rev. Lett. 29, 1548–1551 (1972).5. Bausch, R., Janssen, H. K. & Wagner, H. Z. Phys. B Condens. Matter 24, 113–127 (1976).6. Hohenberg, P. C. & Halperin, B. I. Rev. Mod. Phys. 49, 435–479 (1977).7. Kardar, M., Parisi, G. & Zhang, Y.-C. Phys. Rev. Lett. 56, 889–892 (1986).8. Medina, E., Hwa, T., Kardar, M. & Zhang, Y.-C. Phys. Rev. A 39, 3053–3075 (1989).9. Canet, L., Chaté, H., Delamotte, B. & Wschebor, N. Phys. Rev. Lett. 104, 150601 (2010).10. Kessler, D. A., Levine, H. & Tu, Y. Phys. Rev. A 43, 4551–4554 (1991).11. Tu, Y. Phys. Rev. Lett. 73, 3109–3112 (1994).12. Reynolds, C. W. SIGGRAPH Comput. Graph. 21, 25–34 (1987).13. Mermin, N. D. & Wagner, H. Phys. Rev. Lett. 17, 1133–1136 (1966).14. Vicsek, T., Czirók, A., Ben-Jacob, E., Cohen, I. & Shochet, O. Phys. Rev. Lett. 75, 1226–1229 (1995).15. Toner, J. & Tu, Y. Phys. Rev. Lett. 75, 4326–4329 (1995).16. Tu, Y., Toner, J. & Ulm, M. Phys. Rev. Lett. 80, 4819–4822 (1998).17. Toner, J. & Tu, Y. Phys. Rev. E 58, 4828–4858 (1998).18. Chen, L., Lee, C. F., Maitra, A. & Toner, J. Phys. Rev. Lett. 129, 188004 (2022).19. Cavagna, A. et al. Nat. Phys. 19, 1043–1049 (2023).20. Gazi, V. & Passino, K. IEEE T. Automat. Contr. 48, 692–697 (2003).21. Helbing, D. Rev. Mod. Phys. 73, 1067–1141 (2001).22. Meshulam, L., Gauthier, J. L., Brody, C. D., Tank, D. W. & Bialek, W. Phys. Rev. Lett. 123, 178103 (2019).23. Morales, G. B., di Santo, S. & Muñoz, M. A. Proc. Natl Acad. Sci. USA 120, e2208998120 (2023).24. Yu, Q., Zhang, D. & Tu, Y. Phys. Rev. Lett. 126, 080601 (2021).25. Yu, Q. & Tu, Y. Phys. Rev. E 105, 044140 (2022).
(参考文献可上下滑动查看)
生命复杂性系列读书会
生命是什么?生命怎样起源?生命怎样演化?这些是对生命现象的本质追问,除了传统的生物学研究,如今有大量来自信息、物理、计算机领域的工具方法,正在揭开生命复杂性谜题。基于此,集智俱乐部策划“生命复杂性”系列读书会,自2020年11月5日至今,近百名在从事相关问题研究的老师同学或感兴趣的朋友参与。
了解读书会具体规则、报名读书会请点击下方文章:
因果涌现社区
跨尺度、跨层次的涌现是复杂系统研究的关键问题,生命起源和意识起源这两座仰之弥高的大山是其代表。因果涌现理论、机器学习重整化技术、信息论或信息分解等近年来新兴的理论与工具,有望破解复杂系统的涌现规律。
集智俱乐部因果涌现读书会目前已经进行了三季。第一季读书会系统地梳理了因果涌现的概念,以及它与Sloopy Model、复杂性阈值、自指等概念之间的联系,也探讨了因果涌现理论在复杂网络、机器学习中的应用。参看:因果涌现读书会启动:连接因果、涌现与自指——跨尺度动力学与因果规律的探索。
第二季读书会探讨了涌现、因果科学和机器学习三大主题的融合,包括信息论拓展、因果涌现理论、因果表示学习、多尺度机器学习动力学建模。请参看:因果、涌现与机器学习:因果涌现读书会第二季启动。
第三季读书会进一步围绕因果涌现的核心问题「因果涌现的定义」以及「因果涌现的辨识」进行深入学习和讨论,对 Erik Hoel 提出的 Causal Emergence,Causal Geometry 等因果涌现的核心理论进行探讨和剖析,并详细梳理其中涉及到的方法论,包括从动力学约简、隐空间动力学学习等其他领域中学习和借鉴相关的研究思路,最后探讨因果涌现的应用,包括基于生物网络、脑网络或者涌现探测等问题展开扩展,发掘更多的实际应用场景。请参看:因果涌现读书会第三季启动:深入多尺度复杂系统核心,探索因果涌现理论应用
此次读书会主题是「新信息论:从分解到整合」,是因果涌现系列读书会的第四季,将重点梳理信息分解与整合信息论的相关研究。请参看:新信息论:从分解到整合|因果涌现读书会第四季启动
因果涌现社区聚集了600+成员,积累了大量论文解读资料。欢迎感兴趣的朋友报名,加入因果涌现社区,解锁对应录播权限。
因果涌现读书会回放视频第一季:https://pattern.swarma.org/study_group/7第二季:https://pattern.swarma.org/study_group/16第三季:https://pattern.swarma.org/study_group/28第四季:https://pattern.swarma.org/study_group/35
推荐阅读
1. Nature Physics:重整化群——理解异构网络的显微镜2. 重整化群:从微观到宏观,不同尺度的现象如何联系起来?3. 人脸和宇宙是啥关系?看物理学家怎样用重整化群流模型重新理解视觉4. 张江:第三代人工智能技术基础——从可微分编程到因果推理 | 集智学园全新课程5. 成为集智VIP,解锁全站课程/读书会6. 加入集智,一起复杂!
点击“阅读原文”,报名读书会



 ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง
ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง


