博士论文 | 神经最优传输用于动力学系统：生物医学中的方法与应用 239页

对动力系统的建模是许多科学学科的核心主题，因为它允许我们预测未来的状态，了解复杂的时间交互，并使得决策更加明智。特别是生物系统，它们由动力过程控制，其固有的复杂且不断变化的交互和行为模式。单细胞生物学已经彻底改变了生物医学研究，因为它允许我们在前所未有的规模上监测这些系统。与此同时，它也带给我们巨大的挑战：尽管单细胞高通量方法经常产生数百万的数据点，但它们是破坏性的测验，因此不能对同一个细胞进行两次观察或随时间进行分析。由于该领域许多最为迫切的问题涉及对异质细胞群体对各种刺激（如治疗药物或发展信号）的动态反应进行建模，因此迫切需要提供能够规避该限制并重新对齐这些未配对测量的计算方法。最优传输(OT)已经成为填补这一空白的一个重要机会，因为它允许我们重建分布是如何演化的，只给定不对齐的数据点的不同快照。然而，经典的OT方法不能泛化到未见过的样本。

但当预测即将到来的患者样本的治疗反应或超出测量范围的细胞动态时，这是至关重要的。通过利用OT的理论结构，这篇论文探索和开发了用于阐明生物群体复杂动态的神经静态和动态最优传输方案。它封装了一系列算法框架，对群体动态的理解和预测都有所贡献：首先，我们推导出能够学习未受扰和受扰细胞之间未配对分布之间映射的静态神经最优传输方案。这些模型擅长预测对不同扰动的单细胞反应，如癌症药物筛选，并将治疗结果的推断泛化到未观察到的细胞类型和患者。这对个性化医疗有重要意义，因为它允许在大规模的临床研究中预测新患者的治疗反应。

其次，我们探索了利用OT与部分微分方程和通过Jordan-Kinderlehrer-Otto方案的梯度流，以及通过扩散薛定谔桥的随机微分方程和最优控制的联系的动态神经最优传输公式。这些方法随后作为从边际观察中重建随机和连续时间动态的强大工具，允许我们剖析细粒度和时间分辨的细胞机制。

这篇论文将众多看似无关的概念连接成一个统一的框架，所呈现的方法为细胞动态的建模提供了计算和数学基础。这为了解细胞异质性、可塑性和反应景观提供了新的途径。这种对静态和动态OT的神经参数化允许对样本之外的推断，为发现新的生物学现象、从单细胞患者样本中推断个性化治疗方法和推动再生医学的边界提供了令人兴奋的机会。

论文题目：Neural Optimal Transport for Dynamical Systems: Methods and Applications in Biomedicine

作者：Bunne Charlotte

类型：2023年博士论文

学校：Eidgenössische Technische Hochschule Zürich，ETH Zurich（瑞士苏黎世联邦理工学院）

下载链接：

链接: https://pan.baidu.com/s/1v8LV3gUJE-2I4vKKqkbE8A?pwd=f993

硕博论文汇总：

链接: https://pan.baidu.com/s/1Gv3R58pgUfHPu4PYFhCSJw?pwd=svp5

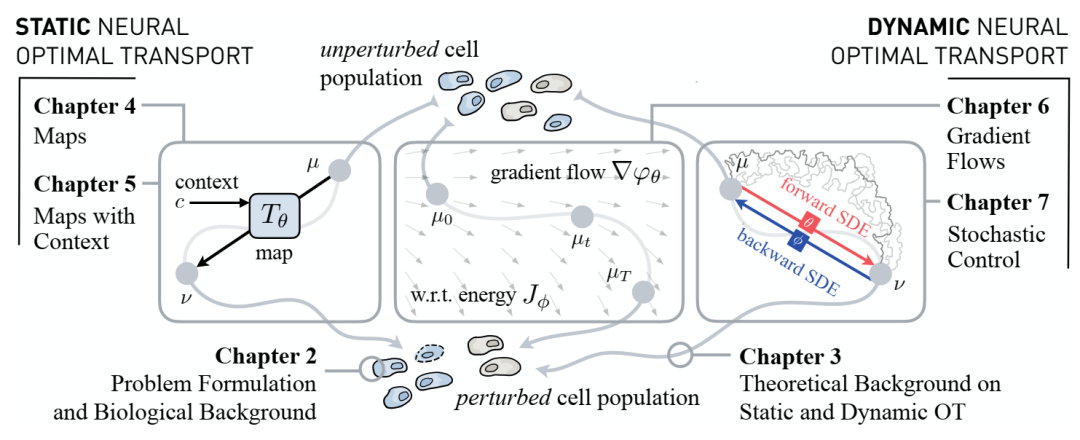
论文的结构以及参考章节

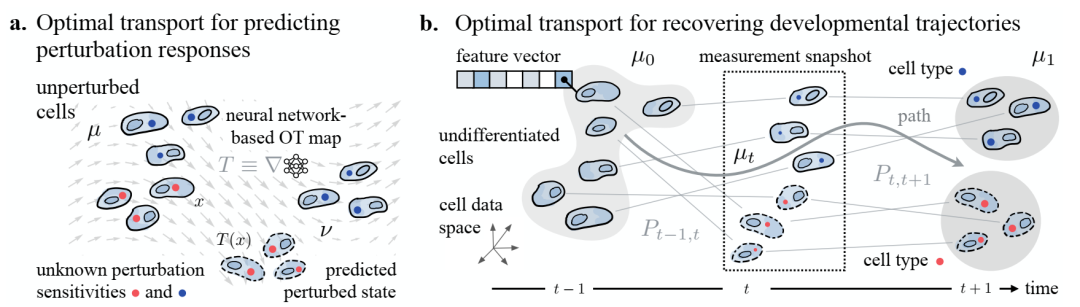生物医学中不同动态过程的概述。 a. 为了理解和预测未受干扰的细胞群 m 对治疗剂等刺激物的反应，我们需要确定一个图 T 来解释其进化为受干扰的细胞群 n。然后，细胞 x 的扰动状态由 T(x) 给出。b. 发育过程描述了通常同质的未分化细胞群进化成各种细胞谱系的过程。从测量快照重建此类过程可以通过描述从 u0 到 u1 的演化的顺序比对 Pt−1,t 来实现，或者通过识别捕获细胞分化过程的总体全局路径来实现

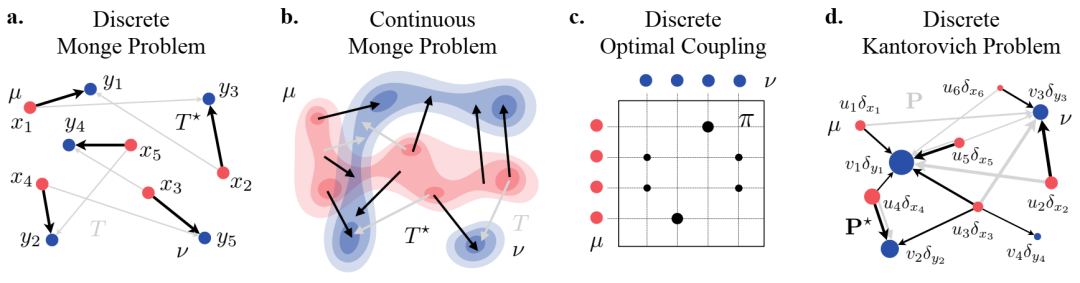离散和连续测量的静态 OT 问题的不同表述的概述。(a) 离散测量和 (b) 连续测量 u、v 的蒙日图。最优映射T？最小化（3.1）。(c) 离散测量u 和 v 的最佳耦合 p (3.2)。d. 最佳传输计划 P 的离散测量 u 和 v 的 Kantorovich 松弛的质量分裂原理？和一个非最优计划 P。

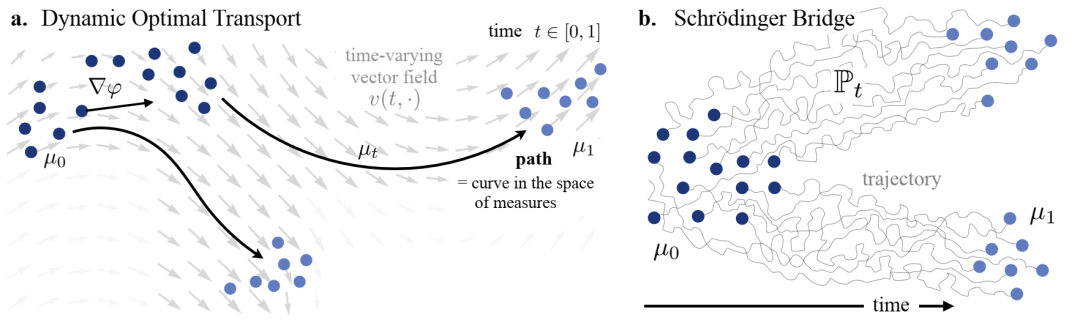
动态 OT 问题的不同表述的概述。 a.  我们可以将测量 ut 随时间的演变建模为时变向量场 v(t,·) 上的最小路径或根据凸势 rj 的梯度。b. 或者，从随机的角度来看，我们可以研究熵正则化 OT 问题 (3.3) 的动态公式，并找到描述从 u0 到 u1 的粒子动力学的随机过程 Pt。

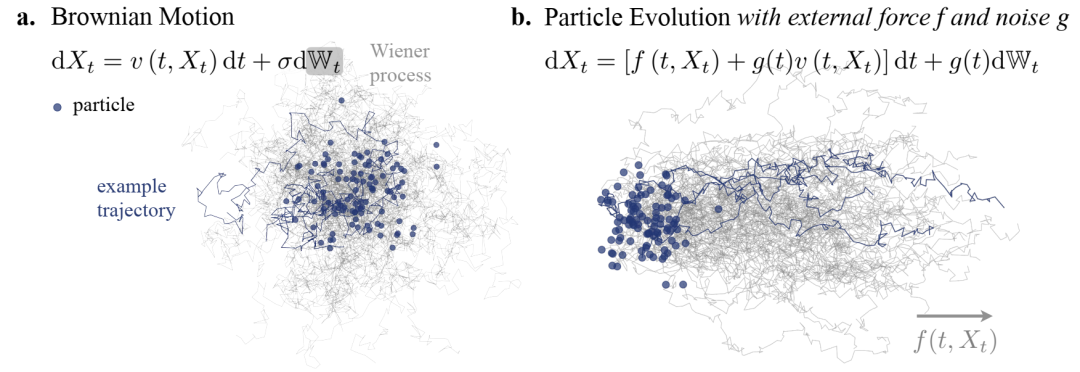不同 SDE 类别的比较。(a) 粒子根据噪声水平 s 在各个方向上按照简单 BM 演化。(b) 具有外部速度 f 的粒子演化，这里通过水平漂移和随时间变化的噪声 g 进行示例。粒子的初始位置用蓝点表示，示例轨迹用蓝线突出显示。

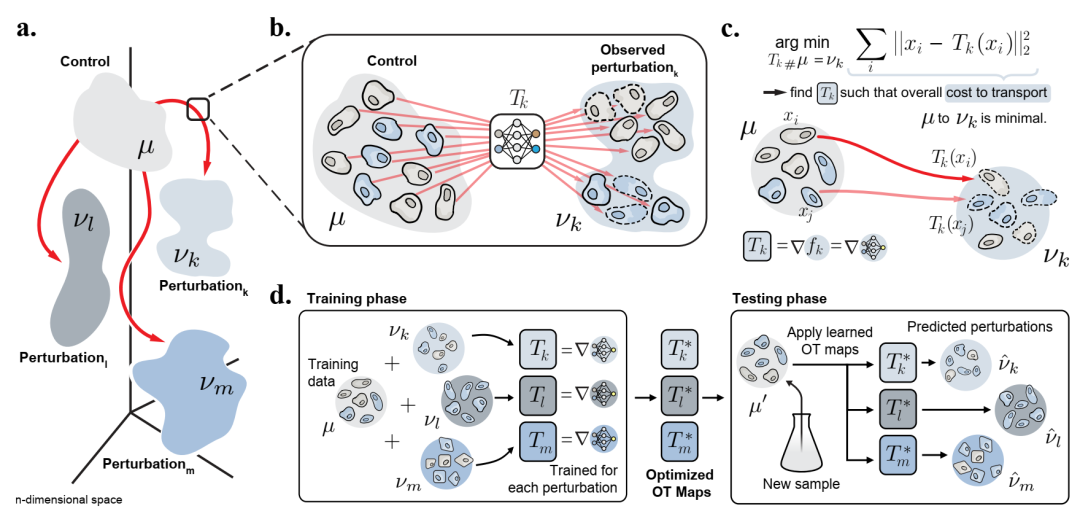CellOT 模型概述。(a) 在未处理的对照状态 (u) 或几种扰动状态之一 (vk、vl、vu、…) 下测量单细胞的分布。这些分布位于轮廓特征的高维空间中。(b) 对于扰动 k，我们的目标是使用函数 Tk 对其进行建模，该函数将 u 中未处理的细胞映射到 vk 中经过处理的对应细胞。(c) 由于缺乏配对测量，我们假设扰动在最小努力原则下将 u 转换为 vk 。特别是，我们使用最优传输理论学习 Tk 来直接估计这种分布映射作为最优传输对偶势 rgq 的梯度。(d) OT 地图是独立学习所有扰动的。因为这些图谱是完全参数化的，所以可以对 CellOT 进行训练，例如，在一组最初提供的样本上进行训练，然后对源自新的、以前未见过的样本的未处理细胞进行预测。

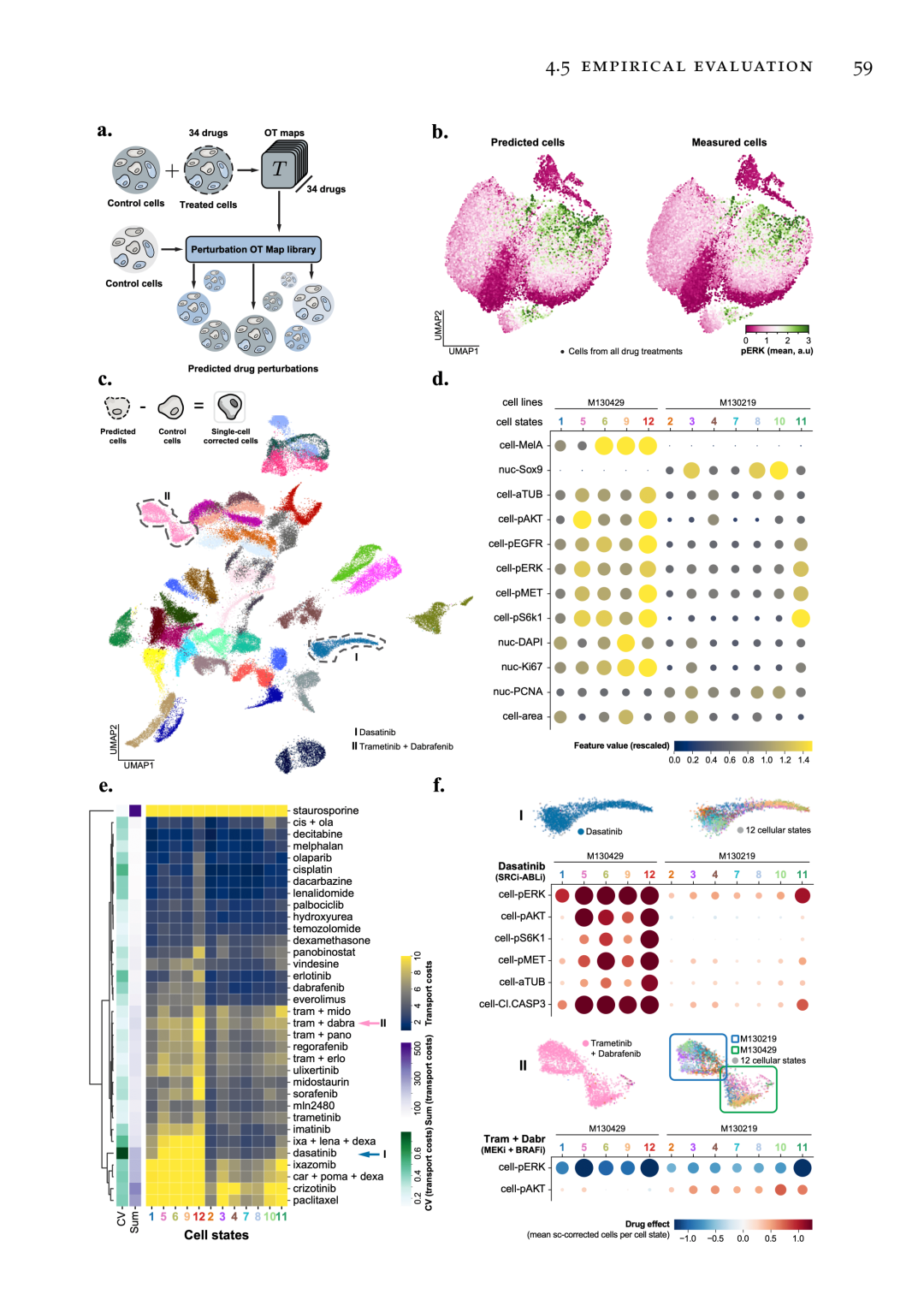CellOT 有助于癌症药物的多重单细胞表征。(a) CellOT 训练和预测设置。训练了 34 个 CellOT 模型，每种药物扰动一个模型。随后，每个模型都用于从一组常见的看不见的对照细胞中预测受到干扰的细胞。(b) UMAP 投影由来自 34 个扰动的相同数量的预测和测量单元构建。点对应于细胞，用颜色编码测量或预测的 pERK 强度，(c) 使用预测细胞对单细胞扰动效应进行 UMAP 投影。点对应于细胞，针对药物治疗进行颜色编码（参见图 A.1，了解单细胞扰动效应计算的完整图例）。(d) 在对照细胞中识别的细胞状态。每列代表一个细胞状态。横轴，细胞状态根据其与细胞系 M130219 和 M130429 的关联进行排序。纵轴，蜂窝特征（完整特征集参见图 A.1）。圆圈的大小和色调根据特征值缩放。(e) 每种细胞状态药物治疗的运输成本 (TC) 聚类图（主热图，蓝黄色配色方案），每种药物所有状态的 TC 总和 (Sum)（热图左侧第一列，紫色） 、每种药物 TC 的变异系数 (CV)（热图左侧第二列，绿色）以及基于药物细胞状态 TC 分层聚类的树状图。细胞状态按 (d) 中的方式排序。（f）细胞状态对药物治疗的特异性反应。上图 (I) 达沙替尼。下图 (II) Trametinib + Dabrafenib。小组组织：（c）中 UMAP 投影的左上角、以条件为中心的放大。右上角，与左上角相同，但针对单元状态分配进行了颜色编码。底部，列代表细胞状态，行突出显示特征。“cell-”代表平均细胞强度。圆圈根据药物作用大小进行缩放，作用越强，圆圈越大。负值以蓝色色调编码，正值以相应圆圈的红色色调编码。

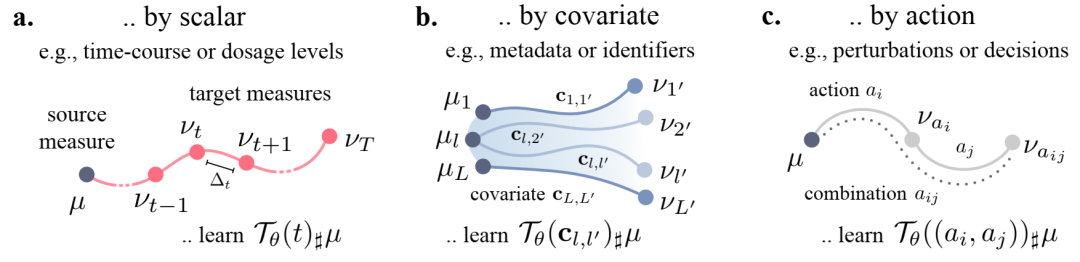从源 u 到目标度量 v 的演变可以取决于各种性质的上下文变量 c。这包括 (a) 标量，例如时间或剂量 t，它们确定最佳传输的大小，(b) 基于存储在向量 cl,l 中的附加信息（u 和 v 之间可能不同）将测量流转入另一个测量，或 (c) 离散和复杂的动作ai，可能是aij的组合。我们寻求一个统一的框架来根据任何类型的条件 c 生成映射 Tq(c)。

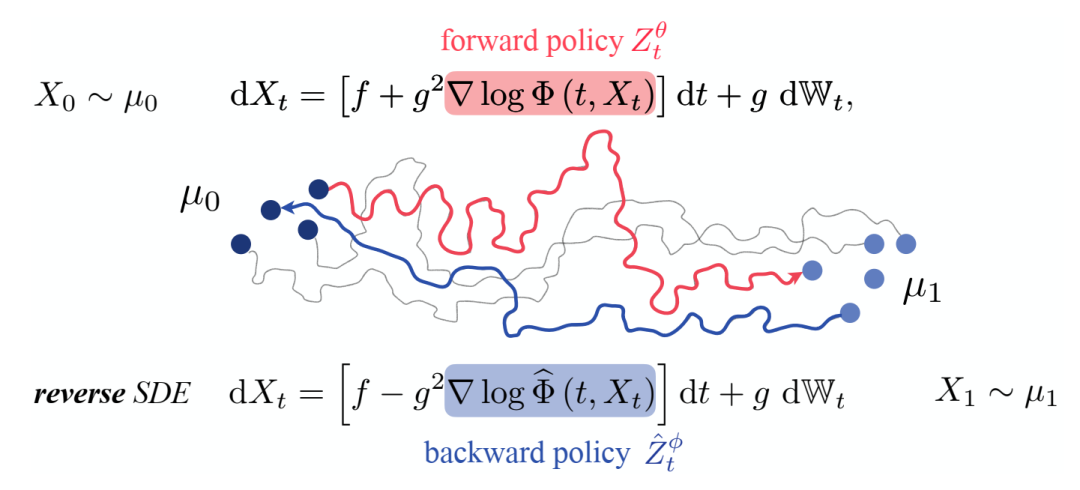扩散薛定谔电桥的参数化。具有前向策略 Zt 的前向 SDE 将粒子 X0 ∼ u0 从 t = 0 引导到 t = 1 时的 u1。反向 SDE 在时间上向后运行。这里，后向策略 Zˆt 决定了粒子 X1 ∼ u1 (t = 1) 到 u0 (t = 0) 的演化

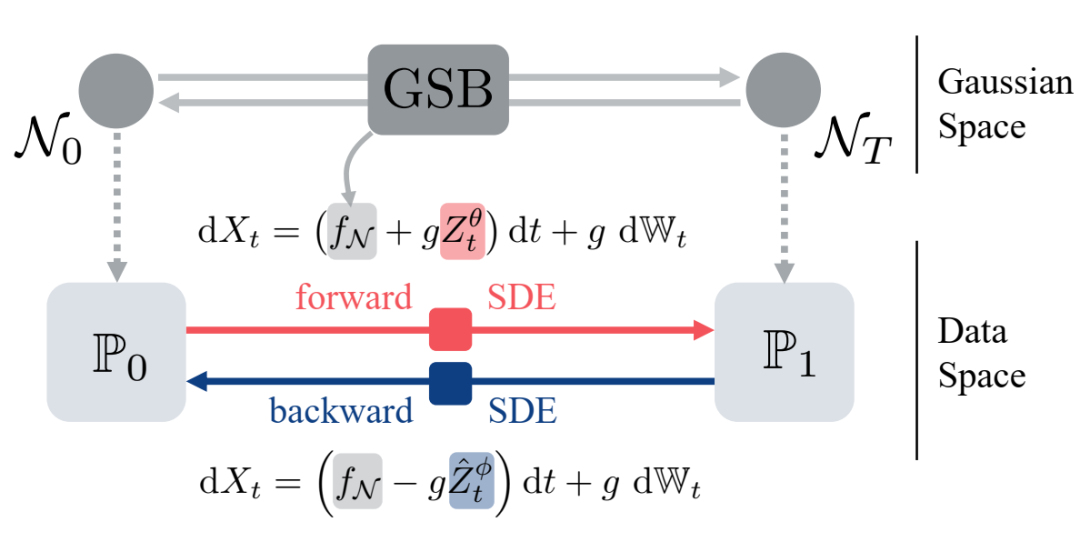解决 u0 和 u1 之间的 SB 问题非常困难，因为它需要学习两个符合所需边际的 SDE 的时间相关漂移，而这些漂移的随机初始化通常远远不能满足该约束。我们提出了一种依赖于数据的过程，该过程首先依赖于数据测量的高斯近似，它提供了（7.31）（GSB）中的封闭形式漂移fN。我们证明这有助于前向/后向漂移 Zˆtq、Zˆtf 的训练。

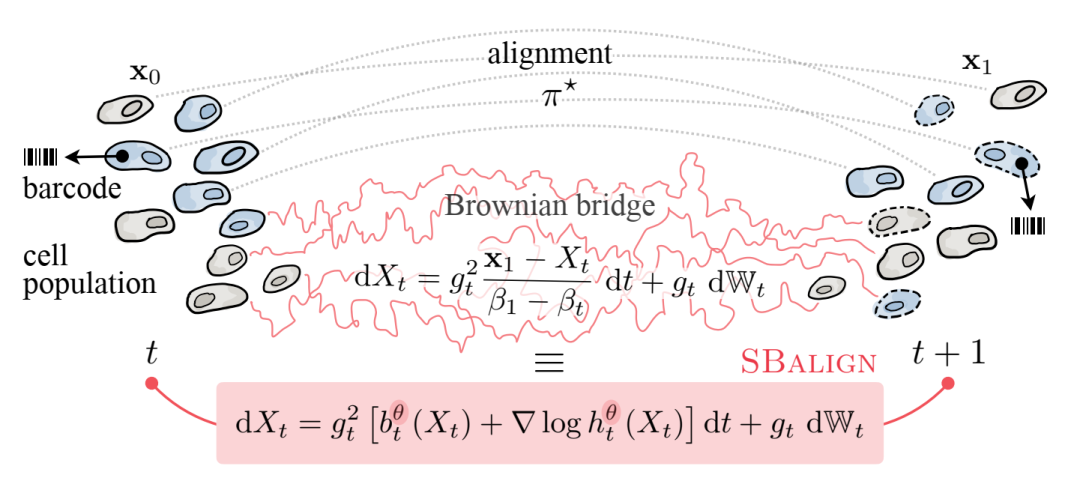SBalign 概述。在细胞分化的背景下，我们的目标是了解群体从 t 时的状态转变为 t + 1 时的进化过程。通过基因标记（即条形码），我们能够追踪时间点 t 的祖细胞进入其后代 t + 1. 这为我们提供了连续时间步长的群体之间的对齐情况。我们的目标是恢复从 x0 到 x1 的随机轨迹。为了实现这一目标，我们将以 x0 和 x1 为条件的 SDE 的表征（利用 Doob 的 h 变换）与 x0 和 x1 之间的布朗电桥（经典薛定谔电桥理论）的表征联系起来，从而实现更简单、方差更低的训练过程 和强有力的实证结果。

微信群                  公众号