
导语
无标度网络是涌现行为最著名的例子之一,其在社会系统中无所不在,特别是在用户可以互相关注的在线社交媒体中。通过使用GPT3.5-turbo作为语言模型,分析多个生成式主体(generative agents)的互动,本文展示了它们不仅能模拟个体人类的语言行为,还能展示出人类社会内在的集体现象,尤其是无标度网络的涌现。结果发现,GPT3.5-turbo的偏斜Token先验分布会干扰这一过程,可能导致网络出现极端集中化的对齐现象。本文展示了如何通过重命名主体来消除这些Token先验,从而使模型能够生成从随机网络到更逼真的无标度网络的各种网络。
研究领域:复杂网络,无标度网络,涌现,大语言模型,对齐现象 Giordano De Marzo, Luciano Pietronero, David Garcia | 作者刘培源 | 译者
Giordano De Marzo, Luciano Pietronero, David Garcia | 作者刘培源 | 译者 论文题目:Emergence of Scale-Free Networks in Social Interactions among Large Language Models论文地址:https://arxiv.org/abs/2312.06619v1
论文题目:Emergence of Scale-Free Networks in Social Interactions among Large Language Models论文地址:https://arxiv.org/abs/2312.06619v1
引言
人工智能(AI)微妙而深远地渗透到我们的日常生活中,尤其是随着深度学习技术的兴起。这种潜移默化的影响随着生成式AI(GenAI)和尤其是大型语言模型(LLMs)如ChatGPT的崛起,显得更为剧烈。这些技术,曾经被视为研究辅助工具,如今已经崭露头角,成为科学探索的工具和焦点。它们超越了初步的编程和写作辅助角色,能够胜任它们未曾被设计或训练过的任务[1]。在这种背景下,大量的关注集中在理解和分析单个模型的能力上[2, 3, 4]。这些研究提供了对大语言模型的微妙功能、偏见和潜在应用的深入洞见[5, 6, 7, 8, 9, 10, 11, 12]。然而,更需要深入探索的领域是多个大语言模型之间的互动[13, 14, 15]。这个研究方向至关重要,尤其是考虑到人类社会交互如何引发涌现的集体行为[16]。
对孤立的大语言模型行为的研究,虽然富有启发性,但对这些模型在更为复杂、交互性的环境中的隐动力学(potential dynamics)只能提供有限的视角。在人类社会中,许多最重要的过程和现象并非单个行为的产物,而是集体行为的结果。例如,文化趋势、经济转变和社会运动,都是众多个体相互作用的涌现性质的体现,通常以复杂且难以预测的方式出现[17]。大语言模型是生成式主体概念的核心部分:将大语言模型与其他结构和属性(如记忆、计划和身份)结合,对人类行为进行建模[18,19]。当多个生成式主体在模拟环境中互动时,它们可能展现出无法预测或并未直接编码在任何单一主体或大语言模型中的行为,以及产生出预料之外的结果[20]。这些情况源于多个主体及其大语言模型之间的复杂相互作用和依赖关系。从某种意义上讲,每个生成式主体都为一种更为复杂且难以预测的集体“智能”或模式做出贡献,这种智能或模式比其个体能力所能暗示的要复杂得多。例如,使用生成式主体进行的模拟显示了信息扩散和协调等涌现行为的实例[18]。
复杂网络是涌现结构的代表性例子[21]。复杂网络拥有无标度(free-scale)的度分布,带有令人惊异的涌现性质:度的方差可能随网络规模的增长而增大,而且疫情的传播可能极其难以应对[22]。例如,万维网和在线社交网络由无数个体的互动形成,其中的关系和信息流动塑造了一个动态的、不断演化的结构。特别是,像Twitter或Instagram这样具有关注者链接的在线社交网络,已被证实具有无标度分布[23, 24]。这些例子凸显了复杂网络的一个关键特性:它们的结构和动力学是其组成部分之间相互作用的涌现产物,而非由控制系统的中央实体所决定。
在本文中,我们首次探讨生成式主体如何自组织形成网络结构,以及这些结构是否可能具有复杂性。正如人类互动催生出社交网络的复杂结构一样,我们推测生成式主体间的交互也能孕育出同等错综复杂的网络。本研究的重要性由两个新兴趋势所凸显:一方面,如Chirper等人工智能驱动的社交网络的兴起,以及预期中传统社交网络中大语言模型控制的机器人数量增加[25, 20];另一方面,使用生成式主体的基于主体模型的发展[15, 14]。这些发展趋势预示着一个由大语言模型塑造的数字生态系统的诞生,其中,人工智能实体间的互动可能将像人类交流一样成为日常。
结果
-
模拟社交网络的生长
我们构建了一个简化版的在线社交网络模型,该模型受到诸如Barabasi-Albert模型[26]等复杂网络生长模型的启发,其中节点依次加入网络并与其他节点建立联系。在我们的模拟中,节点是代表在线社交网络用户的生成式主体。我们并未通过方程式明确地建模和模拟主体的行为,而是利用大语言模型来引导生成式主体的活动。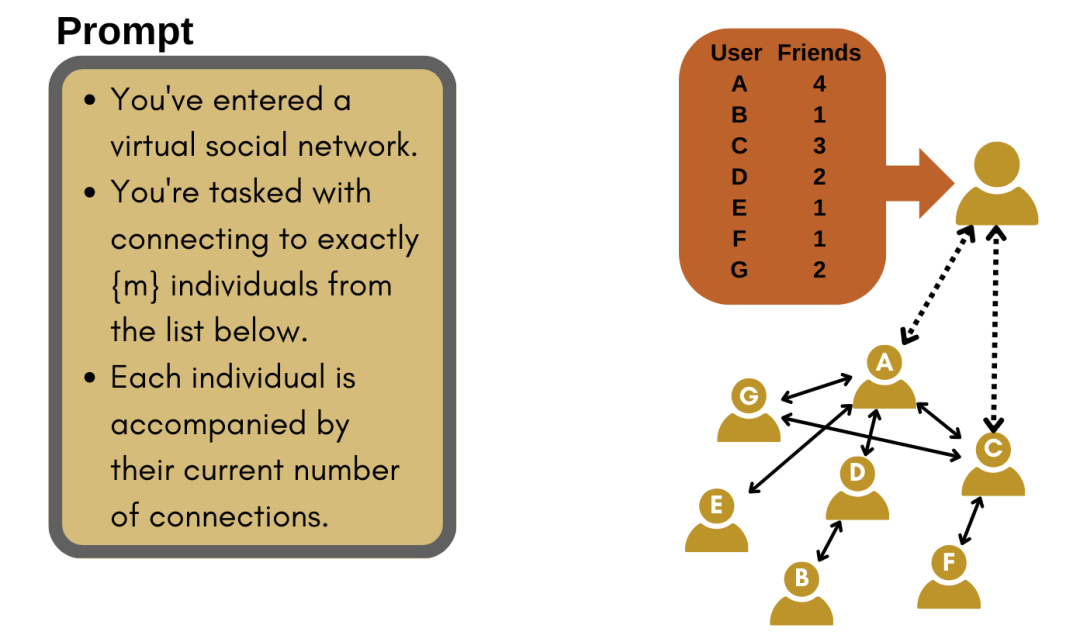
图1:基于大语言模型的生成式主体网络生长。左图:我们用于初始化每个生成式主体的大语言模型,使其作为在线社交网络的用户的提示(promot)。该提示后接一个详尽的列表,列出了所有网络用户及其朋友数。右图:模拟过程的示意图。在每个时间步,新的主体使用给定的提示进行实例化,并接收现有网络用户的度信息。然后,主体确定它希望连接的m个用户,并更新网络以包括这些新的连接。随着新主体的加入,这个迭代过程持续进行。
图1展示了我们的生成式主体在模拟中的行为。在每个时间步中,使用OpenAI API,一个由GPT-3.5-turbo驱动的生成式主体被初始化,使用图1(左图)中显示的提示,这代表一个在线社交网络中的用户,其任务是选择与之建立联系的m个用户。主体接收一个列表,列出了所有现有的其他主体,每个主体由一个随机的3个字符的字符串标识,以及它们已经拥有的连接数量,如图1(右图)所示。用户列表的排序完全随机,并且在每个时间步中会变化,以避免由于在提示中的位置产生潜在的偏见。然后,新的主体通过回复它们的名称自主决定与哪些其他主体建立联系。值得注意的是,在我们的模拟中,主体接收到的信息与Barabasi-Albert模型中节点拥有的信息完全一致。主要的区别在于创建连接的它们:在Barabasi-Albert模型中,节点按照一个固定的概率规则进行连接,而我们的主体则基于大语言模型生成的文本生成要连接的节点列表。一旦生成式主体选择了用户,相应的m条无向连边就形成了,网络的度列表也得到更新。这个过程会反复迭代,直到达到预期的网络规模。
-
网络拓扑
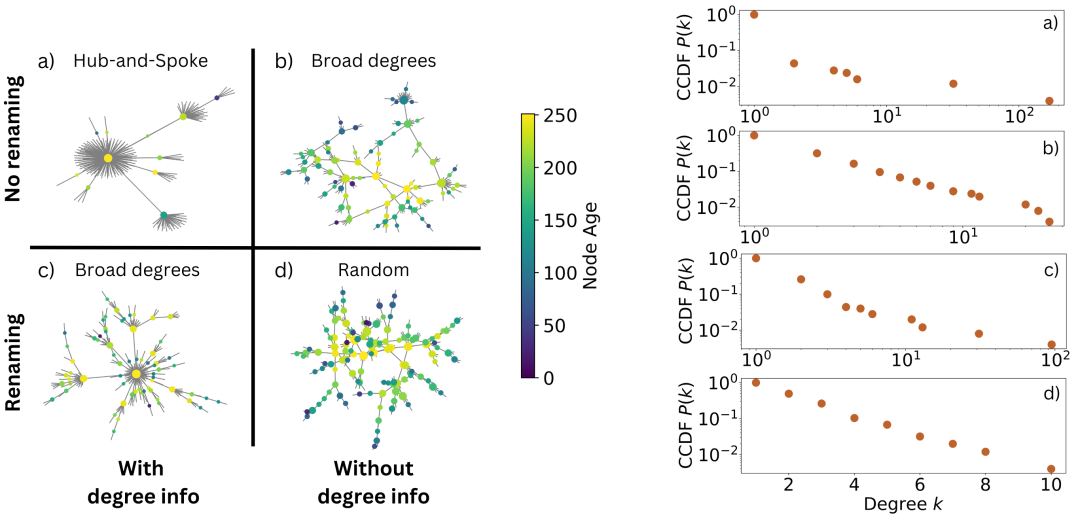
图2:网络拓扑结构。左图:展示了主文中讨论的四种情况对应的不同网络拓扑结构:Token先验的存在/缺失,以及主体界面中度数的存在/缺失。颜色反映了节点的年龄,而节点的大小则与度数的对数成比例。右图:四种不同网络拓扑结构的互补累积分布函数(Complementary Cumulative Distribution Functions,CCDF)。
在确定了网络生长过程后,我们将重点分析所得网络的结构。当主体能看到其他人的朋友数量时,生成的网络呈现出中心-辐射的拓扑结构,其中极少数的主体获得了绝大部分的连边,如图2.a左侧面板所示。在这种情况下,新节点的传入连接仅限于少数之前的节点,导致了度的不均衡,这比实际社交网络结构中所观察到的差异更大。这种极端的集中现象可以在图2右侧面板上的CCDF中看到。这是一种人工智能对齐方式,导致网络结构不真实和网络度数极端集中。
为了更深入理解这个网络生成过程,我们调整了模型,移除了向主体展示的度信息,也就是说,每个节点的朋友数量不会显示在主体看到的界面上,它们只会收到其他主体的名称列表以供选择。如果按照Barabasi-Albert模型进行类比,我们会预期这将生成一个随机网络结构。然而,这种没有节点度信息的模拟却出人意料地产生了一个具有更广泛度分布的网络,从拓扑上看,它更接近实际的在线社交网络,如图2b的左右面板所示。对这个网络拓扑的深入探查揭示了其主要问题:节点存在时长与节点的度并无关联,新节点可能会吸引到不成比例的大度,这在具有优先连接的网络生长模型中并不成立。这个出乎意料的结果可以与大语言模型的Token生成过程中存在的非平凡先验相联系。我们网络中的每个主体都被赋予一个随机名称,而大语言模型则对某些字母序列有偏好,这可能受到其训练语料库中字母频率的影响。这可能是当使用字母时的Zipf定律或使用数字时的Benford定律的体现[27, 28, 29]。这种偏好使得某些主体仅因其名称在大语言模型中的先验频率较高,而获得了更高的人气和更多的连接。因此,我们观察到的广泛分布是GPT3.5-turbo响应中固有偏见的结果,而非我们模拟中生成式主体所复现的优先连接模型的结果。
为了验证对GPT3.5-turbo先验概率影响结果的怀疑,我们通过在每次迭代时都随机更改主体的名称来调整模拟,只是简单地置换它们的名称,但保留它们在网络中的连接,从而也追踪了它们的度信息。这种带有重命名的模型版本,结合主体界面中的节点度信息,能够生成一个与实际网络相似的复杂网络结构,如图2,c的左侧面板所示。在检查节点的存在时间时,该网络展现出节点存在时间与度数之间的典型相关性,更接近优先连接过程所产生的结果。如果我们改变界面以隐藏节点度数信息,同时保持重命名,那么结果就类似于一个随机网络,如图2,d的左侧面板所示,右侧面板显示了一个狭窄的度分布(注意线性水平轴)。因此,通过在界面中重命名主体后,该模型从拥有度信息的复杂网络结构,变为无法访问其他主体度数的随机网络结构。基于此,未经重命名且拥有度信息的模型的中心-辐射结构是两种集中过程的结合:一种是优先连接,另一种是Token名称的先验,这导致了一个极度中心化的网络。
-
无标度网络
如上所述,当通过改名消除Token先验时,我们发现,只要主体能看到其他主体的朋友数量,网络结构就会从随机网络转变为更复杂的形态。而在未进行改名的情况下,只要主体能看到其他主体的朋友数量,网络就会呈现出中心枢纽与辐射状的拓扑结构。这些现象可以通过考虑Barabasi-Albert模型[26]的不同模式来理解,其中,与特定节点建立连接的可能性与其度数k成正比,这种关系可以通过连接概率π(k)来表示。
π(k) ∼ kμ
这种机制被称为“优先连接”,也就是说,度数较高的节点更有可能获取新的连接。其中,连接指数μ在塑造网络拓扑结构上发挥了决定性的作用[30]:
-
当μ=0时,网络是具有指数度分布的随机网络。
-
当0<μ<1时,网络呈现出一个拉伸指数的度分布。
-
当μ=1时,网络变为无标度网络,其度分布特征表现为幂律分布。
- 当μ>1时,网络演变为中心枢纽与辐射状的结构,通常被形象地描述为“富者愈富”的场景。
典型的在线社交网络,具有与线性优先连接相对应的度分布。偏离这一狭窄区间的值,将会导致明显不同的分布。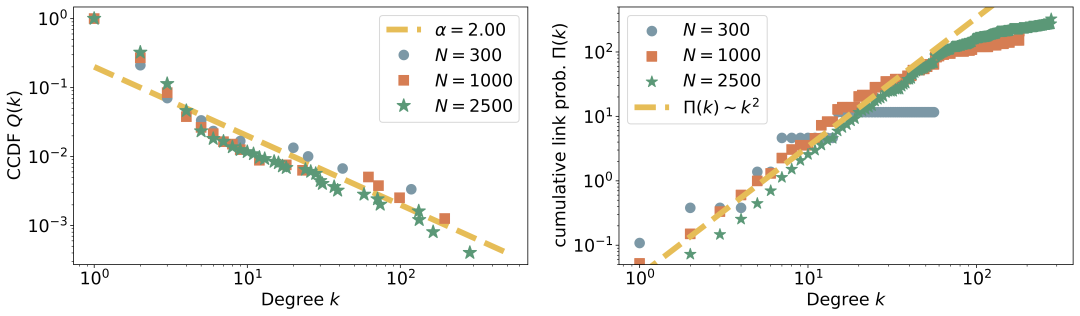
图3:线性优先连接。左图:三个网络规模N=300、1000、2500的度的互补累积分布函数。实线为观察指引,对应于指数α=2的幂律概率密度函数。网络展现出无标度特性。右图:三个网络快照的重构累积连接概率Pi(k)作为k的函数。随着节点数N的增加,出现了更长的二次函数曲线区域。这对应于无标度网络和人类互动中典型的线性优先连接。
我们的生成式主体模型反映了在Barabasi-Albert模型中所观察到的规律,即当优先连接指数μ大于零时,度分布从指数型逐渐演化为更广泛的概率分布,最终在μ>1的情况下,形成富者愈富的局面。我们的目标是确定由我们的生成式主体产生的网络归属于哪种模式(拉伸指数随机网络、无标度网络,或中心-辐射网络)。图3(左)展示了随着网络增长至N=2000个节点,节点度的互补累积分布函数的演变情况。在双对数坐标中,互补累积分布函数的线性趋势表明了无标度的拓扑结构。图中的实线代表了对互补累积分布函数的最大似然拟合[31, 32],对应于一个指数α=1.93±0.12的幂律度分布。
我们的研究发现,生成式主体在在线互动中,如同人类一样,更倾向于自发地形成无标度网络。然而,由于网络规模的相对有限性以及模拟更大网络所需的成本,我们需要进行更深入的分析以确认生成式主体是否真的展示出了线性优先连接的特性。我们重构了连接概率π(k);如果这个概率与度数k呈线性关系,那么这就暗示着网络是由线性优先连接机制控制的无标度网络。我们采用了[33]中概述的方法,检查连续的网络快照,计算新节点连接到具有特定度数的现有节点的可能性,从而得出π(k)。为了减少噪声,我们计算了累积连接概率Π(k)=∑kiπ(k)并将其绘制为k的函数。在存在线性优先连接的情况下,这个累积指标呈现二次函数增长。图3(右)展示了上述三种网络规模的Π(k)。这些图表揭示了,随着N的增长,二次函数形状越来越显著,这表明生成式主体之间存在线性优先连接。
讨论
大语言模型已经在模拟人类语言方面展示出了娴熟的技巧,其生成的文本往往与人类创作的作品无法区分。这种能力激发了人们对利用大语言模型构建新一代基于主体的模型(ABMs)的兴趣,从而实现前所未有的真实感[15]。在这其中,主体甚至可以作为社交媒体用户的数字孪生。这样的进步在从测试社交平台干预[14]到分析疫情传播[34]等各种应用中都蕴藏着巨大的潜力。然而,要实现这种潜力,关键在于理解大语言模型不仅能够在个体层面复制人类行为,而且能够展现出对人类社会至关重要的集体行为。由于大部分大语言模型的基准测试都是围绕着问答任务的,因此,对大语言模型在许多个体与环境互动并相互作用的集体中展现出的群体行为的理解尚有限。
在本研究中,我们聚焦于人类互动中的一种基本涌现模式——无标度网络,来探讨这个问题。这类网络在从生物到社会经济各领域的多种系统中都普遍存在,其拓扑特性表现为度分布遵循幂律,因此大部分节点的连接较少,而少数节点的连接极多。我们的研究发现,由GPT3.5-Turbo驱动的生成式主体模型(即ChatGPT所使用的大语言模型)在其度分布的无标度特性上,与在线社交网络中的人类行为相似。生成式主体的网络展现出相似的线性优先连接倾向,从而形成无标度网络。值得注意的是,我们模拟生成的无标度网络的幂律指数接近于-2,即著名的Zipf定律[27, 29]。这个值与Twitter等在线社交网络观察到的数值非常接近[24]。
总体而言,我们的研究结果强调了将大语言模型作为生成式主体的挑战。大语言模型通常被形象地描述为“随机鹦鹉”(stochastic parrot)[35],一般认为它们是根据前文来随机生成句子后续词汇的系统。然而,我们的研究发现,大语言模型能够捕捉到超越纯文本生成的人类行为特征,这通常是标准基准测试的主要关注点。与基于单一回应评估的方法相比,我们的方法涉及到对整个回应分布的比较。我们展示了在类似的情境中,人类和生成式主体表现出相似的连接概率分布。这一观察对基于蒙特卡洛抽样的基于主体的模型至关重要,因为它们需要对每个主体进行多次更新,以探索所有可能的回应范围。因此,要成功地将大语言模型整合进基于主体的模型,我们必须确保这些模型不仅能在特定情况下复制出真实的类人反应,还能准确地代表主体相互作用情境下,潜在人类行为的整体概率分布。
参考文献
[1] S. Bubeck, V. Chandrasekaran, R. Eldan, J. Gehrke,E. Horvitz, E. Kamar, P. Lee, Y. T. Lee, Y. Li, S. Lundberg, et al., Sparks of artificial general intelligence: Early experiments with gpt-4, arXiv preprint arXiv:2303.12712(2023).[2] Y. Chang, X. Wang, J. Wang, Y. Wu, K. Zhu, H. Chen, L. Yang, X. Yi, C. Wang, Y. Wang, et al., A survey on evaluation of large language models, arXiv preprint arXiv:2307.03109 (2023).[3] F. F. Xu, U. Alon, G. Neubig, and V. J. Hellendoorn, A systematic evaluation of large language models of code, in Proceedings of the 6th ACM SIGPLAN International Symposium on Machine Programming (2022) pp. 1–10.[4] K. Valmeekam, A. Olmo, S. Sreedharan, and S. Kambhampati, Large language models still can’t plan (a benchmark for llms on planning and reasoning about change), arXiv preprint arXiv:2206.10498 (2022).[5] L. P. Argyle, C. A. Bail, E. C. Busby, J. R. Gubler, T. Howe, C. Rytting, T. Sorensen, and D. Wingate, Leveraging ai for democratic discourse: Chat interventions can improve online political conversations at scale, Proceedings of the National Academy of Sciences 120, e2311627120(2023).[6] B. J. Jansen, S.-g. Jung, and J. Salminen, Employing large language models in survey research, Natural Language Processing Journal 4, 100020 (2023).[7] J. S. Park, L. Popowski, C. Cai, M. R. Morris, P. Liang, and M. S. Bernstein, Social simulacra: Creating populated prototypes for social computing systems, in Proceedings of the 35th Annual ACM Symposium on User Interface Software and Technology (2022) pp. 1–18.[8] A. J. Thirunavukarasu, D. S. J. Ting, K. Elangovan, L. Gutierrez, T. F. Tan, and D. S. W. Ting, Large language models in medicine, Nature medicine 29, 1930 (2023).[9] M. Abdulhai, G. Serapio-Garcia, C. Crepy, D. Valter, J. Canny, and N. Jaques, Moral foundations of large language models, arXiv preprint arXiv:2310.15337 (2023).[10] K. Singhal, S. Azizi, T. Tu, S. S. Mahdavi, J. Wei, H. W. Chung, N. Scales, A. Tanwani, H. Cole-Lewis, S. Pfohl, et al., Large language models encode clinical knowledge, Nature 620, 172 (2023).[11] M. C. Frank, Baby steps in evaluating the capacities of large language models, Nature Reviews Psychology 2, 451 (2023).[12] T. Webb, K. J. Holyoak, and H. Lu, Emergent analogical reasoning in large language models, Nature Human Behaviour 7, 1526 (2023).[13] G. Betz, Natural-language multi-agent simulations of argumentative opinion dynamics, Journal of Artificial Societies and Social Simulation 25 (2022).[14] P. T¨ornberg, D. Valeeva, J. Uitermark, and C. Bail, Simulating social media using large language models to evaluate alternative news feed algorithms, arXiv preprint arXiv:2310.05984 (2023).[15] I. Grossmann, M. Feinberg, D. C. Parker, N. A. Christakis, P. E. Tetlock, and W. A. Cunningham, Ai and the transformation of social science research, Science 380, 1108 (2023).[16] D. Garcia, M. Galesic, and H. Olsson, The psychology of collectives, Perspectives on Psychological Science, 17456916231201139 (2023).[17] P. W. Anderson, More is different: Broken symmetry and the nature of the hierarchical structure of science., Science 177, 393 (1972).[18] J. S. Park, J. O’Brien, C. J. Cai, M. R. Morris, P. Liang, and M. S. Bernstein, Generative agents: Interactive simulacra of human behavior, in Proceedings of the 36th Annual ACM Symposium on User Interface Software and Technology (2023) pp. 1–22.[19] H. Zhang, W. Du, J. Shan, Q. Zhou, Y. Du, J. B. Tenenbaum, T. Shu, and C. Gan, Building cooperative embodied agents modularly with large language models, arXiv preprint arXiv:2307.02485 (2023).[20] J. He, F. Wallis, and S. Rathje, Homophily in an artificial social network of agents powered by large language models(2023).[21] A. Capocci, V. D. Servedio, F. Colaiori, L. S. Buriol, D. Donato, S. Leonardi, and G. Caldarelli, Preferential attachment in the growth of social networks: The internet encyclopedia wikipedia, Physical review E 74, 036116 (2006).[22] R. Pastor-Satorras and A. Vespignani, Epidemic spreading in scale-free networks, Physical review letters 86, 3200(2001).[23] S.-Y. Teng, M.-Y. Yeh, and K.-T. Chuang, Toward understanding the mobile social properties: an analysis on instagram photo-sharing network, in Proceedings of the 2015 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining 2015 (2015) pp. 266–269.[24] S. Aparicio, J. Villaz´on-Terrazas, and G. Alvarez, A model ´for scale-free networks: application to twitter, Entropy 17,5848 (2015).[25] J. Luo, Analyzing character and consciousness in aigenerated social content: A case study of chirper, the ai social network, arXiv preprint arXiv:2309.08614 (2023).[26] A.-L. Barab´asi and R. Albert, Emergence of scaling in random networks, science 286, 509 (1999).[27] G. K. Zipf, Human behavior and the principle of least effort:An introduction to human ecology (Ravenio Books, 2016).[28] L. Pietronero, E. Tosatti, V. Tosatti, and A. Vespignani, Explaining the uneven distribution of numbers in nature:the laws of benford and zipf, Physica A: Statistical Mechanics and its Applications 293, 297 (2001).[29] G. De Marzo, A. Gabrielli, A. Zaccaria, and L. Pietronero, Dynamical approach to zipf’s law, Physical Review Research 3, 013084 (2021).[30] S. N. Dorogovtsev, J. F. F. Mendes, and A. N. Samukhin, Structure of growing networks with preferential linking, Physical review letters 85, 4633 (2000).[31] A. Clauset, C. R. Shalizi, and M. E. Newman, Powerlaw distributions in empirical data, SIAM review 51, 661(2009).[32] J. Alstott, E. Bullmore, and D. Plenz, powerlaw: a python package for analysis of heavy-tailed distributions, PloS one 9, e85777 (2014).[33] M. E. Newman, Clustering and preferential attachment in growing networks, Physical review E 64, 025102 (2001).[34] R. Williams, N. Hosseinichimeh, A. Majumdar, and N. Ghaffarzadegan, Epidemic modeling with generative agents, arXiv preprint arXiv:2307.04986 (2023).[35] E. M. Bender, T. Gebru, A. McMillan-Major, and S. Shmitchell, On the dangers of stochastic parrots: Can language models be too big?, in Proceedings of the 2021 ACM conference on fairness, accountability, and transparency (2021) pp. 610–623.
(参考文献可上下滑动查看)
AI+Science 读书会
AI+Science 是近年兴起的将人工智能和科学相结合的一种趋势。一方面是 AI for Science,机器学习和其他 AI 技术可以用来解决科学研究中的问题,从预测天气和蛋白质结构,到模拟星系碰撞、设计优化核聚变反应堆,甚至像科学家一样进行科学发现,被称为科学发现的“第五范式”。另一方面是 Science for AI,科学尤其是物理学中的规律和思想启发机器学习理论,为人工智能的发展提供全新的视角和方法。集智俱乐部联合斯坦福大学计算机科学系博士后研究员吴泰霖(Jure Leskovec 教授指导)、哈佛量子计划研究员扈鸿业、麻省理工学院物理系博士生刘子鸣(Max Tegmark 教授指导),共同发起以“AI+Science”为主题的读书会,探讨该领域的重要问题,共学共研相关文献。欢迎对探索这个激动人心的前沿领域有兴趣的朋友报名参与。 详情请见:人工智能和科学发现相互赋能的新范式:AI+Science 读书会启动
详情请见:人工智能和科学发现相互赋能的新范式:AI+Science 读书会启动
网络科学集智课堂
从现实社会的关系网到虚拟的互联网,从线下到线上,我们的生活始终没有脱离复杂网络。真实的复杂网络从其诞生开始就不断地演化着。网络节点不断地增加,节点之间的连接不断地增长。然而,复杂网络的形成机制是什么?具有什么样的演化规律?它们的演化机制对网络的功能和动力学行为有什么影响?为了回答这些问题,科学家们对复杂网络的探索从未停止。
网络科学是一个蓬勃发展的崭新交叉学科,可以看做复杂系统的骨架,核心是研究各种大型复杂网络之间的共性和处理它们的普适方法,其研究对于发展复杂系统的基本理论及构建产生了极大的推动作用。集智学园目前已经打造了三期网络科学课程:
第一期我们有幸邀请了汪小帆、赵海兴、许小可、史定华、陈清华、张江、狄增如、陈关荣、樊瑛、刘宗华这十个来自六大不同高校、在网络科学领域耕耘多年的教授作为导师,一起探索复杂网络权威巴拉巴西的重磅之作《巴拉巴西网络科学》,共同揭秘网络科学的底层原理。详情请见:与网络科学家一起,“集智”学习《巴拉巴西网络科学》
第二期集智学园特邀陈关荣、项林英、樊瑛、宣琦、李翔、史定华、李聪、荣智海、周进、王琳等网络科学专家作为导师,依托汪小帆、李翔、陈关荣的经典教材《网络科学导论》,开展系列上线课程,以网络动力学为主线构建网络科学知识体系。详情请见:2021重磅新课:探索网络动力学——网络科学第二期
第三期集智学园特邀陈关荣、樊瑛、周进、李翔、张江、闫小勇、刘宗华、石川、虞文武、赵海兴、史定华加入,围绕复杂网络的数学建模与应用进行多角度的介绍。详情请见:从数学建模到多学科应用——网络科学·集智课堂全新升级
1. 粗看长尾,细辨幂律:跨世纪的无标度网络研究纷争史2. 集体智能如何增强人工智能?未来智能社会一瞥3. 集体心智:社会网络拓扑塑造集体认知4. 张江:第三代人工智能技术基础——从可微分编程到因果推理 | 集智学园全新课程5. 加入集智学园VIP,一次性获取集智平台所有内容资源6. 加入集智,一起复杂!
点击“阅读原文”,加入课程




 ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง
ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง







