Nat. Mach. Intell. 速递：超越无限宽度限制的贝叶斯深度神经网络的统计力学框架

关键词：深度神经网络，统计物理，机器学习可解释性

论文题目：A statistical mechanics framework for Bayesian deep neural networks beyond the infinite-width limit论文来源：Nature Machine Intelligence论文地址：https://www.nature.com/articles/s42256-023-00767-6斑图地址：https://pattern.swarma.org/paper/946de568-9df9-11ee-bc79-0242ac17000e

在计算技术进步的推动以及数十年研究的铺垫下，深度学习的发展超过了研究者为之构建坚实理论基础的解释能力。多个研究团队长期努力在基础层面上填补我们理解深度学习的空白。统计物理在这方面取得了深远的成果，并且仍然是一个新的视角和突破的源泉。

尽管深度神经网络在实践中取得了成功，但目前缺乏一个全面的理论框架，可以从训练数据的知识中预测实际相关的分数，如测试准确度。在无限宽度的极限下，每个隐藏层中的单位数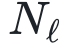（其中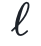=1，…，L，其中L为网络的深度）远远超过训练示例数P，因此会出现巨大的简化。然而，这种理想化与深度学习实践的现实明显不符。该研究使用统计力学的工具集来克服这些限制，并推导出完全连接的深度神经结构的近似配分函数，它编码了有关训练模型的信息。该计算在热力学极限下进行，其中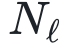和P都很大，它们的比率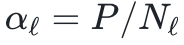则是有限的。这一进展使我们获得：（1）一个针对具有有限α1的单隐藏层网络的回归任务相关的泛化误差的闭合公式；（2）深度架构的配分函数的近似表达式（通过一个依赖有限数量序参量的有效作用），以及（3）深度神经网络在比例渐近极限下与学生t过程（Student’s t-processes）之间的联系。

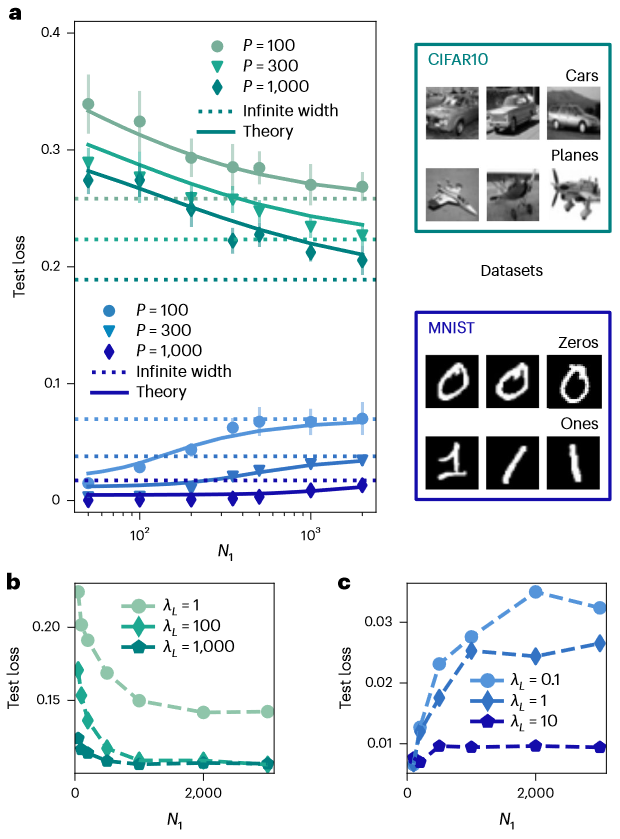
图1. 1HL网络的学习曲线。通过方程进行有限宽度1HL(one-hidden-layer)结构的泛化误差的可测试预测。a，基于Erf激活函数的1HL架构的学习曲线，测试误差随隐藏层尺寸N1变化。在不同训练集大小P上进行实验测试损失（带有误差条表示一个标准差）与从方程1计算得出的理论进行比较（实线）。b、c，最后一层的高斯先验λ1的不同值下的测试误差随N1的变化曲线。其中，误差条在点内，虚线用于引导观察（图2、3同）。网络在来自CIFAR10数据集的P=3,000个示例（b）和MNIST的P=500个示例（c）上进行训练。检查了理论在零温度下的两个定性预测：（1）当λ1增加时，泛化损失应该对任何N1都减小；（2）在大λ1极限下，学习曲线对N1的依赖性消失，是因为此时偏置是常数。

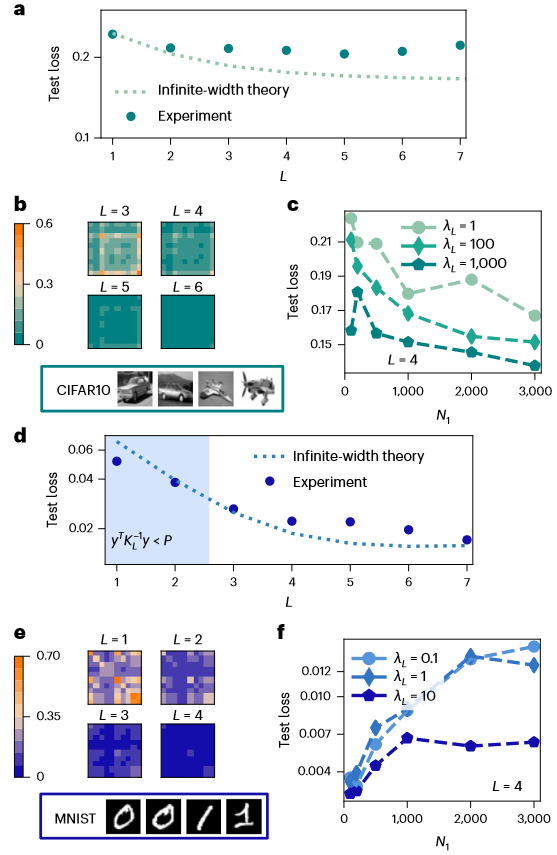
图2 深度网络(L>1)的实验。a,d，采用ReLU激活函数的接近无限宽度和小α（α=0.1）情况下训练于CIFAR10和MNIST上的深度为L的LHL神经网络的测试损失，其中P=100（a对应CIFAR10结果，d对应MNIST结果）。有限宽度的网络只能在SL<1（阴影区域，即只能在MNIST任务和深度L<3。其中，可观测标量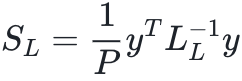。）时优于无限宽度的预测。b,e，可视化网络不断迭代后的无限宽度NNGP核在不同层的条目（b对应CIFAR10，e对应MNIST）。ReLU NNGP核在不断迭代后趋于零，导致了特征值几乎消失，使得SL最终总是大于1。c,f，基于P=1,000个示例训练的4HL网络的测试损失，不同正则化强度的情况（其中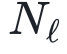=N=1000；c对应CIFAR10，f对应MNIST）。尽管增加最后一层高斯先验的大小仍然改善了所有N的泛化性能，但不再像1HL网络那样清晰，在大λL情况下，曲线随N变化不再是一个常数。

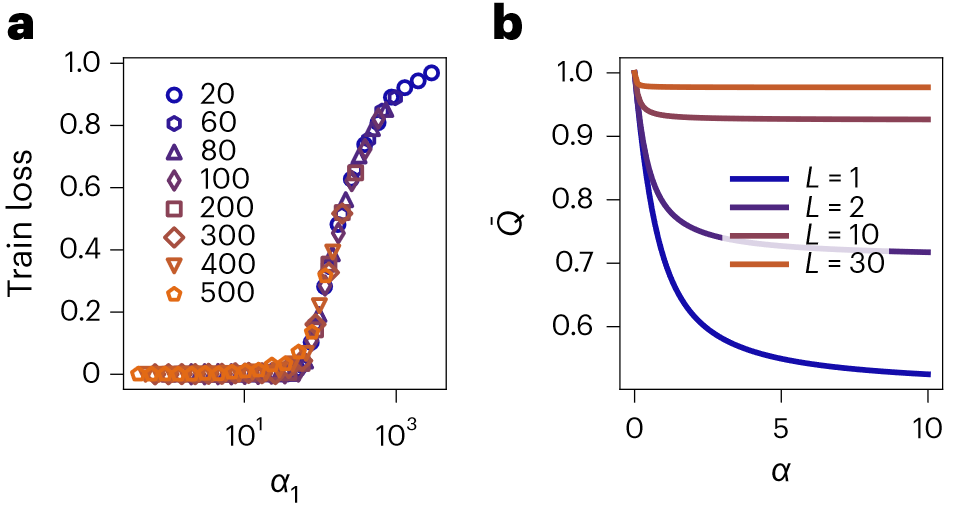
图3. 随着深度L的增加，随机数据和序参量的普遍行为。a，不同1HL架构在完全随机任务上随α1变化的训练损失（即输入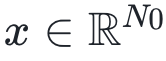，其中N0 = 5和标量输出y都是从均值为零、方差为单位的正态分布中采样独立同分布的随机变量）。其中，误差条在数据点内。目前本文理论只描述了训练误差恰好为零的过参数化极限，而无法解释这种普遍现象。b，采用ReLU激活函数在各向同性网络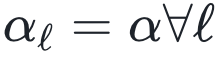情况下，对于不同的深度L对解(在零温度极限下的鞍点方程的精确解)进行数值评估。随着L的增长（L≈30），对所有的α来说，序参量迅速趋近于1。这表明在渐进区域中，DNNs也会在在P，N之后深度L趋于无穷时收敛到一个核心限制

编译｜余孟君

神经网络的统计力学课程

课程详情：

黄海平：神经网络的统计力学课程 | 50人免费名额

推荐阅读

‍1. 深度神经网络的统计物理：寻找最优初始化理论2. PNAS速递：深度神经网络预测小尺度湍流动力学3. PNAS速递：基于相似加权交叉学习的深度神经网络和大脑学习4. 张江：第三代人工智能技术基础——从可微分编程到因果推理 | 集智学园全新课程5. 加入集智学园VIP，一次性获取集智平台所有内容资源6. 加入集智，一起复杂！

点击“阅读原文”，加入课程