小寒 | 生命与规则的结合

在探索自然界的奥秘时，我们常常会被其无穷的复杂程度所吸引。下图便是一个例子，它来自于一种软体动物“锥螺”（Conus），其色彩斑斓的壳体上刻画着一些奇妙的几何图案。然而，一个惊人的事实是，这样看似杂乱无章的图案的背后，有可能仅仅源自于一些简单的规则。在了解完一个简单的计算模型后，任何人都可以轻松地复刻乃至创造出类似的图案来。这便是我们今天的主角——元胞自动机（Cellular Automata，以下简称为 CA）。

元胞自动机

用通俗的语言来说，一个 CA 包含一个格子棋盘，有限种类的棋子，以及一个关于棋子行动的规则，这个规则描述了在下一回合，每个格子中的棋子如何根据当前回合的棋盘局面进行变化，通常而言每个格子只会受到其周围邻近格子的影响。

以形式化的语言，CA 的主要组成部分包括：

1. 元胞空间  ，一般是个规则的网格，可以有多种维度。我们把每一个网格称为一个元胞。

2. 状态集合  ，包含了元胞的所有可能状态。

3. 邻域  ，表明每个元胞  受到影响的范围，通常有冯·诺伊曼邻域（上下左右四个邻居）和“摩尔邻域”（周围八个邻居），为了方便起见，我们认为元胞本身也在其邻域中。

4. 转移规则  ，假设元胞在时刻  的状态向量为  。那么元胞  在下一时刻  的状态为  ，完全由上一时刻  其邻域的状态确定。

5. 初始状态  ，我们需要为系统设定一个初始状态，接下来这个系统会一步一步地自动进行演化。

之所以称其为计算模型，是因为我们可以通过设定转移规则和初始状态来模拟计算的过程。这样的计算模型不同于采用冯·诺依曼（von Neumann）式架构的现代的计算机，因此也被称为非冯·诺依曼式架构，尽管它们同样都是冯·诺依曼提出的。看似 CA 只是一个简单的过程，但可以证明某些 CA 与现代计算机一样具有强大的计算能力，专业术语也就是图灵完备的。在精心设计的规则下，CA 能够展现出一些有趣的行为，尤其是在规则本身具有一些物理意义的时候。

规则决定生命

以最为有名的康威生命游戏（Conway’s Game of Life）[1]为例，在这个游戏中，棋盘是一个二维的格子世界，每个格子都对应着一个细胞，只有两个状态：生和死。一个细胞在下一时刻的生死取决于相邻八个格子的情况：

• 繁殖：任何没有细胞的格子，如果周围细胞存活数为3个，将会在这个格子产生新的细胞。

• 存活：如果一个活细胞周围有两个或三个活细胞，它在下一个时刻保持存活。

• 死亡：其他情况下，一个活细胞将会死亡，要么因为人口稀少（周围活细胞少于三个），要么因为过度拥挤（周围活细胞数多于四个）。

从名字也不难看出，这个游戏希望模拟的是现实的生命过程。即使是刚入门的初学者也很容易写出它的代码（没入门的也可以使用 ChatGPT 代劳），但人们在其中创造出了丰富的生命形式，大致可以分为如下几类：

• 稳定型（Stable Structures）：在没有外界干扰的情况下将保持不变。

• 振荡器型（Oscillators）：将会产生周期性的变化。

• 移动型（Spaceships）：整体将会向一个固定方向移动。

下图展示了一些对应的例子。

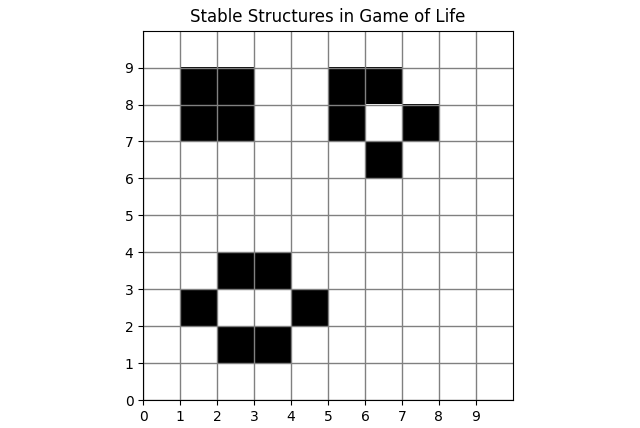
稳定结构

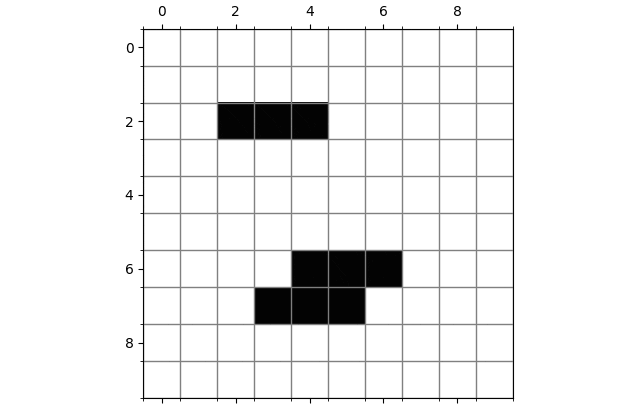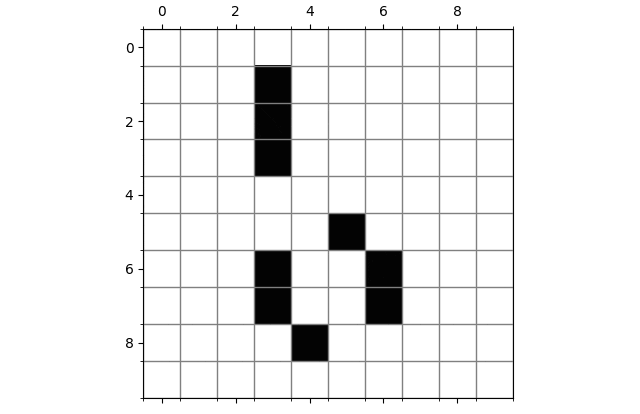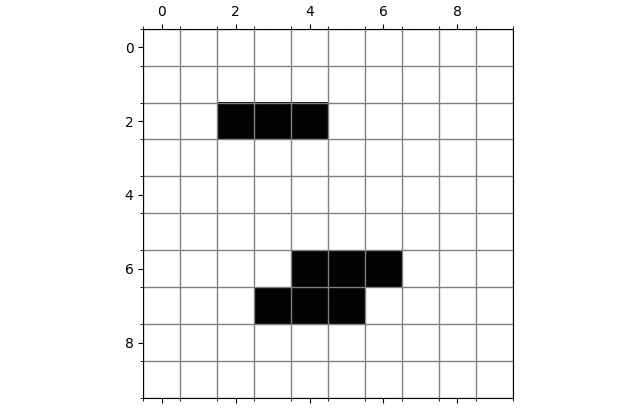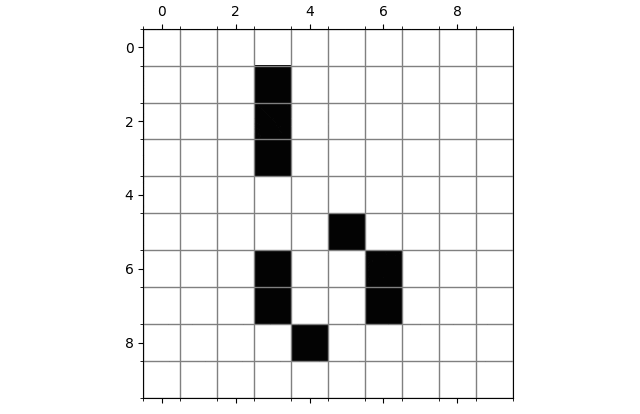
振荡器

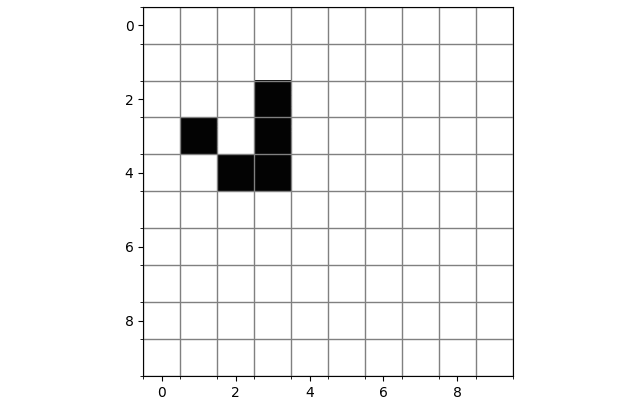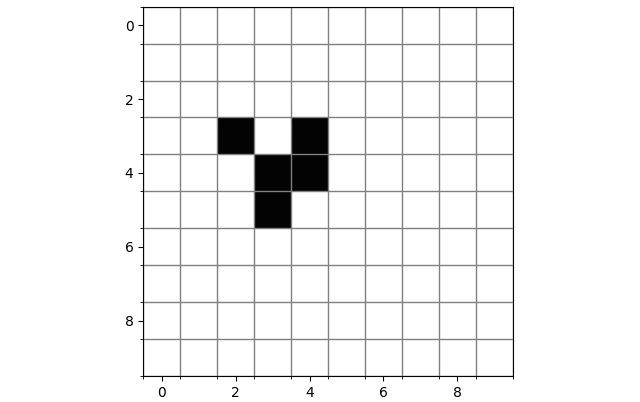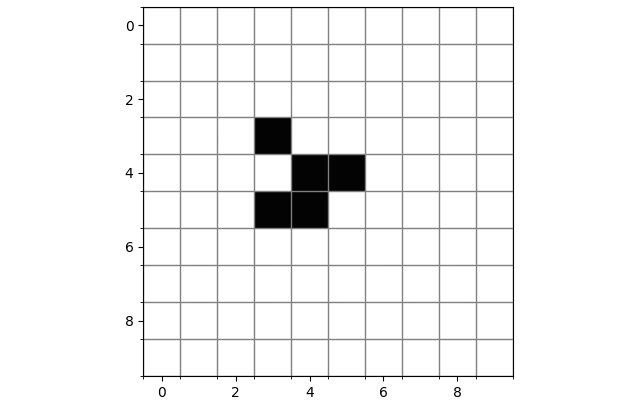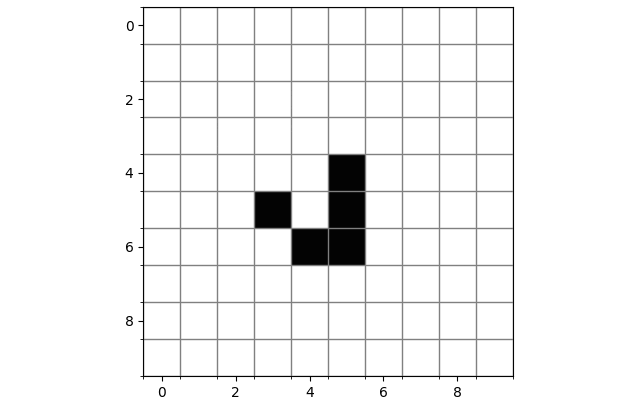
移动物体：这是一个最简单的滑翔机（Glider），仅有五个细胞

上述分类只是冰山一角，生命游戏可以做到的远不止此，例如滑翔机枪（如下图）、时钟[2]。更多的生命则可以参考网站[3]。当然，正如现实一样，大部分的随机生命都没有规律可循，而是在演化中逐渐熵增，走向静止、消亡，或是等待这个空旷的空间里的另一些生命触碰到它们的遗骸，为生命注入新的动力。

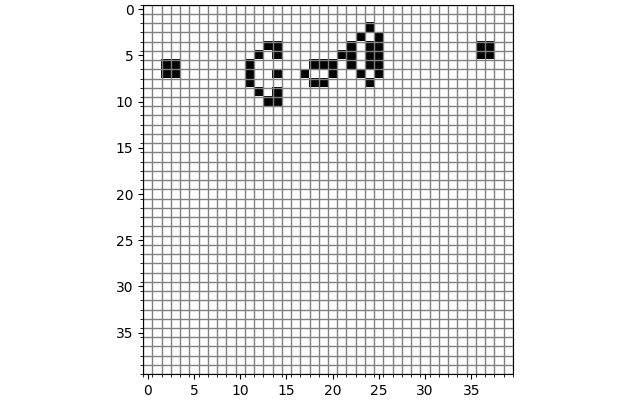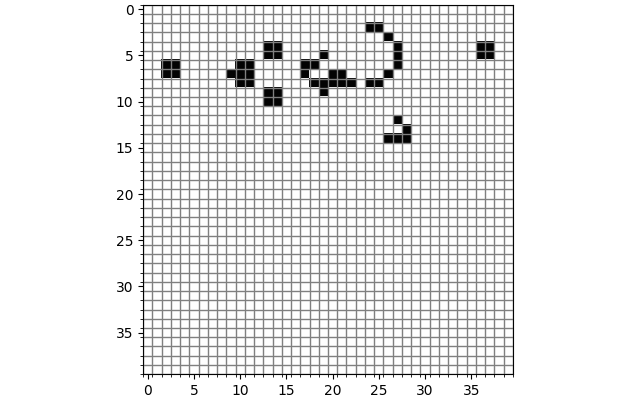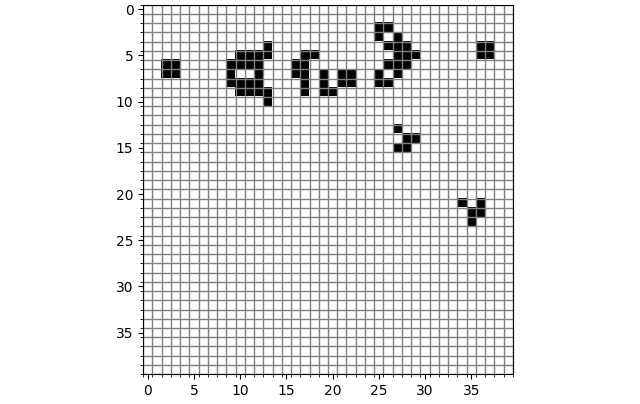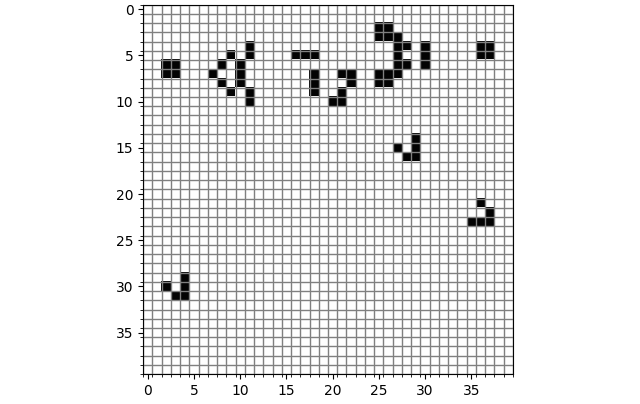
滑翔机枪（Glider Gun）：它会不断发射滑翔机

用生命称呼这些细胞或许不太合适，毕竟它们看上去不过是一些机械般的造物。比起在固定的规则下制造机械，我更喜欢制定规则本身。这也是笔者的科研领域，机制设计（Mechanism Design）的日常，通过规则引导无序的个体展现出特定的行为。

生命创造规则

让我们想象一个一维的 CA，所有元胞排列成环，状态同样只有黑和白。值得一提的是，数学家 Wolfram 对这样的 CA 进行了深入研究，并将他发现的有趣结果写在了书[4]中。对这个名字较为敏感的同学可能已经猜到，他正是著名软件 Mathematica 的作者之一。现在的问题是：我们能否设计一个规则，使得在最后所有的元胞都变为最初占据多数的那个颜色？用术语翻译则是，我们希望设计一个多数者表决（majority vote）的规则。

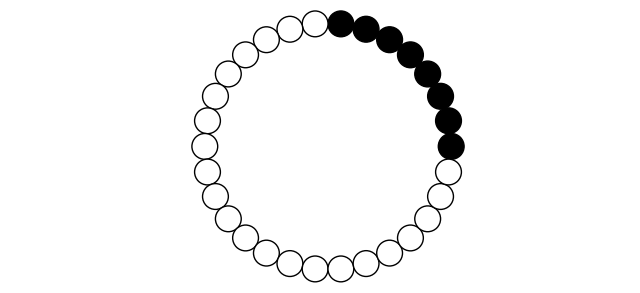
一个最直观的想法或许是，让每个元胞这一回合中邻居中占据多数的颜色成为其下一回合的状态，也就是运行一个局部的多数者表决。可惜的是，这个想法并不奏效，考虑一个黑白分离的环（如下图），这个环在这一规则下是一个稳定的结构，不会发生任何改变，自然也达不到我们的目的。因此这个问题最主要的难点在于，如何判断两个连续同色的元胞串的大小。

要详细列出这个规则本身比较困难，因此笔者仅仅描述其大致想法，具体细节参见文章[5]。还记得我们之前提到的滑翔机吗？我们可以在黑白环的一种边界（例如按照顺时针先黑后白的边界）发射两个不同方向不同颜色相同速度的滑翔机，当一个滑翔机”撞到”另一种边界时，它将通过改变边界颜色的方式破坏这个边界并以更慢的速度反向移动，直到另一个滑翔机追上它结束这个过程。它的原理简单却巧妙，少数者的滑翔机会先碰到另一个边界，多数者的滑翔机则不会碰到边界。

这一规则的发现来自于遗传算法（Genetic Algorithms），一个基于达尔文进化论的算法。这个算法会从一些随机的规则开始，测试它们完成任务的能力，将能力低的规则淘汰，能力高的保留。接下来让存活的规则杂交产生新一代规则，重复这个过程直到出现一个真正能够完成任务的规则。实际上，像蚁群这样的群体生命早已自发地创造出了属于它们的规则。

一个有趣的问题是要做到这个任务，最小的邻域以及对应的规则是什么？这个问题是良定义的，原因在于当我们把整个空间设置为邻域时，一定能够完成这个任务。实现上述的规则需要六个邻居，因此规则包含  种情况。在这个问题的背后则隐藏着一个经典的复杂度定义——Kolmogorov Complexity，它将实现一个功能的最短的程序的长度定义为这个功能的复杂度。关于什么功能、什么过程、什么规则是复杂的定义可谓百花齐放，在此推荐一本教科书[6]。不可否认的是，绝大部分的定义都认为，元胞自动机是一个复杂性的温床。

要说明这一点，回到我们开头提出的问题，如何通过元胞自动机生成锥螺的复杂图案？答案便是 Wolfram 的 Rule30，假如我们用1和0表示黑和白，现在考虑一个只受左右邻居影响的 CA，它的变换规则为，当邻居元胞的状态为111、110、101、100、011、010、001、000时，下一个状态分别为0、0、0、1、1、1、1、0（二进制数11110正是十进制的30，因此得名）。假如我们从只有一个黑色元胞的世界开始，逐步演变，并将时刻  的状态画在一张方格纸的第  行，最后将在这张纸上得到类似开头的图案。

最后，生命和规则就是这样一个递归嵌套的过程，正如大刘的《朝闻道》中所说，溯本追源，探索这样的规则本身正是一些人的终极理想，希望能够与君共勉。

参考文献

[1] Gardner M. The Fantastic Combinations of John Conway’s New Solitaire Game’Life[J]. Sc. Am., 1970, 223: 20-123.

[2] https://codegolf.stackexchange.com/questions/88783/build-a-digital-clock-in-conways-game-of-life/111932#111932.

[3] http://wwwhomes.uni-bielefeld.de/achim/freq_top_life.html.

[4] Wolfram S. A new kind of science[M]. Champaign, IL: Wolfram media, 2002.

[5] Mitchell M, Crutchfield J P, Das R. Evolving cellular automata to perform computations: A review of recent work[C]//Proceedings of the First International Conference on Evolutionary Computation and its Applications (EvCA’96). 1996.

[6] Mitchell M. Complexity: A guided tour[M]. Oxford university press, 2009.

文 | 郭永康

图 | 朱成轩

—   版权声明  —

本微信公众号所有内容，由北京大学前沿计算研究中心微信自身创作、收集的文字、图片和音视频资料，版权属北京大学前沿计算研究中心微信所有；从公开渠道收集、整理及授权转载的文字、图片和音视频资料，版权属原作者。本公众号内容原作者如不愿意在本号刊登内容，请及时通知本号，予以删除。