数学推理与AI：机器学习系统能在多大程度上理解数学？

导语

2023年12月的 NeurIPS 会议上举办了许多主题研讨会，其中 MATH AI 研讨会为第三届，主题为“数学推理与AI”。数学推理是人类认知的基本方面，涉及分析复杂信息、识别模式和关系以及从证据中得出逻辑结论，在科学、工程、金融和日常环境中有着重要应用。最近大语言模型（LLMs）的进展在人工智能和数学推理的交叉领域开辟了新机遇，从解决复杂问题或证明定理的新方法，到数学及其他领域中人机协作的新形式。

NeurIPS 近三年都有针对 MATH AI 的研讨会，其中 2023年共包含 41 篇文章，本文按以下八个主题分类整理（类别间可能存在交叉）：（1）形式化（2）研究导向（3）数据集（4）工具 & 智能体（5）数学推理 & 应用题（6）小模型实验 & 训练微调（7）多模态（8）认知科学。

研究领域：人工智能，大语言模型，数学推理，多模态，控制论，认知科学

王至宏 | 作者

历年 MATH AI 研讨会的链接：

• 2021 年：MathAi4ED 研讨会（Math AI for Education: Bridging the Gap Between Research and Smart Education，https://mathai4ed.github.io/）
• 2022 年：MathAI 研讨会（Toward Human-Level Mathematical Reasoning，https://mathai2022.github.io/）
• 2023 年：MathAI 研讨会（Mathematical Reasoning and AI，https://mathai2023.github.io/）

此外还有

• ICLR’21 MathAI 研讨会（The Role of Mathematical Reasoning in General Artificial Intelligence，https://mathai-iclr.github.io/）

目录

1. 形式化

2. 研究导向

3. 数据集

4. 工具 & 智能体

5. 数学推理 & 应用题

6. 多模态

7. 小模型实验 & 训练微调

8. 认知科学

1. 形式化

形式化相关的文章有 8 篇，除去程序验证的一篇，其余均与定理证明有关，且不少在 LEAN 社区里有单独的帖子在讨论。形式定理证明指在逻辑和数学中，用形式化方法根据一套既定规则去证明定理。这种证明过程不依赖于直观或其他非形式化的推理，而是完全依靠严格定义的符号和操作规则。在形式定理证明系统中，定理是从公理（不证自明的基础陈述）和先前已证定理出发，通过一系列允许的推理步骤得到的结论。这些推理步骤遵循特定的、被该系统认可的推理规则或转换规则。形式定理证明的目的是提供一个完全客观和可验证的证明过程，使得任何了解该形式体系的人都能够检查证明的正确性，而不需要对证明本身进行主观判断。这在数学基础研究、计算机科学中的程序验证等领域有着重要应用。

1.1 LLEMMA：一个开放的数学语言模型

论文地址：https://mathai2023.github.io/papers/45.pdf

代码地址：https://github.com/EleutherAI/math-lm

预训练数据集：https://huggingface.co/datasets/EleutherAI/proof-pile-2

文章提出了 LLEMMA，一个专注于数学领域的大型语言模型。通过在 Proof-Pile-2 上对 Code Llama 继续进行预训练，从而得到 LLEMMA。其中 Proof-Pile-2 是由科学论文、包含数学内容的网络数据和数学代码混合的数据集。此外，Llemma 能够使用工具和进行形式定理证明，而无需任何微调。在 MATH 基准测试中，LLEMMA 超越了所有已知的公开发布的模型，甚至在参数相同的情况下也超过了未公开发布的 Minerva 模型系列。他们公开发布了所有工件，包括 7B 和 34B 参数模型、Proof-Pile-2，以及实验的复现代码。

Llemma 在自然语言问题和形式化语言问题上都表现出了非凡的能力：

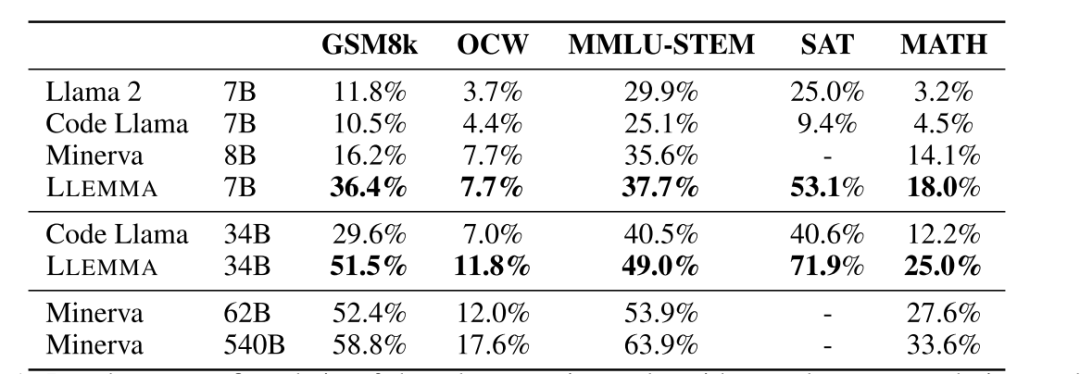
自然语言能力

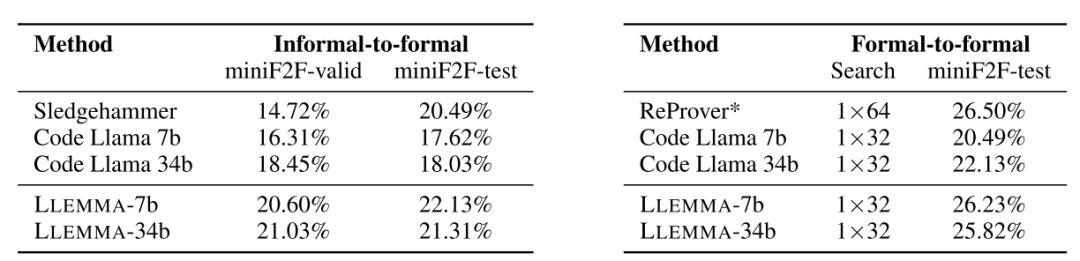
形式化语言能力。左侧：给定形式命题、自然语言命题和自然语言 LaTeX 证明，生成 Isabelle 形式证明；右侧：给定形式命题，生成 Lean 形式证明

这个工作对标谷歌的 Minerva 模型，模型开源且训练数据和代码完全公开，可以作为后续开展其他数学实验的基础模型

1.2 llmstep：基于 LLM 的 Lean 证明步骤建议

论文地址：https://mathai2023.github.io/papers/40.pdf

代码地址：https://github.com/wellecks/llmstep

基础模型：https://github.com/EleutherAI/pythia

这是一个基于 LeanDojo 的非常具有实用性的工作，论文作者 Sean Welleck 八月份就在社区开了帖子 llmstep （https://leanprover.zulipchat.com/#narrow/stream/219941-Machine-Learning-for-Theorem-Proving/topic/llmstep）并开放代码。附带地，其提供了一个实用的插件，如下所示：

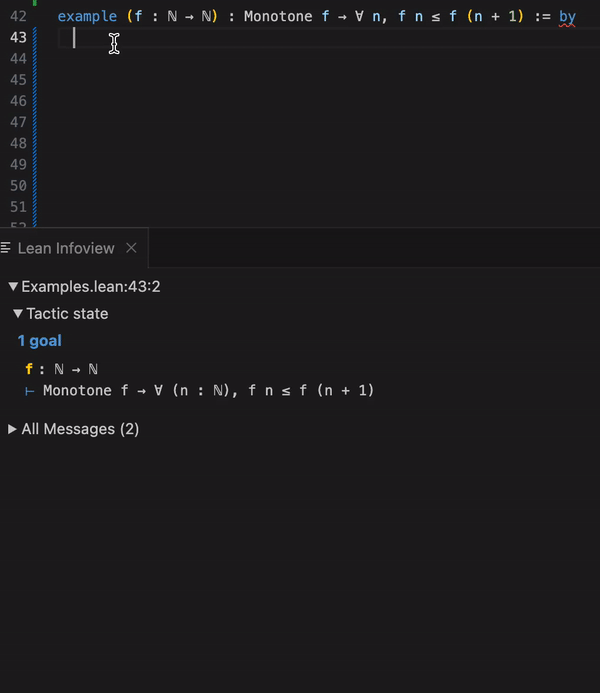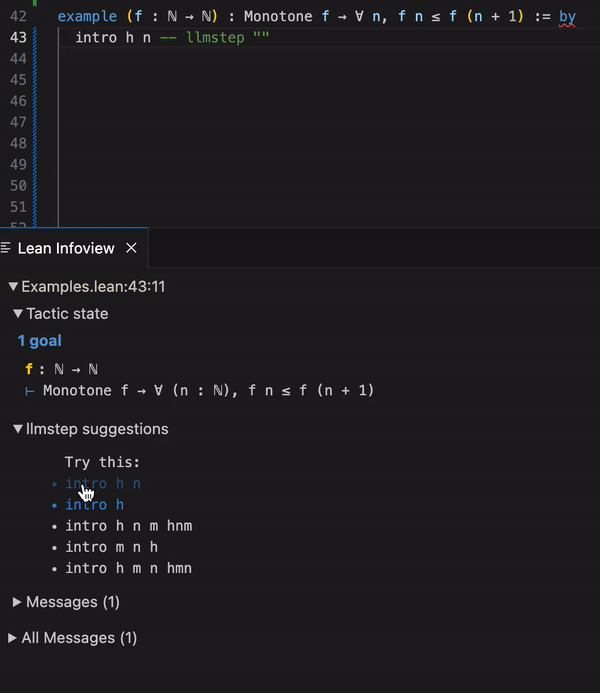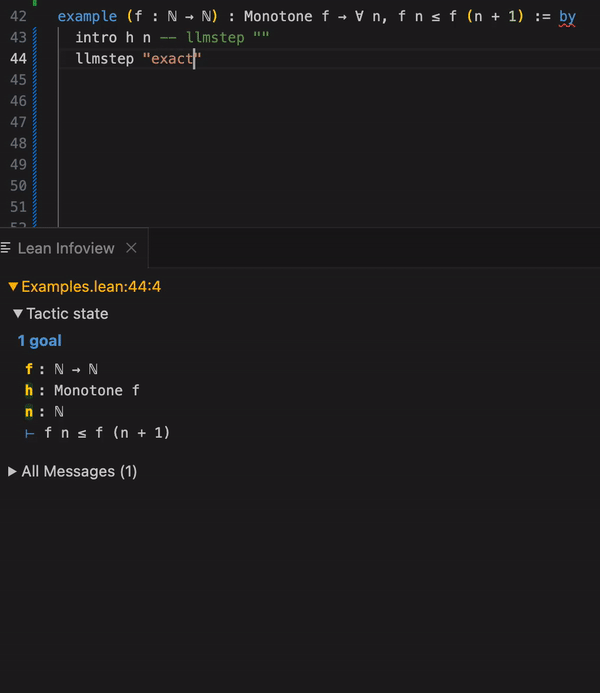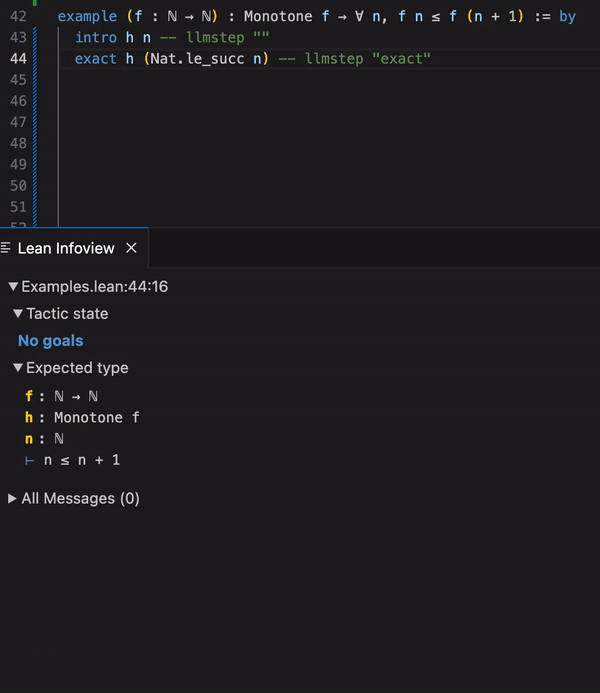
llmstep 示例-vscode

LLMSTEP 是一个集成语言模型至 Lean 证明助手的工具。它通过 Lean4 策略(tactic) 将用户的证明状态发送给托管有语言模型的服务器（下图左侧），然后调用模型会生成建议，这些建议随后在 Lean 中进行检查，并在用户的开发环境内显示（下图右侧）。研究团队提供了一个语言模型基准，并且提供了用于微调和评估的代码，以支撑未来的发展。他们还实现了几种服务器选项，包括在 CPU、CUDA GPU 或 Google Colab 笔记本上运行的服务，旨在为一般用户提供快速且有效的语言模型建议。

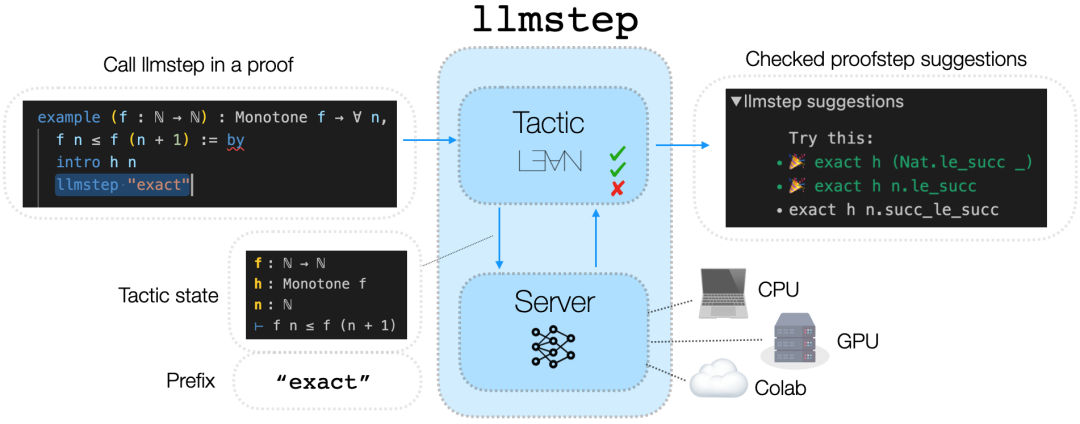
原理图：左侧对接机器，右侧对接人类

默认地，llmstep 基于开源模型 Pythia 2.8b 使用 LeanDojo 数据集进行微调，但具体实现与模型无关，因此支持使用任何语言模型。

1.3 基于语言代理的形式定理证明方法

论文地址：https://mathai2023.github.io/papers/29.pdf

代码地址：https://github.com/trishullab/copra

社区帖子：https://leanprover.zulipchat.com/#narrow/stream/219941-Machine-Learning-for-Theorem-Proving/topic/COPRA

该研究团队提出了一种使用语言代理的方法，COPRA (In-Context Prover Agent)，并在形式定理证明任务中展现出了最新的性能。该方法将大型语言模型（GPT-4）作为执行状态回溯搜索的策略组成部分。在搜索过程中，该策略能够选择适当的证明技巧，并从外部数据库中检索引理和定义。所选的每个策略都在底层证明框架内执行，且执行反馈被用来构建下一次策略调用的提示信息。此外，该搜索过程会追踪其历史信息，利用这些信息减少幻觉现象和减少不必要的LLM查询。研究团队在 Lean 的 miniF2F 基准测试以及 Compcert 项目的 Coq 任务集上对 COPRA 进行了评估。结果显示，在这些基准测试中，COPRA 的性能显著优于单次调用 GPT-4 以及其他在证明数据上进行微调的最先进模型，尤其是在快速找到正确证明的能力方面。

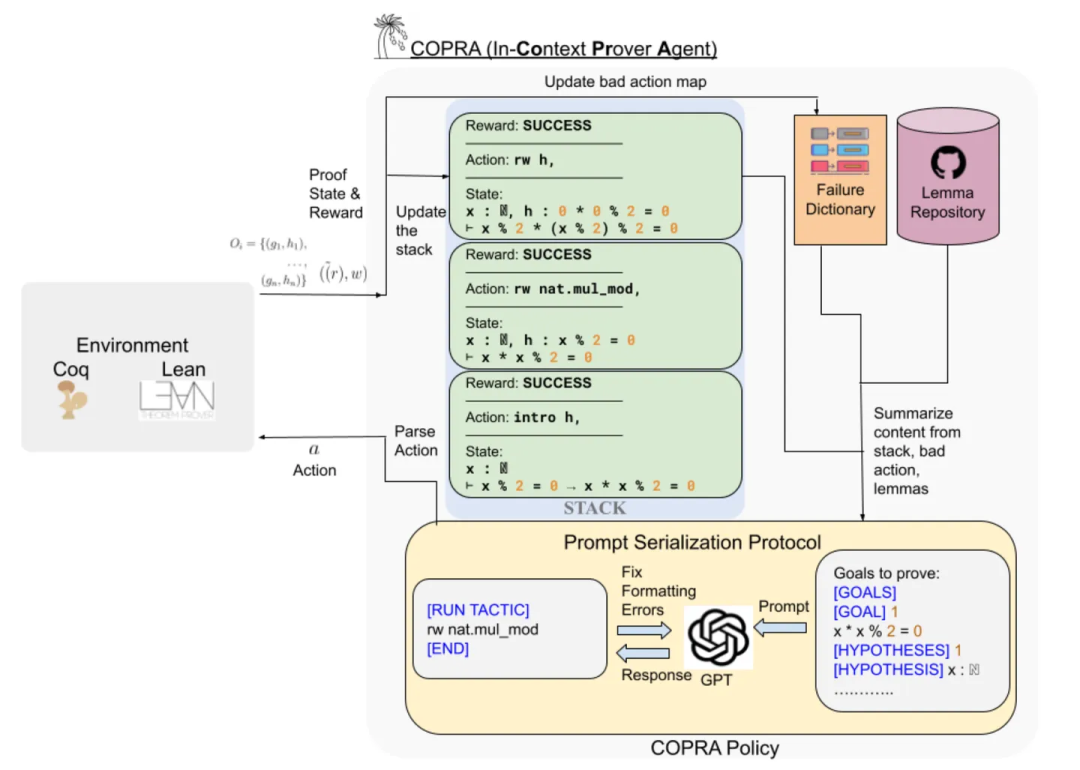
策略生成流程示意图

将执行证明的反馈状态存储下来，用于指导下一次决策。这篇工作同时也是 ICLR2024 的在投文章（https://openreview.net/forum?id=XCMbagV0No）

1.4 Lemur：将大语言模型集成到自动程序验证

论文地址：https://mathai2023.github.io/papers/28.pdf

大型语言模型展示的代码理解能力引发了一个问题：它们是否可以用于自动程序验证，这类任务通常需要对程序属性进行高水平的抽象推理，而这对验证工具来说是极具挑战性的。研究者们提出了一种将 LLMs 和自动推理器的能力结合起来用于自动程序验证的通用方法。他们形式地描述了这种方法，并将其形式化为一系列推导规则，并证明了其正确性。研究者将这个演算体系实例化为一个可靠的自动验证过程，在合成程序以及竞赛数据集上都取得了实际的改进效果。

这个工作主要是面向程序验证

1.5 基于大语言模型温度缩放的 Lean 证明步骤预测

论文地址：https://mathai2023.github.io/papers/25.pdf

利用大型语言模型（LLMs）的推理能力来进行定理证明是个充满希望但又富有挑战性的任务。这项任务需要在特定领域内进行微调，但大型语言模型容易过拟合。这个问题因为两个原因而变得更加严重：一是像 Lean 或 Isabelle 这样的形式化环境中训练数据的稀缺性；二是使用评估基准进行超参数搜索和模型选择的成本过高。在本研究中，他们提出了温度缩放作为小数据集上多轮训练的正则化方法，并通过实验证明了其有效性，在 Lean3 上得到了 1.5B、7B 和 13B 参数的监督式策略的 SOTA 生成模型。此外，作者们对证明搜索的超参数做了详细的消融实验，分析所得模型的证明搜索行为，并展示了基于策略的证明搜索与时间预算约为对数增长规模。

1.6 Magnushammer：基于 Transformer 的前提选择方法

论文地址：https://mathai2023.github.io/papers/23.pdf

社区帖子：https://leanprover.zulipchat.com/#narrow/stream/219941-Machine-Learning-for-Theorem-Proving/topic/New.20paper.3A.20Magnushammer

数据集：https://huggingface.co/datasets/Simontwice/premise_selection_in_isabelle

前提选择是自动定理证明中的关键任务，本文介绍了 Magnushammer，一种新颖的前提选择方法。传统上，这一任务依赖于领域知识和工程努力的符号方法。与之相反，此项工作展示了使用 Transformer 架构进行对比训练可以实现更高质量的相关前提检索，而不需要领域知识或特征工程开销。Magnushammer 在性能上超越了交互式定理证明中最先进且广泛使用的自动化工具：Sledgehammer。在 PISA 和 miniF2F 基准测试中 Magnushammer 分别实现了 59.5%（对比 38.3%）和 34.0%（对比 20.9%）的成功率。通过将 Magnushammer 与基于语言模型的定理证明器结合，进一步将 PISA 基准测试的最佳证明成功率从 57.0% 提高到 71.0%。此外，他们还开发并开源了一个用于前提选择的新颖的大型数据集。

1.7 大语言模型作为 Lean 定理证明的“副驾驶”

论文地址：Towards Large Language Models as Copilots for Theorem Proving in Lean，https://mathai2023.github.io/papers/4.pdf

形式化证明可以通过如 Lean 这样的证明助手严格检查，不给模型留下任何幻觉的可能 。现有基于 LLM 的证明器尝试在没有人工干预的情况下完全自动地证明定理。在这种模式下，他们在处理全新且具有挑战性的定理时会遇到困难，对于这些定理，人类的洞察可能至关重要。这篇工作探索了作为协助人类证明定理 Copilot 的 LLMs，Lean Copilot，一个在 Lean 中运行神经网络推断的框架。它使程序员能够构建各种基于 LLM 的证明自动化工具，这些工具可以无缝集成到 Lean 用户的工作流程中。Lean Copilot 工具利用 LLMs 提出证明步骤和完成中间证明目标，实验结果证明了该方法在协助人类方面相比于 Lean 中现有的基于规则的证明自动化更为有效。

这篇工作和 llmstep 类似，但是代码似乎还没有开放？

1.8 LLM 对比 ITP

论文地址：https://mathai2023.github.io/papers/19.pdf

通讯作者主页：Simon Frieder，https://www.snfrieder.org/

社区关联的帖子：https://leanprover.zulipchat.com/#narrow/stream/219941-Machine-Learning-for-Theorem-Proving/topic/Bangalore.20talk.20on.20LLM.2BITP

形式化的100个定理：https://www.cs.ru.nl/~freek/100/

GHOSTS数据集：https://github.com/friederrr/GHOSTS

GHOSTS关联文章：https://arxiv.org/pdf/2301.13867.pdf

数据集：https://llmknow.friederrr.org/ （链接未开放）

Wiedijk 的 100 个定理列表为比较交互式定理证明器（ITP）及其数学库提供了一个基准。而正如 GHOSTS 数据集所展示的，大型语言模型（LLM）也可以作为可搜索的数学库，因为它们在预训练或微调阶段能够吸收大量的数学文献。ITP 库是唯一可与其媲美的、在规模和数学复杂性范围上相当的资源库。本文以 Wiedijk 的列表为中心，提出了首次将这两种独特的数学资源进行比较的研究。除了对此类比较本身的兴趣外，文章以 GPT-4 和 Claude 2 为代表，讨论了“LLM 中包含的知识是否与 ITPs 中编码的知识相匹配”这一问题的重要性。这种分析进一步推进了 LLM 和 ITP 技术之间的交集（例如自动形式化、由 LLM 引导的证明生成或证明完成等任务），确保 LLM 除了具备 ITP 代码生成能力外，还拥有执行所需形式化的充足数学知识。这一调查结果的数据集称为“LLMKNOW”，已向公众开放。

这篇工作很有意思，相当于在解释为什么 “大语言模型能用于形式定理证明”，以及判断某个模型是否有这方面的能力。

2. 研究导向

这个类别指面向科学研究领域的工作，区别于针对中小学的应用题竞赛题或常规的推理题，这些工作探索 AI 在数学研究方面的应用潜力。第一篇是评估综合能力的基准，后边几篇涉及：代数组合，极值图论，量子计算，动力系统，控制论，材料科学等领域的问题。

2.1 SCIBENCH：评估大型语言模型在大学水平科学问题的解决能力

论文链接：https://mathai2023.github.io/papers/44.pdf代码地址：https://github.com/mandyyyyii/scibench

随着大型语言模型的发展进步，其在许多数学基准测试中取得了显著进展。然而，这些基准测试大多只包含初高中科目的问题、仅设有选择题，并且限制在基本算术运算的狭窄范围内。为了解决这些问题，这篇 论文介绍了一个全面的基准测试套件 SCIBENCH，旨在系统地检验解决复杂科学问题所需的推理能力。 SCIBENCH 包含两个数据集：一个开源集，包括一系列大学级别的科学问题；另一个闭源集，包括本科水平考试中的问题。基于这两个数据集，研究者对五个具有代表性的 LLMs 进行了深入的基准测试研究，并采用了不同的提示策略。此外，通过详细的用户研究，研究者得到：没有任何单一提示策略能显著优于其他策略，一些在特定问题解决技能上显示出进步的策略，可能会造成其他技能的下降。

与其他基准的对比：SCIBENCH 中的所有问题都是开放式的、自由回答的问题。它们需要多个推理步骤，其中的计算涉及复杂的算术运算，如微分和积分。许多现有基准，如 ScienceQA 和 GSM8K，只包含基于年级水平科目的问题，缺乏足够的复杂性；尽管像 MATH 这样的其他基准引入了高中水平的问题，但它们只涉及有限的运算范围（四则运算和求幂），不能充分评估 LLM 的推理能力的深度；其次，最近的工作，包括 MMLU、AGIEval 和 CEval，尽管引入了跨越广泛学科的具有挑战性的问题，但主要集中在多项选择题上，而没有提供详细的解决方案，因而无法理解 LLM 的局限性，也无法辨别它们为什么会犯某些错误；这些基准通常来自在线材料，问题后往往紧跟着答案，模型可能在不真正理解问题的情况下直接预测答案。这些潜在的数据泄露为 LLM 评估提供了一条捷径，进一步损害了其有效性。

这个工作提出了数学物理化学三门学科的数据集，并给出 Baseline

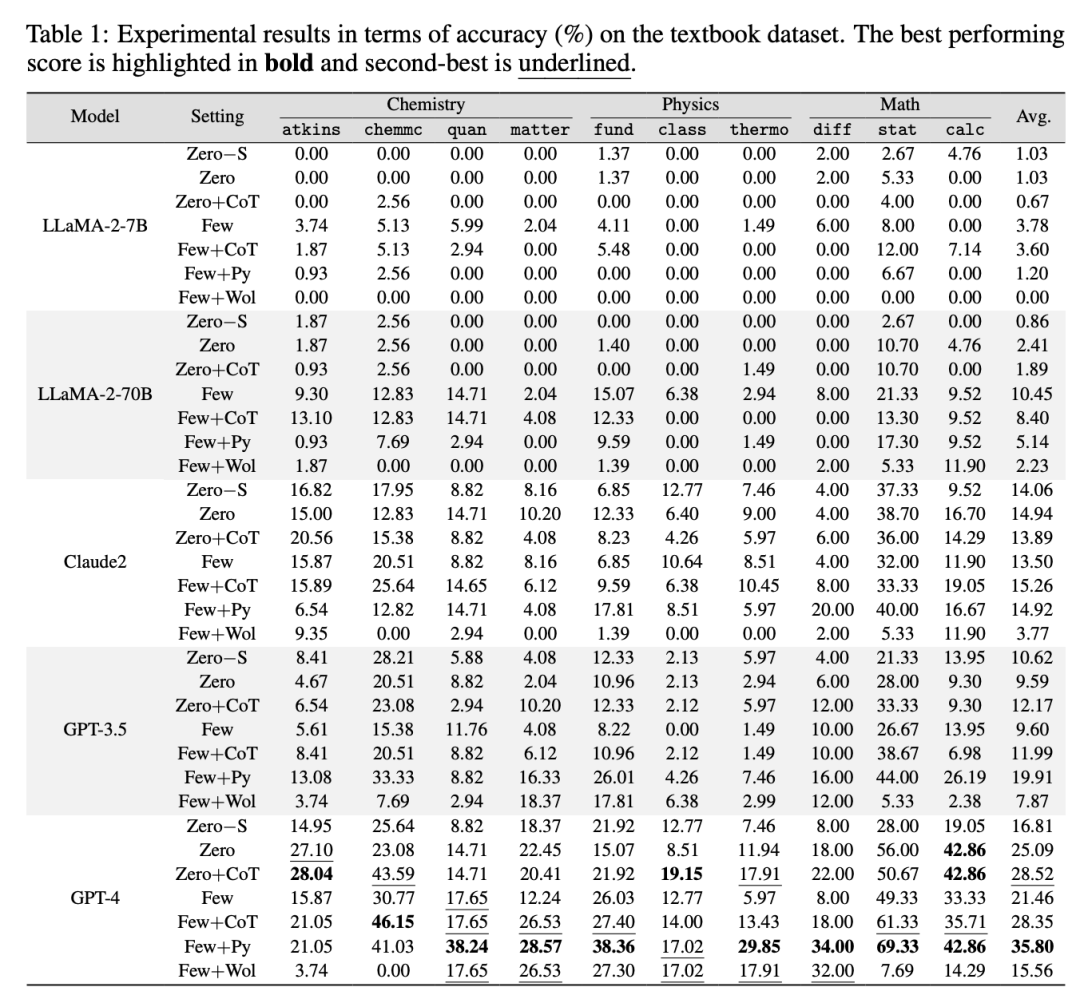
数学物理化学-评测结果

2.2 我们能依赖深度学习吗：使用机器学习探索和表征组合结构

论文链接：https://mathai2023.github.io/papers/10.pdf

深度学习因其出色的模式匹配能力，在多个科学领域中展现了强大的实用性，特别是数学研究领域。近期研究显示深度学习可以发现数学对象间细微关联，这些关联可能被人类专家所忽略。本研究提出一种简单方法，帮助领域专家使用深度学习对数学对象进行表征。当某类函数、空间或线性表示等在计算中自然出现但难以简明描述时，就会面临此类表征问题。总的目标是找到简单的规则，并揭示其中的数学原理。作者开发了一种名为特征归因聚类探索（Feature Attribution Clustering for Exploration, FACE）的方法，通过聚类分析训练模型中的特征归因，得到几种原型归因，专家们可以进一步将这些原型转换为正式且严格的规则。在案例研究中，作者应用该方法在组合数学中取得新成果，表证了一类对应于某些置换表示的0-1矩阵的子集，这些置换表示被称为双边有序词。

这篇工作讨论子集刻画问题（Characterization problem）：给定集合 B 中的一个元素子集 A，找到一种简单的判别方法以确定任意元素 b ∈ B 是否属于 A。

这类问题在数学中无处不在，经典例子包括：

• 一个矩阵是非奇异的当且仅当它的行列式非零。
• 实数空间 Rn 中的一个子集是紧凑的当且仅当它是闭合且有界的。
• 一个图是可展平的(planar)当且仅当它不包含 K5 或 K3,3 作为其子图。

• 本原毕达哥拉斯三元组 (x, y, z) 总是形如 x = r2 − s2、y = 2r·s和 z = r2 + s2的，其中 r 和 s 是正的互质整数。

2.3 使用 AlphaZero 和禁忌搜索寻找非常大的极值图

论文地址：https://mathai2023.github.io/papers/21.pdf

新的极值图：https://storage.googleapis.com/gdm_girth5_graphs/girth5_graphs.zip

前 11 阶简单图的同构类：https://users.cecs.anu.edu.au/~bdm/data/graphs.html

Mathematica 图论工具：https://github.com/szhorvat/IGraphM

本研究探讨了由 Erdos 在 1975 年提出的极值图论的一个中心问题，该问题旨在找到具有给定节点数目的，最大化边数的，不含有3-环或4-环的图 。文章将这一问题形式化为序列决策问题，并比较了 AlphaZero（一种以神经网络指导的树搜索方法）和禁忌搜索（一种启发式局部搜索方法）两种方法。对任一方法，通过引入课程学习——利用在较小规模时找到的好图来加速搜索更大图的过程——文章提高了若干图规模的现行最低边界记录，成为新的 SOTA。文章还提出了一个灵活的图生成环境以及一个排列不变的网络架构，用于学习在图空间中进行搜索。

极值图（Extremal Graphs）是图论中的一个重要概念，其研究目标是在满足某些约束条件下，图的某个参数达到极值的情况。非常经典的例子是Turán图（Turán Graph）。通常，低阶极值图是可以直接暴力搜索。利用 Mathematica 的 IGraphM 暴力求解，用普通笔记本的CPU计算能遍历前 10 阶。但图论问题有个共同特点，随阶数增长计算复杂性通常呈指数增长，下表为每一阶简单图的数据：

1-11阶简单图的数目

常规做法是观察低阶的规律，然后进行归纳证明。但如果希望计算更高阶的例子，就必须采用结合深度学习的策略，比如这篇工作。

下边几篇简单带过，分别涉及量子计算，控制论与动力系统，长度泛化问题，材料科学问题的研究。

2.4 教小型 Transformer 改写 ZX 量子线路图

论文链接：https://mathai2023.github.io/papers/34.pdf相关概念：https://zxcalculus.com/

ZX 演算（ZX calculus) 是一个用于推理线性映射的图形语言。映射通过图表示，而推理则涉及图的改写。ZX 演算主要应用在量子计算领域。研究人员训练了小型 Transformer 模型来简化 ZX 图，即执行量子电路的资源优化。初步实验表明，这些模型可以被训练以高精度简化 CNOT 和 Clifford 电路。这些是最简单类型的 ZX 图，因为它们存在有效的改写策略。此外，还有证据显示，这些 Transformer 模型学会了简化更为复杂的 Clifford + T 图，而这类图通常不存在高效的简化算法。

2.5 强化学习在控制论中的应用：数学问题解决的新方法

论文链接：https://mathai2023.github.io/papers/35.pdf‍

本文介绍了一种结合强化学习（RL）与数学分析的新方法，旨在解决控制理论的一个核心问题：如何通过反馈控制实现稳定性。这项研究特别关注不育昆虫技术（SIT）系统，并致力于找到一个能够稳定蚊子种群模型的反馈控制方式。尽管存在数学复杂性且该特定问题没有已知解决方案，但研究者们的 RL 方法识别出了一个显式稳定控制的候选解。该研究强调了人工智能与数学之间的协同作用，为解决复杂的数学问题开辟了新途径。

2.6 使用 Transformer 探索 Lyapunov 函数

论文链接：https://mathai2023.github.io/papers/13.pdf

本文考虑了数学中一个长期存在的开放问题：探索控制动力系统全局稳定性的 Lyapunov 函数。作者们提出了一种生成训练数据的方法，并训练了序列到序列的 Transformer 模型，以高精度预测多项式和非多项式系统的 Lyapunov 函数。此外，他们还引入了这个问题的新基准，并展示了他们的模型达到了新的 SOTA，超过了基于近似的技术和平方和算法常规程序。

2.7 Transformer 可以学哪些算法？一项长度泛化的研究

论文链接：https://mathai2023.github.io/papers/47.pdf

大语言模型表现出令人惊讶的涌现泛化特性，但在许多简单的推理任务上，例如算术和奇偶性判断，它们却常常遇到困难。在这项工作中，研究者们集中探讨了长度泛化问题，并提出了一个统一框架来理解 Transformers 在给定任务上 何时以及如何实现长度泛化 。首先，他们展示存在某些算法任务，标准的 Decoder Only 模型经过从头开始的训练后自然而然能表现出强大的长度泛化能力。对于这些任务，研究者们利用 RASP 编程语言证明正确的算法解决方案可以被一个简单的 Transformer 所表示。基于此，他们提出并支持了 RASP-泛化猜想：如果存在一个简洁的、对所有输入长度都有效的 RASP-L 程序，那么 Transformers 倾向于学习一个能够进行长度泛化的解决方案。 随后，他们利用这些洞见为传统上难以处理的任务（如奇偶性判断和加法）开发了新的便签（scratchpad）格式，这些格式在长度泛化方面表现出色。总体而言，这些工作为理解长度泛化机制以及 Transformers 的算法能力提供了一个全新的视角。

2.8 垂直领域的人工智能驱动的科学发现

论文链接：https://mathai2023.github.io/papers/15.pdf

将科学发现的过程自动化一直是人工智能的宏伟目标，如果成功，它将会带来巨大的社会影响。尽管目前取得了令人兴奋的进展，但大多数从实验数据中学习科学方程式的努力都集中在水平发现路径上，即直接在完整假设空间中搜索最佳方程。水平路径具有挑战性，因为相关的搜索空间呈指数级增长。这篇工作探索了另一种方式，垂直路径，该路径以增量方式构建科学方程，从基础模型开始，该模型通过控制变量实验对数据进行建模，在此实验中，大部分变量被视为常数。然后通过添加新的独立变量，使用允许这些变量变化的新的控制变量实验，来扩展先前世代中学到的表达式。这种垂直路径是由人类科学发现过程所启发的。实验证明，这样的垂直发现路径加快了符号回归，并且在计算材料科学中描述纳米结构演变的物理模型的学习方面取得了改进。

3. 数据集

部分工作比如：SCIBENCH，在前边已经出现，就不重复讨论了。随着大模型能力的不断提升，很多基准测试正在失去其作为评估工具的作用。与之对应，一些难度更大，面向更加细分领域的数据集被提了出来。

3.1 SIRD：符号积分规则数据集

论文链接：https://mathai2023.github.io/papers/39.pdf

数据集：https://github.com/mfbalin/SIRD-Symbolic-Integration-Rules-Dataset

随着神经网络和计算机硬件的不断进步，深度学习在自然科学领域的新应用场景正日益增多。尽管符号数学任务已得到一定的探索，但关于符号积分的研究却仍然较少，特别是那些使用黑箱模型的研究，并且这些研究通常缺乏可解释性。符号积分本身是一个充满挑战的搜索问题，其最终结果需要在每一步骤中应用不同的积分规则来获取。本文提出了一种新颖且可解释的方法，该方法通过预测积分规则来利用深度学习进行符号积分，以加快搜索过程。作者们提出了第一个此类的符号积分规则数据集，其中包含两百万个独特的函数与积分规则配对。该数据集还包括了应用诸如 u-替换和分部积分法等复杂规则所需的表达式。此外，文章在这一数据集上训练了一个 Transformer 模型，并将其融合进 SymPy 的 integral_steps 函数，从而创造了 guided_integral_steps。这个方法通过允许该模型指导深度优先搜索程序，使得探索的分支数量减少了6倍。

对 Sympy 的改进，但文章似乎没和 Mathematica 进行比较。

3.2 ARB：面向大型语言模型的高级推理基准

论文链接：https://mathai2023.github.io/papers/7.pdf

大型语言模型（LLMs）在各种数量推理和知识基准测试中表现出了惊人的性能。然而，随着 LLMs 越来越高的得分，许多这样的基准测试正在失去其作为评估工具的效用，尽管它们还没有在这些领域达到专家级别的表现。研究者们介绍了ARB，这是一个由高级推理问题构成的新颖的基准，其涵盖了数学、物理、生物、化学和法律等多个领域，比以往的基准测试提出了更高的挑战标准。作为 ARB 的一部分，研究者们提出了一系列需要进行高级符号推理和具备深层领域知识的数学与物理题目。他们对最近的模型如 GPT-4 和 Claude 在 ARB 上的表现进行了评估，结果显示当前模型在更具挑战性的任务上的得分远远低于50%。为了改善自动和辅助评估能力，研究者们引入了一种基于评分标准的评估方法，允许 GPT-4 对其自身的中间推理步骤打分。他们发现，评注员与GPT-4依据评分标准所做的评估得分之间有良好的一致性。

数据集构成：

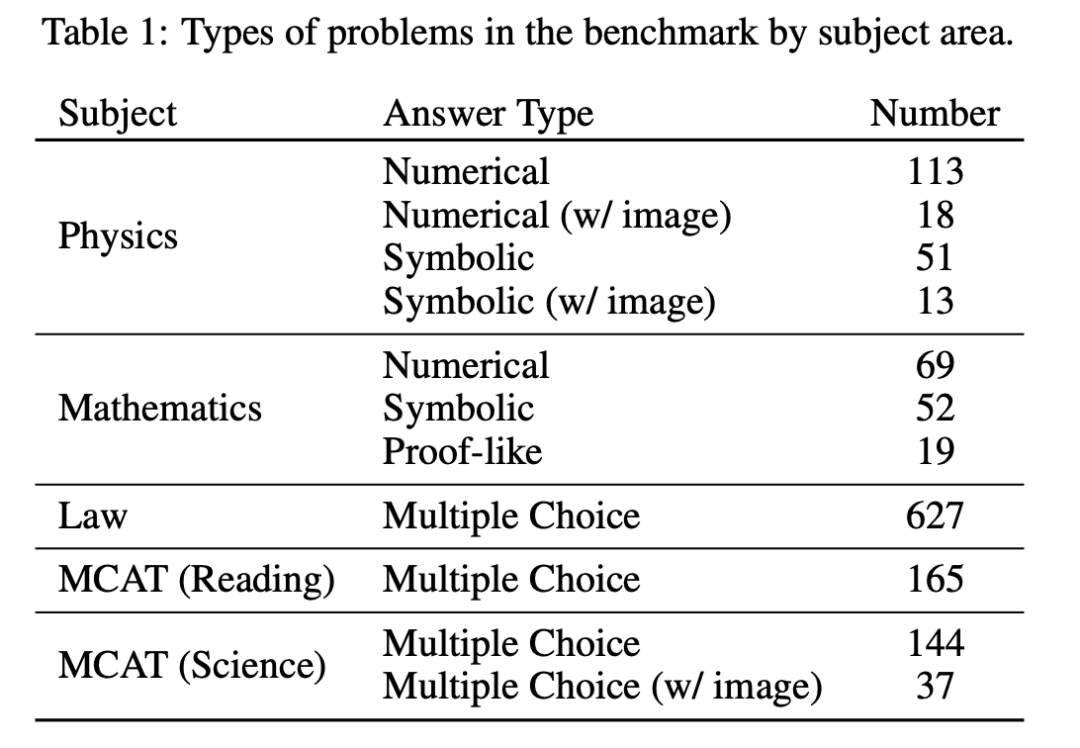
ARB 数据集组成成分

评测效果：

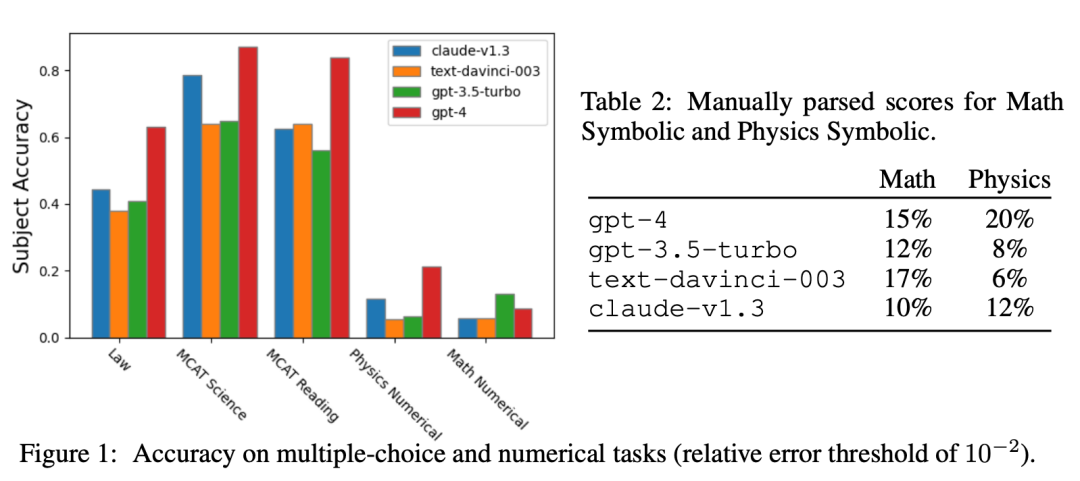
不同模型在 ARB 数据集上的效果

3.3 CHAMP：用于细致分析大语言模型数学推理能力的竞赛级数据集

论文链接：https://mathai2023.github.io/papers/14.pdf代码：https://yujunmao1.github.io/CHAMP

针对挑战性数学问题，目前尚不清楚哪些关于问题的信息是有益的（或者是有害的）。在这篇论文中，作者提出了一个用于此类分析的具有挑战性的基准数据集。命名为“概念和提示注释数学问题”（The Concept and Hint-Annotated Math Problems，CHAMP），该数据集由具有竞赛水平的数学问题组成，并附加了“概念”，即一般数学事实，“提示”，即针对特定问题的策略。这些实体及其相互联系使得研究者能够探索额外信息的影响，如相关提示、误导性概念或相关问题。作者使用4种模型进行了12项初步研究，总结了他们的发现，并讨论了 CHAMP 是如何支持围绕大型语言模型理解与利用上下文的一般讨论。

3.4 OpenWebMath：一个高质量数学网页文本的开放数据集

论文链接：https://mathai2023.github.io/papers/31.pdf

数据集：https://huggingface.co/datasets/open-web-math/open-web-math

越来越多的证据表明，预训练大语言模型在高质量、经过深思熟虑的词元上，如代码或数学内容，对于提升其推理能力起着关键作用。例如，Minerva 这一经过在 arXiv 和网络上数十亿数学文档微调的 PaLM 模型，在需要数量推理的问题上取得了显著进步。然而，目前已知的公开发布的网络数据集在预处理时都没有忠实地保留数学符号，因此无法利用大规模训练网页文档的优势服务于研究社区。研究人员提出来 OpenWebMath，一个受到这些工作启发的开放数据集，包含来自 Common Crawl 的 14.7B token 的数学网页。文章详细描述了从 HTML 文档中提取文本和 LaTeX 内容以及移除样板文件的方法，并且介绍了用于质量筛选和去重的方法。此外，他们在 1.4B 参数的语言模型上使用 OpenWebMath 进行了小规模实验，实验结果显示，基于这些数据集中的 14.7B 词元训练出的模型，在性能上超过了那些在超过 20 倍语言数据量上进行训练的模型。作者们希望这一公开发布的数据集能有助于推动大型语言模型推理能力的进一步发展。

数据过滤过程：

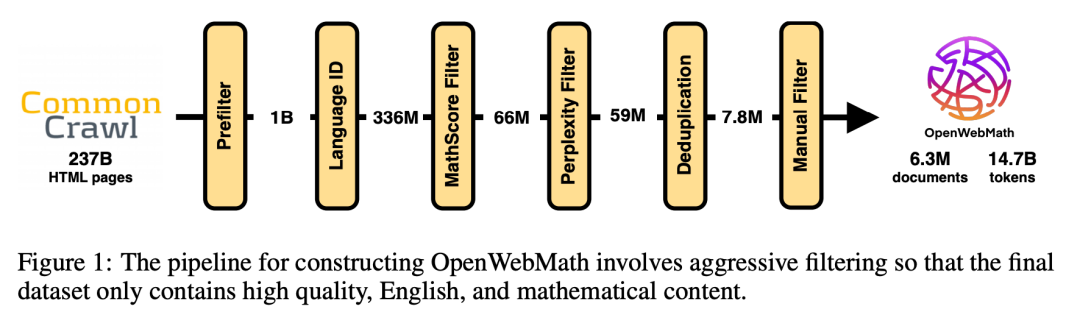
数据清洗 Pipeline

4. 工具 & 智能体

工具是智能体构建中最为重要的一环，其使得智能体能够完成许多单靠 LLM 难以完成的任务。下边几篇工作对数学智能体构建是非常好的参考。

4.1 Chameleon：大型语言模型即插即用的组合式推理

论文链接：https://mathai2023.github.io/papers/51.pdf

代码地址：https://github.com/lupantech/chameleon-llm.git

大型语言模型（LLMs）因其涌现的推理能力，在解决各种自然语言处理任务方面取得了显著进展。然而，LLMs 存在固有的局限性，它们无法访问最新信息（存储在网络或特定任务知识库中）、使用外部工具以及进行精确的数学和逻辑推理。为了减轻这些限制，作者提出了一个名为 Chameleon（变色龙）的人工智能系统。该系统通过增加即插即用的模块增强 LLMs 的组合推理能力。Chameleon 通过组合各种工具（例如，LLMs、现成的视觉模型、网络搜索引擎、Python 函数和基于启发式的模块）来合成程序，完成复杂的推理任务。Chameleon 的核心是一个基于 LLM 的规划器，负责组装一系列工具以执行生成最终响应。在两个多模态知识密集型推理任务 ScienceQA 和 TabMWP 上，Chameleon 证明了其有效性。由 GPT-4 驱动的 Chameleon 在 ScienceQA 上达到了 86.54% 的总体准确率，比最佳发布的 few-shot 结果提高了 11.37%。在 TabMWP 上，GPT-4 驱动的 Chameleon 将准确率提高了 17.0%，将最新技术水平提升到 98.78%。分析还表明，在推断指令中潜在约束时，与 ChatGPT 驱动的规划器相比，GPT-4 驱动的规划器展示了更为一致和理性的工具选择。

两个简单示例，取自在 TabMWP 数据集：

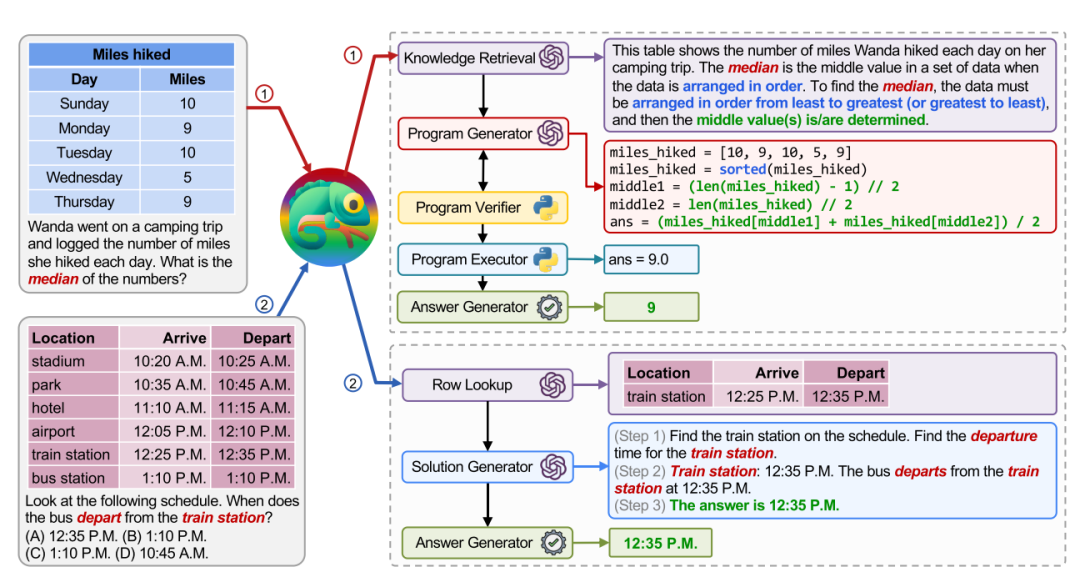
计算路程中位数（上）获取发车时间（下）

这个工作构建了一个智能体，通过组合各种工具来获取答案，且支持一般的 QA 问答，而不局限于数学问题。

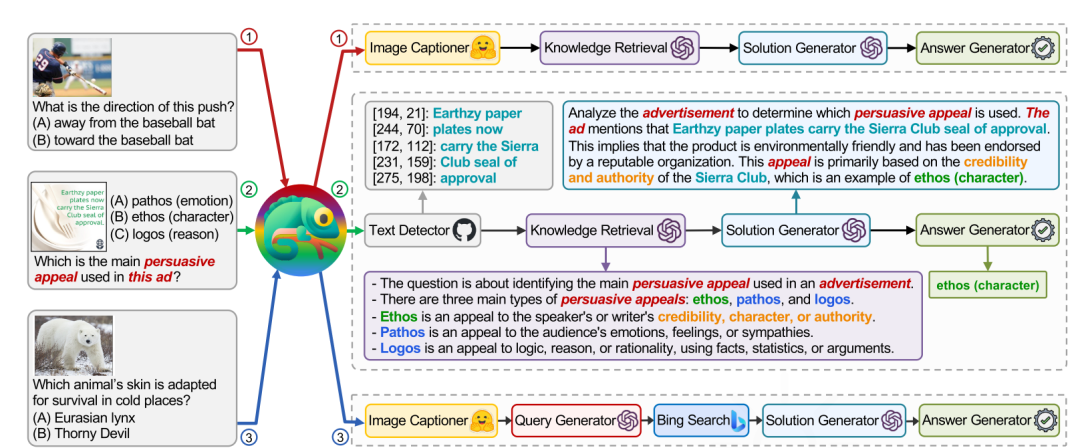
QA + 简单推理

4.2 ToolDec：通过有限状态解码实现 LLM 的无语法错误和泛化性工具使用

论文链接：https://mathai2023.github.io/papers/49.pdf代码地址：https://github.com/chenhongqiao/tooldec

大型语言模型已经展示了在使用外部工具方面的令人瞩目的能力。然而，现有方法依赖于微调或上下文学习来使用工具，这些方法会产生语法错误且难以泛化。本文提出了 ToolDec，一种基于有限状态机引导的解码算法，用于工具增强型 LLM。ToolDec 通过确保工具名称的有效性和参数类型的一致性，消除了与工具相关的错误。此外，ToolDec 使得 LLM 能够仅仅根据工具的名称来有效地选择工具，无需进行针对特定工具的微调。作者们在多个应用题问题数据集上的实验表明，ToolDec 将语法错误降至零，从而显著提升了性能，并且速度提高了最多2倍。研究还显示，在从未见过的工具上，TookDec 的泛化性能比基线高达8倍。

通过有限状态机（FSM）进行引导（结合符号与统计）

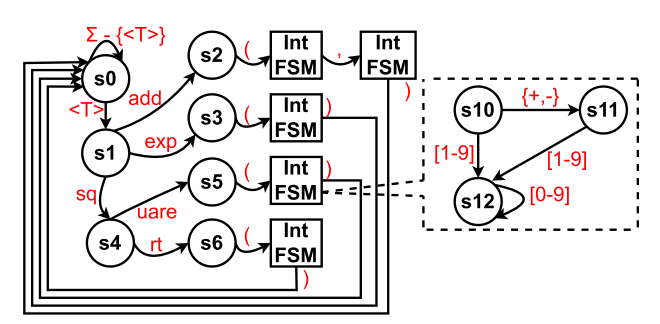
用有限状态机（FSM）进行引导大模型

4.3 结合语言模型与符号求解器解决数学应用题

论文链接：https://mathai2023.github.io/papers/16.pdf代码链接：https://github.com/joyheyueya/declarative-math-word-problem

在教育领域，自动产生高质量的数学应用题逐步解答具有广泛应用。近来，将大型语言模型与外部工具结合起来执行复杂推理和计算，已成为解决数学应用题的一个有前景的研究方向，但是之前的方法如程序辅助语言模型（Program-Aided，PAL）倾向于解决简单的程序性问题，在需要声明式推理的问题上效果不佳。研究者提出了一种新的方法，该方法结合了一个能够逐步将应用题形式化为一组变量和方程的大型语言模型，以及一个能够解这些方程的外部符号求解器。在 GSM8K 数学应用题基准测试中，这一新方法所达到的准确率与原始的 PAL 相当。而在 ALGEBRA 数据集上，它相比 PAL 达到了 20% 的绝对提升。这里 ALGEBRA 是一个从代数教科书中提取的更具挑战性问题的新数据集。这项研究强调了在与外部工具交互解决复杂数学应用题时，使用声明式和增量式表示的优势。数据和提示信息均已开源。

声明式方法的简单示例：

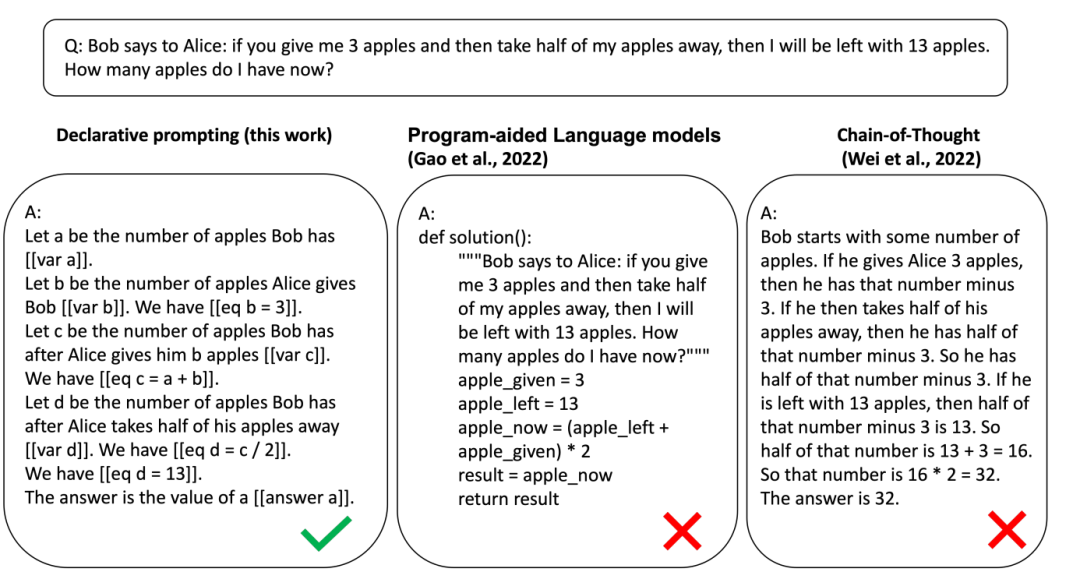
声明式方法（左图）

5. 数学推理 & 应用题

作为区分，这一专题针对应用题或简单任务的数学推理，这次论坛主题就是推理，Workshop on Mathematical Reasoning and AI，大部分论文可以归到此类。

5.1 TinyGSM：通过 1B 参数在 GSM8K 上实现80%准确率

论文链接：https://arxiv.org/pdf/2312.09241.pdf

小型模型提供了诸多计算上的优势，但模型参数量对于解决问题能力的影响程度仍然是个悬而未决的问题。这项工作研究了小型模型在数学推理任务上的表现。具体来说，研究人员发现，一个具有 1.3B 参数的模型在解决数学应用题上能够达到 80.1% 的准确率，这个表现超越了大得多的现有模型，并且甚至可以与其生成训练数据的 GPT-3.5-turbo 教师模型的性能相媲美。论文的方法很简单，主要包含两个关键部分：第一部分是使用一个由 GPT-3.5-turbo 生成的、包含解答的数学应用题合成数据集，该数据集将完全公开。第二部分是使用一个验证器，从多个候选答案中选择最终输出。

5.2 MinT：通过多视图微调提高数学推理的泛化能力

论文链接：https://mathai2023.github.io/papers/55.pdf

数学领域的推理对于相对较小的语言模型（LMs）依然是一个重大挑战。许多现行方法专注于使 LMs 专长于数学推理，并且严重依赖从强大但效率不高的大型语言模型（LLMs）中提取知识。在这项工作中，研究人员探索了一种新方向，避免过度依赖 LLM 教师，引入了一种多视图微调方法，该方法有效利用了具有多样化注释风格的现有数学问题数据集。该方法独特地考虑到各种注释格式作为可能互相帮助的不同“视图”，并在训练模型时利用它们。通过在输入问题后附加不同的指令，模型可以灵活地学会以多种格式生成解决方案。实验结果表明，该策略使相对较小的 LMs 的表现超越了先前严重依赖知识蒸馏的方法，以及精心建立的基线。此外，所提出的方法赋予模型在不同视图和数据集上的潜在泛化能力，以及从不准确或不完整的噪声数据中学习的能力。作者们希望通过多视图训练范式能激发其他机器推理领域未来的研究。

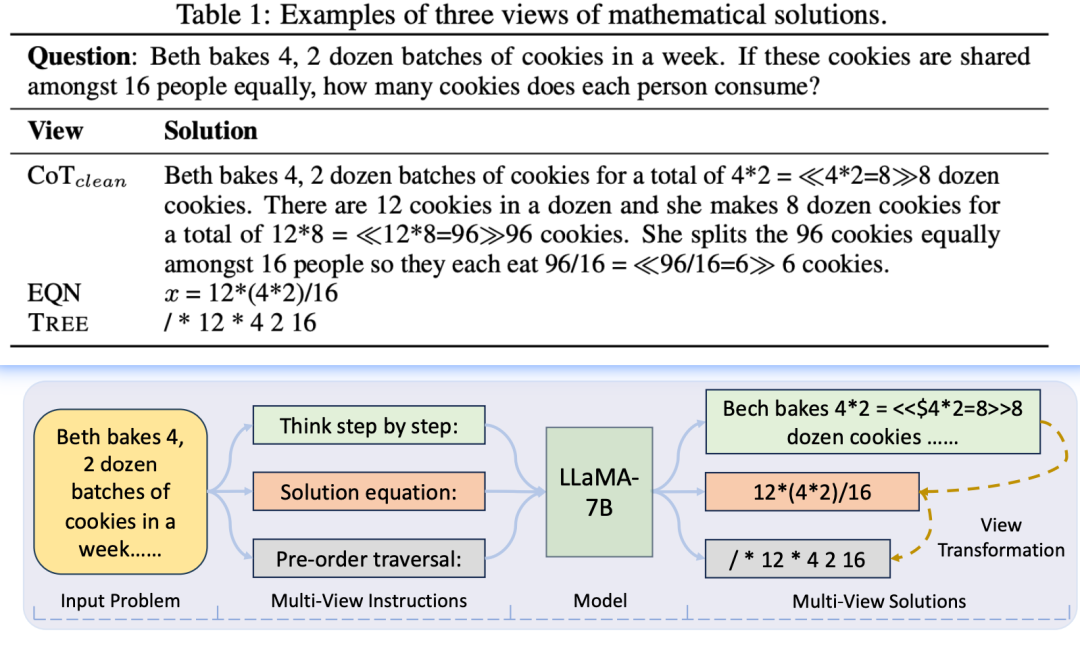
多视图微调数据

5.3 基于符号规则学习的大语言模型，用以增强数值推理鲁棒性

论文链接：https://mathai2023.github.io/papers/46.pdf

ILASP 简介：Inductive Logic Programming Answer Set Programming,

https://www.doc.ic.ac.uk/~ml1909/ILASP_ALP_2020.pdf

虽然人们已经提出了一些提示策略来引导大型语言模型进行推理，但对于机器阅读理解任务，数值推理依然是一个挑战。研究者们提出了一种神经符号方法，利用 LLM 的上下文学习能力将复杂问题分解成更简单的子问题，并采用符号学习方法学习重组部分答案的规则。该方法在 DROP 基准的不同数字子集上进行了评估；结果表明，这种方法与为 DROP 专门设计的 SOTA 模型竞争力相当，并且显著优于纯粹依靠 LLM 提示的方法。此外，该方法具有数据效率高的特点，因为它无需进行任何额外的训练或微调。神经符号方法还促进了鲁棒的数值推理能力，确保模型忠实于其所呈现的文本，并提供可解释和可验证的推理过程。

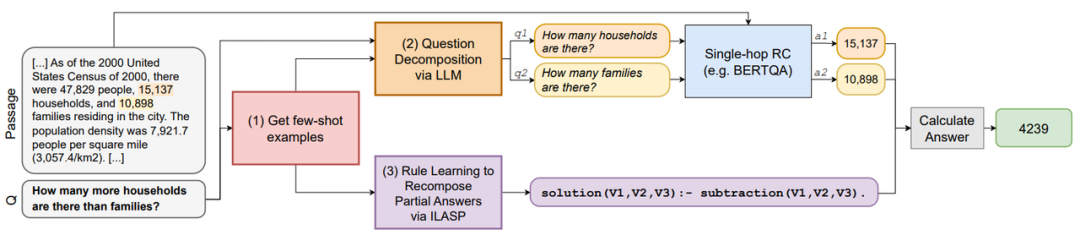
神经符号算法

5.4 计划、验证和转换：多样化思维方式的集成推理

论文链接：https://arxiv.org/pdf/2310.14628.pdf代码地址：https://github.com/tengxiaoliu/XoT

随着大型语言模型展现出在不同提示方法下的有效性，例如“思维链”和“思维程序”（Program of Thought），这些方法在数学推理任务上已经显示出了相互之间的极佳互补性。在这项工作中，研究人员提出了 XoT，一个通过用多样化推理思路启发 LLM 的集成问题解决框架。对于每个问题，XoT 总是先选择最合适的方法，然后迭代执行每种方法。在每次迭代过程中，XoT 会主动检查生成答案的有效性，并纳入外部执行器的反馈，从而能够在不同的提示方法之间动态切换。通过在 10 个主流的数学推理数据集上进行广泛实验，研究者证明了他们所提出的方法的有效性，并彻底分析了每个模块的强项。此外，实验结果表明，该框架与近期在单一推理方法上取得改进的工作相正交，并且能够进一步泛化到逻辑推理领域。通过允许方法间的切换，XoT 为在统一框架内协同集成多样化推理思维提供了新的视角。

5.5 EchoPrompt：通过重述问题提高上下文学习能力

论文链接： https://mathai2023.github.io/papers/22.pdf

代码地址：https://github.com/rajasekharmekala/echoprompt

该文章提出了 EchoPrompt，一种通过让模型在回答问题之前重新表述查询来提升性能的简单而有效的技术。该技术适用于零次提示和少数示例提示的场景，并且能够与标准提示以及思路链提示结合使用。实验结果表明，EchoPrompt 在多个因果语言模型族的各种设置中大幅提升了性能，包括数值推理（例如，GSM8K, SVAMP）、阅读理解（例如，DROP）和逻辑推理（例如，翻硬币）等任务。特别是，它使得 code-davinci-002 模型在零次提示的思路链环境下，在数值任务上的性能提升了 5%，在阅读理解任务上提升了 13%。这些结果显示，EchoPrompt 可以有效地加强在上下文学习过程中的表现，建议将其融入到各类基线提示策略中，以提高整体效能。

这类工作的想法都很简单，让模型在回答前重新表述问题，加强对问题的理解，例子如下：

回答前重新表述问题（右图）

5.6 通过算术任务学习多步推理

论文链接：https://mathai2023.github.io/papers/1.pdf

代码链接：https://github.com/TianduoWang/MsAT

数学推理被视为语言模型所必需的能力。最近的研究表明，大型语言模型在解决数学问题方面有着令人印象深刻的表现。这种成功被归因于它们的“链式思考”（COT）推理能力，即分解复杂问题成为逐步推理链的能力，但这样的能力似乎只出现在参数非常多的模型中。这项工作探讨了如何将多步推理能力整合进相对小型的语言模型中。作者提出通过在一个由多步算术任务（MSAT）组成的合成数据集上继续预训练语言模型来引入这种能力。在数学应用题任务上的实验展示了这一方法在提升语言模型数学推理能力方面的有效性。

5.7 通过重新检验解决数学应用题

论文链接：https://mathai2023.github.io/papers/18.pdf代码链接：https://github.com/steven640pixel/PsedualMWP

解决数学应用题（MWP）的目标是理解描述性数学问题并计算结果，之前的努力大多致力于提升不同技术模块。本文带来了一个不同且新颖的视角——在训练过程中进行重新检验，并引入了一个伪双任务以增强 MWP 解决能力。研究者们提出了一种模型无关的伪双重（PseDual）学习方案，可以适配任何现有的 MWP 解决器。这个特定定义的伪双任务是将数学表达式中的数字重新填充回原始的应用题中，并使数字处于屏蔽状态。为了有效地联合两个任务的学习，研究者还设计了一个预定融合策略，用于数字填充任务，该策略平滑地将输入从真实数学表达式转换为预测的表达式。通过实证研究，伪双重学习方案已被验证在多个代表性MWP解决器中有效。

5.8 SATLM: 使用声明式提示的可满足性辅助语言模型

论文链接：https://mathai2023.github.io/papers/32.pdf代码地址：https://github.com/xiye17/sat-lm

先前的工作将思维链技术与程序化表达结合在大型语言模型（LLMs）中，用以进行推理。这种方法对于只需单向推理的任务（例如，简单的算术问题）效果良好，但对于需要更复杂规划和搜索的问题，则效果不佳。在本文中，作者提出了一种名为可满足性辅助语言建模（SATLM）的新方法来增强 LLMs 的推理能力：利用 LLM 生成一个声明式任务说明而非命令式程序，并且借助现成的自动定理证明器来得出最终答案。通过将实际推理任务外包给自动定理证明器，这种方法能够保证相对于解析出的规格的答案的正确性，并避免在解题过程中发生规划错误。该研究在 6 个数据集上评估了 SATLM 的表现，并指出它在命令式范例中持续超越了程序辅助 LLMs 的性能。特别地，在 GSM 算术推理数据集的一个具有挑战性的子集上，SATLM 比程序辅助 LLMs 的性能高出 20% 以上；同时，在法学院入学考试（LSAT）和 BOARDGAMEQA 上，SATLM 也达到了新的 SoTA。

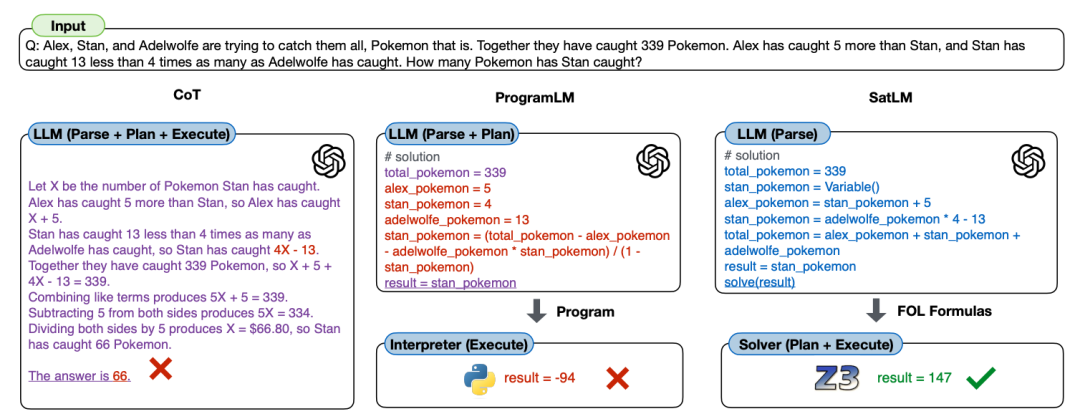
三种模式对比图

5.9 语言模型提示空间中基础算术性质的研究

论文链接：https://mathai2023.github.io/papers/24.pdf

最近，能够有效利用大量未标注文本数据的大型预训练神经语言模型（LLMs）彻底改变了自然语言处理领域。通过利用这些模型固有的上下文学习能力支持的提示技术，已经证明 LLMs 能够与为下游任务专门训练的模型相媲美。其中一个任务是数值推理，特别是进行基本算术运算的能力。研究者们探讨了算术运算的基本性质，例如交换律，在LLM提示的环境下是否依旧适用——即要求LLM计算13 + 37与37 + 13是否通常会导致相同的结果。与之前大多数只报告准确度的工作不同，他们通过更仔细地观察错误分布（平均绝对误差、皮尔逊相关系数R），来更好地理解在提示扰动和规模法则下的性能表现。

6. 多模态

6.1 MathVista：在视觉上下文中评估基础模型的数学推理能力

论文链接：https://mathai2023.github.io/papers/52.pdf论文网站：https://mathvista.github.io/

尽管大型语言模型（LLMs）和大型多模态模型（LMMs）在不同领域展现了令人印象深刻的技能，但它们在视觉背景下进行数学推理的能力尚未正式评估。为LLMs和LMMs装备这种能力对于通用目的AI助手至关重要，并且在教育、数据分析和科学发现等方面展现出巨大潜力。

为填补这一空白，研究者提出了 MATHVISTA 基准测试，该测试旨在结合来自文献中识别出的多样化的数学和视觉任务挑战。研究者首先从28个现有的以数学为焦点和视觉问答数据集中，归类并确定了关键的任务类型、推理技能和视觉背景。然后构建了三个新的数据集，即IQTest、FunctionQA和PaperQA，以覆盖缺失的视觉背景类型。所呈现的问题通常需要超越光学字符识别（OCR）或图像字幕的深入视觉理解，并且要求使用丰富的领域特定工具进行组合推理，这对现有模型来说是一个显著的挑战。研究者对11个知名的开源和专有基础模型（包括LLMs、增强工具LLMs和LMMs）进行了全面评估。表现最佳的模型——多模态巴德（Multimodal Bard），仅达到了人类性能的58%（34.8%相比60.3%），表明改进的空间仍然很大。鉴于这一显著的差距，MATHVISTA激励了未来的研究，推动通用AI代理的发展，使其能够处理数学密集型和视觉丰富的现实世界任务。

6.2 用于家庭数学学习的口语理解评估

论文链接：https://mathai2023.github.io/papers/41.pdf

随着最近在会话式人工智能技术方面的进步，借助互动式数学学习家庭系统提升早期儿童教育质量正逐步变成现实。本研究通过实施一种多模态对话系统，在家中支持基于游戏的学习体验，引导儿童掌握基础数学概念。研究团队探索了任务导向型对话系统内部的口语理解（SLU）流程，该流程采用了级联自动语音识别（ASR）和自然语言理解（NLU）组件，并在孩子们参与的“儿童空间”家庭部署数据上进行了评估。这些数据来自于孩子们参与的游戏化数学学习活动。研究验证了NLU多任务架构的优势，并且试验了多种预训练语言表示，用于数学学习领域的意图识别和实体抽取。为了在真实家庭环境中识别儿童的语音，研究调查了若干ASR系统，包括谷歌云服务和最新的开源Whisper解决方案，涉及不同大小的模型。通过在带噪声的ASR输出上测试表现最佳的NLU模型，研究评估了SLU流程，以审视在真实家庭环境中理解儿童数学学习语音的挑战。

6.3 通过在向量符号架构中学习规则进行视觉抽象推理的概率归纳

论文链接：https://mathai2023.github.io/papers/20.pdf代码链接：https://github.com/IBM/learn-vector-symbolic-architectures-rule-formulations

抽象推理是人类智能的基石，用人工智能（AI）复制这一能力是一个持续的挑战。该研究专注于通过利用分布式计算和向量符号架构（VSA）提供的运算符，高效地解决雷文递进矩阵（RPM），一种用于评估抽象推理能力的视觉测试。该方法无需硬编码RPM相关的规则公式，而是能够在对训练数据仅进行一次遍历的情况下学习VSA规则公式（因此得名Learn-VRF）。尽管参数紧凑，该方法保持了透明度和可解释性。Learn-VRF在I-RAVEN的分布内数据上提供了准确的预测，并在处理未见过的属性-规则组合时表现出强大的分布外能力，显著超越了包括大型语言模型在内的纯连接主义基线。

7. 小模型实验 & 训练微调

7.1 向小型 Transformer 教授算术

论文链接：https://mathai2023.github.io/papers/36.pdf

代码链接：https://anonymous.4open.science/r/nanoGPT-25D2

即使是小型 Transformer，在接受大量文本数据训练后，也能够展现出在基本算术等通用任务上的涌现能力，尽管这些任务并没有通过无监督的下一个词预测目标明确编码。本研究调查了从随机初始化开始训练的小型 Transformer，如何高效学习算术运算（比如加法、乘法和求平方根等初级函数），使用下一个词预测目标。研究证实，传统训练数据并不是最有效地进行算术学习，并且简单的格式更改可以显著提高模型的准确性。这导致了训练数据规模函数的剧烈相变，在某些情况下这可以通过与低秩矩阵补全的联系来解释。基于已有的工作，研究者在包含中间步骤结果的链式思维风格数据上进行训练。即使在完全没有预训练的情况下，这种方法也显著地同时提高了准确性、样本复杂性和收敛速度。研究也考察了训练过程中算术与文本数据之间的互动，并检验了少量提示、预训练和参数缩放的效应。此外，文章还讨论了与长度泛化相关的挑战。该工作强调了高质量、具有指导性的数据的重要性，这些数据考虑到了下一词预测损失的特定特征，以便迅速激发出算术能力。

7.2 学习最大公约数——Transformer 中的可解释预测

论文链接：https://mathai2023.github.io/papers/8.pdf

作者训练了小型Transformer模型来计算两个正整数的最大公约数（GCD），并证明这些模型的预测是完全可解释的。在训练过程中，模型学会了识别一个除数列表D，并且能够预测出该列表中能同时整除两个输入整数的最大元素。研究还表明，训练分布对模型性能有显著影响。仅从均匀分布的操作数进行训练的模型只掌握了少量的GCD（38/100）。当使用对数均匀分布的操作数进行训练时，模型性能提高到正确预测73个GCD，而基于对数均匀分布的GCD进行训练可以进一步提升性能，达到91个正确的GCD。

7.3 系统推理任务中的持续学习与分布外泛化

论文链接：https://mathai2023.github.io/papers/54.pdf

人类经常能够从一系列狭窄的例子中学习新的解决问题策略，并将这些策略泛化到学习过程中未曾涉及的实例，但神经网络在此方面的泛化能力仍然面临挑战。这种限制影响了数学技巧的学习，这些技巧适用于无界的问题空间（例如，所有实数）。研究者利用神经网络探索了这一局限性，它们在训练解决6×6数独谜题的特定单元格的策略时使用了一种新颖的课程——模型首先学习两个初级任务，随后研究者在训练更复杂解决策略可能会遇到的训练样例子集期间评估其分布外泛化能力。基线模型能够掌握训练分布，但未能在分布外进行泛化。然而，研究者介绍了一组足以支持高准确度和可靠的分布外泛化的扩展组合。这些结果为增强在自然数据集中由于数据分布高度不平衡而训练出的模型的健壮性提供了新的方向。

7.4 多样化监督的原则探索

论文链接：https://mathai2023.github.io/papers/17.pdf

通过下一个词预测来训练大型 Transformer 模型，推动了AI领域的重大进步。尽管这种生成式 AI 的方法取得了显著成果，但它极度依赖于人类监督。即便是像ChatGPT这样的最先进AI模型，也需要通过人类演示进行微调，这要求大量的人工输入和领域专业知识。这种对人类监督的高度依赖成为AI创新发展的一个重要障碍。为了应对这一挑战，研究者们提出了一个被称为探索性AI（EAI）的新范式，其目标是自主生成高质量的训练数据。EAI从无监督强化学习（RL）的预训练中汲取灵感，在自然语言空间实现探索。该方法利用大型语言模型来评估生成内容的新颖性，并包含两个关键组成部分：一个按照探索原则生成新颖内容的“行动者”和一个评估并提供指导性批评以引导行动者的“评价者”。实证评估显示，EAI在复杂推理任务上显著提升了模型性能，克服了对人力密集型监督的依赖限制。

8. 认知科学

8.1 AI for Mathematics: 认知科学视角

论文链接：https://mathai2023.github.io/papers/38.pdf

数学是人类种族开发和使用的最强大的概念系统之一。自动化数学家的梦想在人工智能（AI）的历史中占有一席之地。特别是大型语言模型（LLMs）的飞速进步重新点燃了广泛兴趣，促使人们建立此类系统。本文从认知科学的视角反思这些目标。作者指出了几个认知科学领域中既经典又持续的研究方向，认为这些方向对于那些寻求构建真正达到或超越人类水平的数学系统的AI实践者极为重要。文章最后提出了一些开放性问题，认为解决这些问题需要多学科合作：认知科学家、AI研究员以及数学家共同努力，以期构建更好的数学AI系统，这不仅可以推进数学的边界，还能揭示人类如何具备完成这样伟大认知任务的能力。

8.2 卷积神经网络模型对数量概念的敏感性

论文链接：https://mathai2023.github.io/papers/37.pdf

数的本质是数学哲学中的一个经典议题。认知科学家已证实，人类心理上将数字表示为组织成心理数线（MNL）的量级。本研究探讨了在学习分类图像时，卷积神经网络模型是否会无意中学到关于数字和数量的概念。事实确实如此。一个代表性的模型显示出距离效应、大小效应和比例效应，这些都是人类数量表示中的标志性特征。通过对其潜在表示进行多维尺度分析（MDS），研究者发现这些表示与人类所记录的心理数线有着密切的相似性。这些发现挑战了发展科学中的观点，该观点认为数字是所有人类婴儿固有的“核心知识”，并且提供了数字概念可学习性的存在证明。

作者简介

王至宏，华东师范大学计算机学院在读博士，本硕基础数学专业。本科获全国大学生数学竞赛决赛一等奖，全国高校数学密码挑战赛中南赛区二等奖等竞赛奖项，硕士自学 GAP，SageMath 等代数编程语言，探索 Programming For Math，当前方向为大语言模型与基础数学的融合研究。学者主页：https://pattern.swarma.org/master/878

在集智俱乐部「人工智能与数学」读书会中，王至宏做了主题为“智能体与数学的交汇”的分享，介绍智能体在数学领域的应用，读书会回放视频已经上线，感兴趣的朋友可以深入了解。https://pattern.swarma.org/study_group_issue/570

人工智能与数学读书会

数十年来，人工智能的理论发展和技术实践一直与科学探索相伴而生，尤其在以大模型为代表的人工智能技术应用集中爆发的当下，人工智能正在加速物理、化学、生物等基础科学的革新，而这些学科也在反过来启发人工智能技术创新。在此过程中，数学作为兼具理论属性与工具属性的重要基础学科，与人工智能关系甚密，相辅相成。一方面，人工智能在解决数学领域的诸多工程问题、理论问题乃至圣杯难题上屡创记录。另一方面，数学持续为人工智能构筑理论基石并拓展其未来空间。这两个关键领域的交叉融合，正在揭开下个时代的科学之幕。

为了探索数学与人工智能深度融合的可能性，集智俱乐部联合同济大学特聘研究员陈小杨、清华大学交叉信息学院助理教授袁洋、南洋理工大学副教授夏克林三位老师，共同发起“人工智能与数学”读书会，希望从 AI　for　Math，Math　for　AI 两个方面深入探讨人工智能与数学的密切联系。

详情请见：

人工智能与数学读书会启动：AI for Math，Math for AI

推荐阅读

1.  数学探索的未来：从AI引导人类直觉到数学大语言模型2. 人工智能与数学前沿综述：如何借助 AI 发现数学规律？3. 当机器学习遇见拓扑：拓扑数据分析与拓扑深度学习4. 张江：第三代人工智能技术基础——从可微分编程到因果推理 | 集智学园全新课程5. 加入集智学园VIP，一次性获取集智平台所有内容资源6. 加入集智，一起复杂！

点击“阅读原文”，报名读书会

​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​