从分解到整合：整合信息分解框架｜周日直播·因果涌现读书会第四季

导语

复杂系统可以看做存在相互作用的多变量系统，而信息论是理解变量之间关系的重要视角。然而，传统的信息论指标往往难以捕捉多个变量协同产生的作用，为此人们提出部分信息分解框架（PID），将多变量之间的互信息分解为各种信息原子，来度量其对某一目标变量的交缠相互作用，并在此基础上进一步提出整合信息分解框架（ΦID），将目标变量从一个延拓到多个，真正可以应用在多变量复杂系统上。这样从分解到整合的计算可以看做是“互信息的微积分”。本文是对提出ΦID的理论文章的解读。

在集智俱乐部「因果涌现」读书会第四季本周日（1月21日）的分享中，北京师范大学系统科学学院硕士生杨明哲将在之前信息分解的基础上，继续介绍整合信息分解框架（ΦID）。该框架可以帮助我们重新拆解已有的各种复杂性指标，通过信息原子的组合，清晰地看到为什么一些经典的整合信息指标有时会出现负值。更重要的是，我们可以基于整合信息分解框架设计出度量系统复杂性的指标，应用在因果涌现的定义和识别上。

论文题目：Beyond integrated information: A taxonomy of information dynamics phenomena.

论文地址：http://arxiv.org/abs/1909.02297

问题源起：从分解到整合

信息论是我们研究复杂系统常用的工具。它可以绕过具体的复杂非线性作用关系，直接度量变量之间的相关程度和信息传递过程。比如我们会关心政府投入对国家GDP增长的影响，其中有着长期且复杂的作用链，通过信息论的指标可以直接计算观测数据中各指标之间的相关程度，非常简洁地反映出指标间的因果关系。
随着我们关心的系统变量不断增多，作用关系更加复杂，传统的信息论不够用了。比如经济系统中一项关于企业的政策可能关乎多个指标，其作用在市场上，最终也会同时影响生产和消费。变量和变量间都可能存在着或强或弱的关联，使得诸如多个变量协同在一起产生的作用无法被主流的信息论指标所捕捉。为了解决这样的问题，Williams和Beer提出部分信息分解框架（PID）[2]，可以度量多个变量对某一目标变量的交缠相互作用大小，包括冗余信息、协同信息和特有信息。
继PID提出之后，我们对复杂系统各种现象的研究就有了新工具，比如我们能否把这样的框架应用在复杂系统的因果分析中？传统对时间序列的因果分析都是从单因到单果，比如格兰杰因果检验，分析的是某一变量的时间序列对另一个变量是否存在因果关系，本质上是在计算信息论里的转移熵。但是，当研究对象有更多的变量，我们便需要工具能够分析多因到多果的过程，即下式所表示：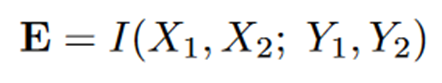

其中Xi表示第i个变量在t时刻的取值，Yi则表示它在t+1时刻的取值。这样的互信息算出来，表达的就是一个过程的过剩熵（excess entropy）。基于PID已有的经验，我们知道这里面一定存在协同信息、冗余信息、特有信息等等高阶关系，而且会比之前见过的三变量系统还要复杂很多。Rosas等人便拓展原有的PID框架，提出整合信息分解（ΦID）[1]，能够把整个过剩熵分解成若干个信息原子，从而重新诠释已有的整合信息度量指标，并提出新的修正指标，可以用来捕捉一个复杂系统的各方面性质。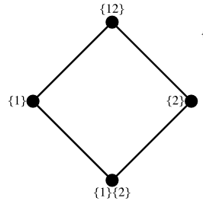

PID框架的冗余晶格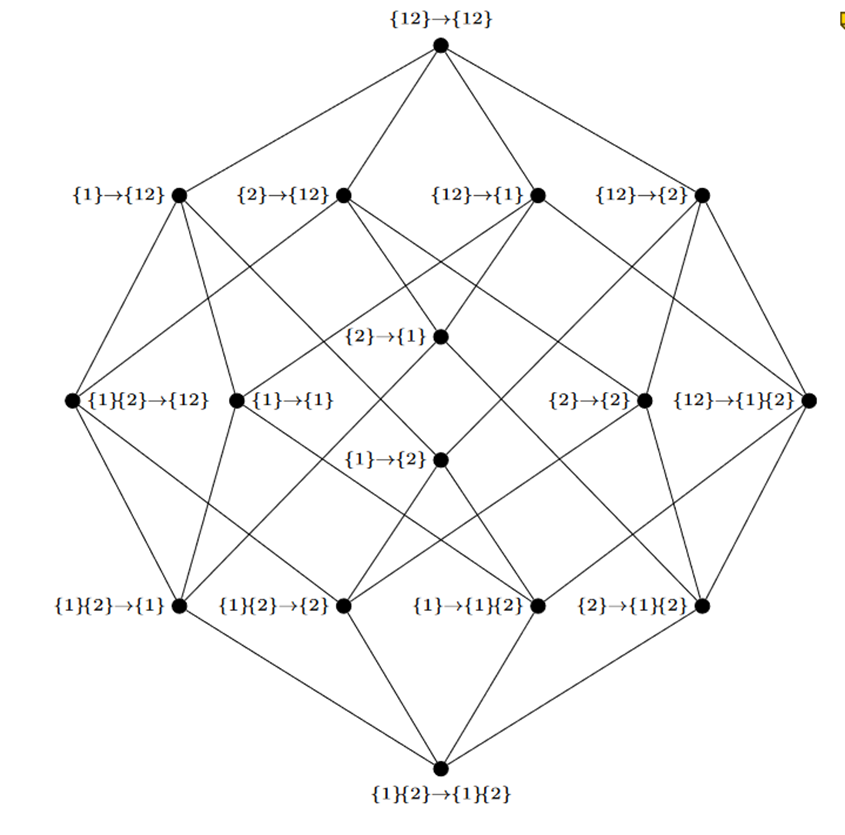
ΦID框架的冗余晶格，共有16个信息原子
是的，为了度量一个复杂系统的整合程度大小，学者们已经提出过各种整合信息指标[4]。但他们皆有缺陷，无法在所有场景下都能够适用。

比如一个经典的整合信息指标是 whole-minus-sum，其计算方式如下式所示：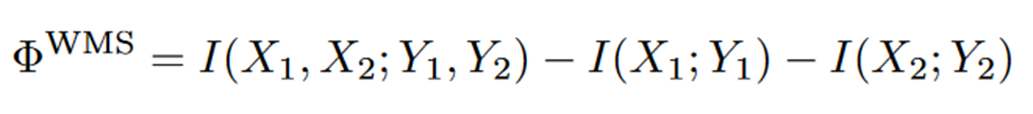

可以看出，它度量的是把一个系统按变量划分后出现的信息损失。可是在有些情况下，它会算出负值。这意味着什么呢？为了深刻理解这些指标背后的机理，我们需要深入了解一下整合信息分解的框架。

整合信息分解框架：从PID到ΦID

为了能理解ΦID，我们需要重新来看PID的冗余晶格。因为它研究的是两个变量到一个特定的目标变量的联合互信息，所以在画冗余晶格时，可以省略目标变量，而实际上每个格点对应的分别都是三变量系统下的冗余、协同或特有，均为信息原子，是联合互信息的一部分。而当目标变量从一个变成两个，冗余晶格就要从原先的4个，扩增到4*4=16个。考虑两个变量的动力学演化过程。如果用PID的框架描述，当把t时刻两个变量看做一个变量，则是向后PID；当把t+1时刻两个变量看做一个，则是向前PID。而ΦID可以同时包括这两个过程，甚至还可以度量向前和向后PID都捕捉不到的信息原子，比如X1到Y2的信息传递。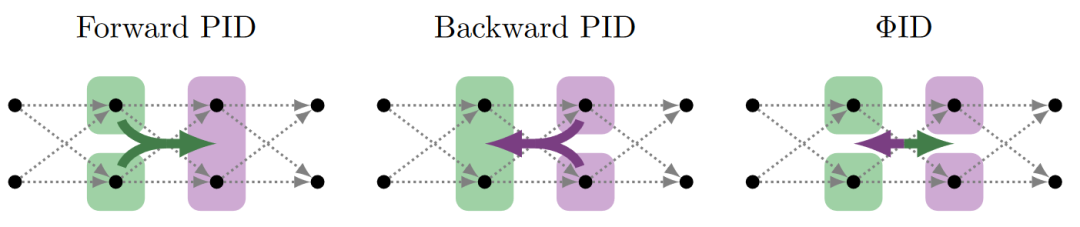

文章里没有告诉我们如何更合理地计算信息原子，可以沿用Beer的计算方式（详见《互信息的“微积分”》）或者其他已有的计算方法（虽然各有些缺陷）[5]。不过文章提供了两个公理，是任何计算方法需要符合的。一个是说当源变量或目标变量中的某一个只有一个变量时，ΦID会退化为PID框架。另一个则是说更高阶的冗余信息一定会大于等于低阶的冗余信息。
信息原子要怎么区分高阶与否呢？实际上这里的偏序关系继承了Beer的定义。如下式所示，当某一个信息原子的两端都处于PID冗余晶格的低阶位置时，就可以判定该信息原子是更低阶的。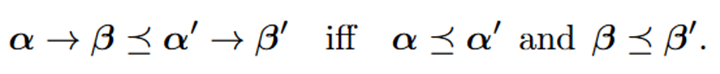

同样如法炮制，在计算信息原子时，只要给出初始最低阶冗余信息的计算方法后，整个冗余晶格上所有的信息原子都可以递归地计算得出。如下式所示：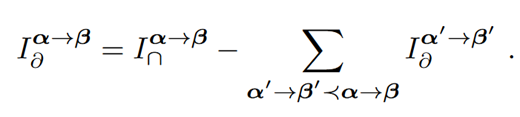

对这样递归算法不熟悉的读者可回顾往期对PID框架计算的讲解。
因果涌现读书会第四季分享吕奥博：多源变量信息测度https://pattern.swarma.org/study_group_issue/598

整合信息指标的拆解

有了上面的ΦID框架，我们就可以将其应用在某些例子上，来看看信息传递中有哪些精细的结构在以往被我们忽略了。我们考虑两个离散变量的动力学过程，如下图所示，有三个不一样的动力学过程。左图过程是把X1复制直接得到Y2，其他变量状态独立随机取值。中图是对X1，X2做异或运算，得出的结果与Y1相等。右图则是X和Y分别做异或运算，得出的结果要保持相等。注意这里的X和Y分别对应t和t+1两个时刻。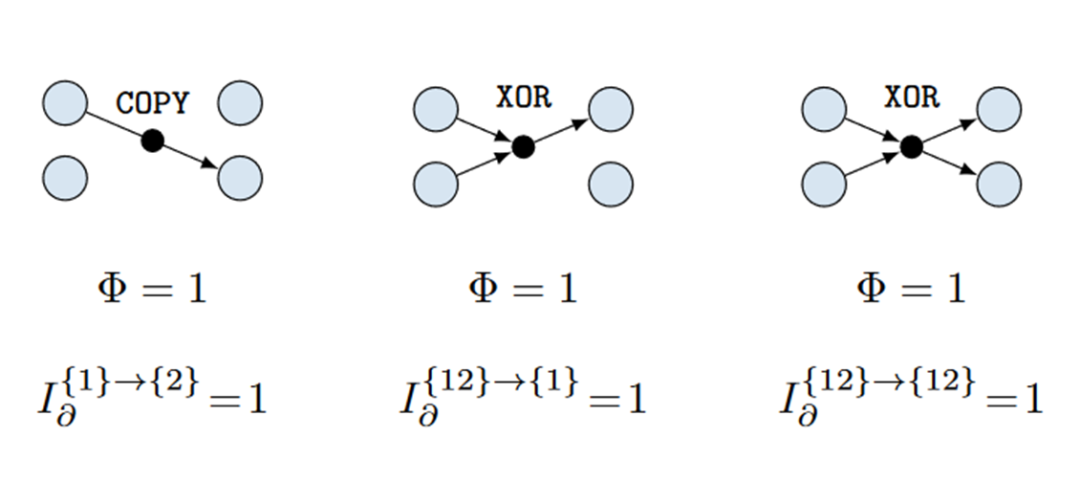图片来源[1]
这三个过程有明显的不同。第一个过程类似于信息在两个变量之间的转移（transfer），第二个过程则是两个变量放在一起决定一个变量在下一时刻的取值，是向下因果（downward causation），第三个过程则像是信息在一个更宏观的层次上一直留存着（storage）。如此不同的三个过程，如果用whole-minus-sum来计算，得出的结果都是一样的，无法区分，而用ΦID的框架就可以通过信息原子的组合清晰地反映出来。
事实上作者给所有信息原子分了类，除了上面三种以外，还有向上因果（upward causation），擦除（erasure），复制（copy），一共六种。它们在冗余晶格上的分布如下图所示 [7]。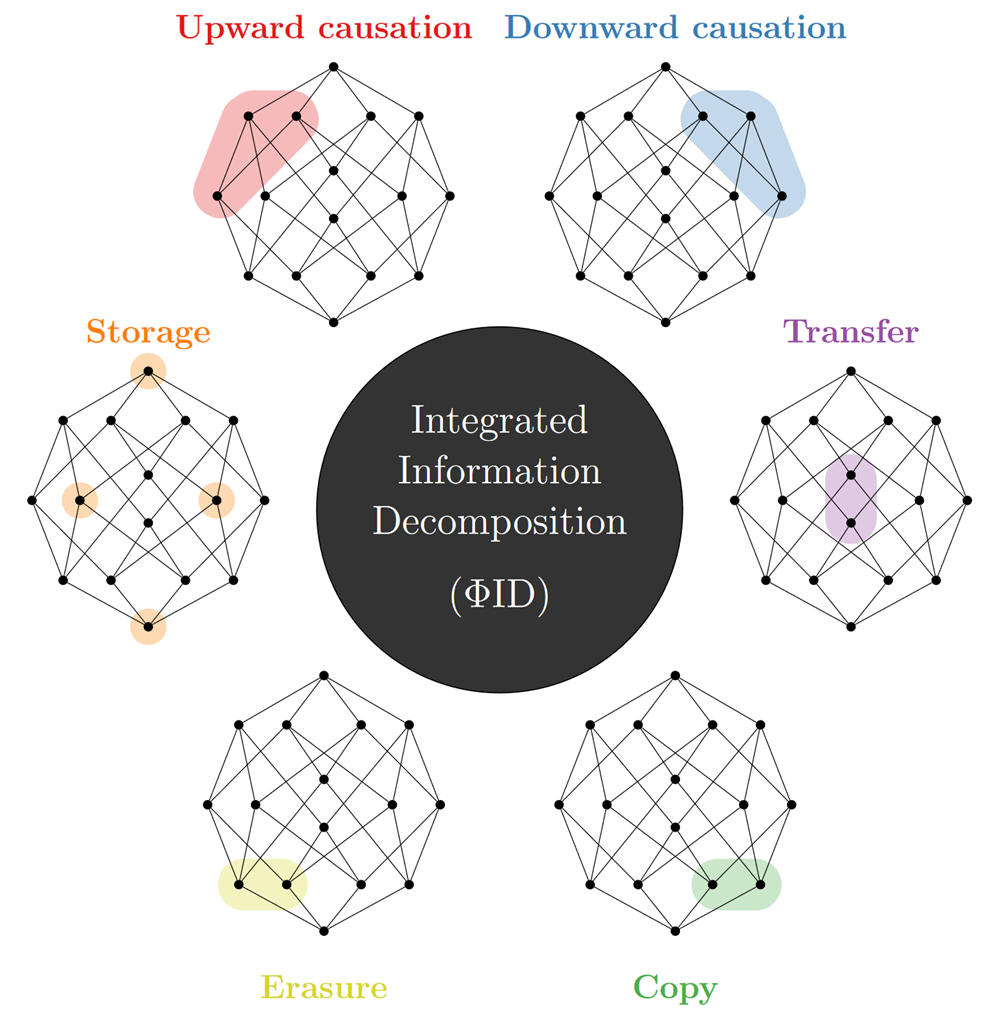
复杂系统中信息动力学的分类。六种不同的信息动力学模式，以ΦID晶格中的原子来表示。丨图片来源[7]
现在回到前面的一个问题，为什么whole-minus-sum指标算出来有时是负的？对它做一个整合信息分解就清楚了。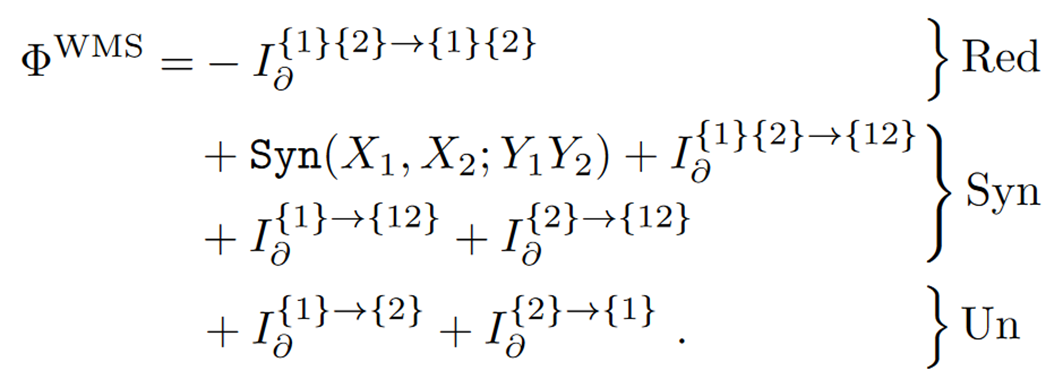

从上式不难看出，WMS有冗余、协同、特有三种类型的信息原子加和，但其中冗余信息原子前面是负号。这就意味着当一个系统冗余信息很大时，就容易出现WMS指标为负值的情况。这时候显然WMS指标不合理了，那怎么办呢？很简单，把冗余这部分去掉就好了。于是我们有了如下修正过后的WMS指标。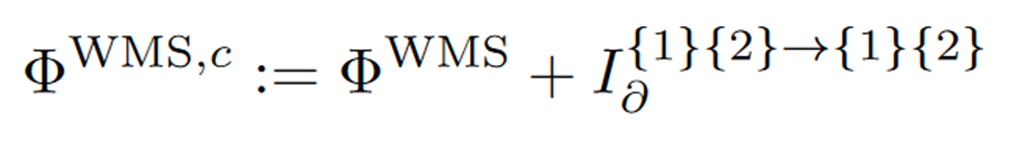

那修正后的指标好不好使呢？我们来看一个实验。下图是一个两变量的布尔网络，每一个变量按照and运算来演化，除了自身历史和另一个变量，还会受到噪音的影响。而外源的两个噪音之间是有关联的，我们可以调控这个关联程度的大小。随着关联程度增加，整个系统的整合程度会不断降低。蓝线是修正前的指标，会一直降低得到负值。而修正后的指标（红线）则会降低到0，不会出现负值。有了非负性的保障，修正后的WMS指标可以在需要度量系统整合程度的各种场合大展拳脚。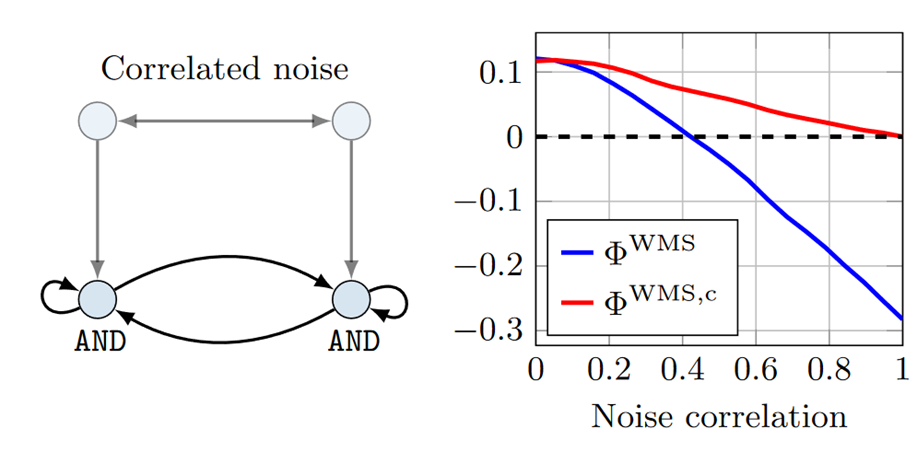
图片来源[1]
除了WMS，还有其他指标可以修正。比如因果密度（causal density）是两个方向转移熵的加和，其问题是有时会超过总的联合互信息[6]。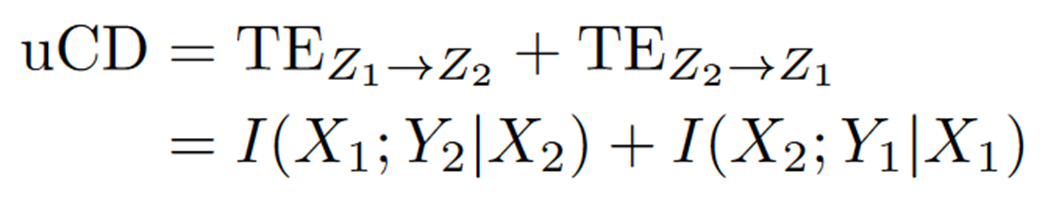

经过整合信息分解，发现这是因为其中有某一个信息原子加了两次。我们把这些经典信息论可以计算的指标都用信息原子的组合来表示，就可以画在冗余晶格上，如下图所示，其中 information storage 表示单独一个变量两个时刻之间的互信息。结合前文作者本人对信息原子的划分，我们可以重新诠释这些指标捕获的都是系统哪些方面的性质。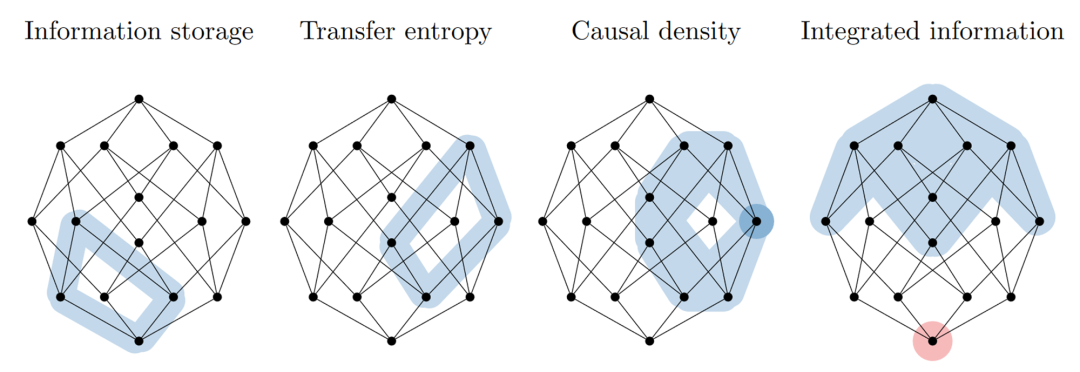
各种信息论指标的整合信息拆解，深颜色区域表示该信息原子加了两遍，红色区域表示该信息原子符号为负[7]。
各种信息论指标的整合信息拆解，深颜色区域表示该信息原子加了两遍，红色区域表示该信息原子符号为负[7]。

总结

多变量系统中的多因多果分析是一个复杂且重要的问题。复杂之处在于一个联合互信息的底层是各种信息原子的组合，而我们只有把这种宏观指标拆解到信息原子的层次才能真正理解原先指标的含义。PID框架在解决这个框架上迈出了一大步，但还不够普适，而本文提出的ΦID则将目标变量从一个延拓到多个，真正可以应用在多变量复杂系统上。进一步我们可以设想，基于该分解框架我们可以设计出度量一个系统复杂性的指标，或者至少可以重新拆解和理解已有的复杂性指标。而关于本季读书会的主题因果涌现，事实上Rosas在下一步就把ΦID应用在了因果涌现的定义和识别上，读者可以期待后续文章或读书会的解读。

参考文献主要解读论文

[1] Mediano, P. A. M., Rosas, F., Carhart-Harris, R. L., Seth, A. K., & Barrett, A. B. (2019). Beyond integrated information: A taxonomy of information dynamics phenomena (arXiv:1909.02297). arXiv. http://arxiv.org/abs/1909.02297

参考论文[2] Williams, P. L., & Beer, R. D. (2010). Nonnegative Decomposition of Multivariate Information (arXiv:1004.2515). arXiv. http://arxiv.org/abs/1004.2515[3] Lizier, J. T. (2013). The Local Information Dynamics of Distributed Computation in Complex Systems. Springer Berlin Heidelberg. https://doi.org/10.1007/978-3-642-32952-4[4] Mediano, P., Seth, A., & Barrett, A. (2018). Measuring Integrated Information: Comparison of Candidate Measures in Theory and Simulation. Entropy, 21(1), 17. https://doi.org/10.3390/e21010017[5] James, R. G., Emenheiser, J., & Crutchfield, J. P. (2018). Unique Information via Dependency Constraints (arXiv:1709.06653). arXiv. http://arxiv.org/abs/1709.06653[6] Oizumi, M., Tsuchiya, N., & Amari, S. (2016). Unified framework for information integration based on information geometry. Proceedings of the National Academy of Sciences, 113(51), 14817–14822. https://doi.org/10.1073/pnas.1603583113[7] Mediano, P. A. M., Rosas, F. E., Luppi, A. I., Carhart-Harris, R. L., Bor, D., Seth, A. K., & Barrett, A. B. (2021). Towards an extended taxonomy of information dynamics via Integrated Information Decomposition (arXiv:2109.13186). arXiv. http://arxiv.org/abs/2109.13186
相关资料推荐刘杨：整合信息分解方法https://pattern.swarma.org/study_group_issue/305

主讲人简介

杨明哲，北京师范大学系统科学学院硕士生，张江老师因果涌现研究小组成员。研究领域是因果涌现、复杂系统自动建模。学者主页：https://pattern.swarma.org/user/76769

内容大纲

• 引言

• PID介绍

• 从PID到ΦID

• ΦID中的信息原子

• 重新理解整合信息指标

• 总结

核心概念

• 部分信息分解（Partial Information Decomposition，PID）

• 整合信息分解（Integrated Information Decomposition，ΦID）

• 过剩熵（excess entropy）

• 转移熵（transfer entropy）

• 冗余晶格图（Redundancy lattice）

• 特有（Unique）

• 协同（Synergistic）

参与方式

直播信息时间：2024年1月21日（本周日）上午9:00-11:00
参与方式：

斑图链接：https://pattern.swarma.org/study_group_issue/606

扫码参与因果涌现读书会，加入群聊，获取系列读书会回看权限，加入因果涌现社区，与社区的一线科研工作者沟通交流，共同推动因果涌现这一前沿领域的发展。

新信息论：从分解到整合

因果涌现读书会第四季招募中

什么是意识？意识能否度量？机器能否产生意识？对于意识问题，人们可能即将迎来一个大的突破，各种有关意识的理论正如雨后春笋般展现出勃勃生机。其中神经科学家 Giulio Tononi 的整合信息论（IID）被认为是最有前景的意识理论之一。如果说意识是大脑神经活动的一种涌现结果，那么刻画涌现便成为理解意识过程中一个重要环节。因果涌现理论目前发展出两个派别，除了 Erik Hoel 的有效信息因果涌现框架，还有一个是 Rosas 的信息分解（PID）框架，此后 Rosas 基于此进一步提出融合整合信息论的信息分解框架 ΦID，尝试构建新的意识理论。

一边是信息整合（IIT），一边是信息分解（PID），看似分裂，实际上都是对香农经典信息论的进一步发展。因果涌现读书会第四季「新信息论：从分解到整合」由北京师范大学系统科学学院教授、集智俱乐部创始人张江老师领衔发起，旨在梳理信息论领域的发展脉络，从香农的经典信息论开始，重点关注整合信息论和信息分解这两个前沿话题，及其在交叉领域的应用。希望通过对这些“新信息论”度量指标的深入探讨，帮助我们理解什么是意识，什么是涌现，并找到不同学科，不同问题背后的统一性原理。

详情请见：新信息论：从分解到整合｜因果涌现读书会第四季启动

因果涌现社区

跨尺度、跨层次的涌现是复杂系统研究的关键问题，生命起源和意识起源这两座仰之弥高的大山是其代表。因果涌现理论、机器学习重整化技术、信息论或信息分解等近年来新兴的理论与工具，有望破解复杂系统的涌现规律。

集智俱乐部因果涌现读书会目前已经进行了三季。第一季读书会系统地梳理了因果涌现的概念，以及它与Sloopy Model、复杂性阈值、自指等概念之间的联系，也探讨了因果涌现理论在复杂网络、机器学习中的应用。参看：因果涌现读书会启动：连接因果、涌现与自指——跨尺度动力学与因果规律的探索。

第二季读书会探讨了涌现、因果科学和机器学习三大主题的融合，包括信息论拓展、因果涌现理论、因果表示学习、多尺度机器学习动力学建模。请参看：因果、涌现与机器学习：因果涌现读书会第二季启动。

第三季读书会进一步围绕因果涌现的核心问题「因果涌现的定义」以及「因果涌现的辨识」进行深入学习和讨论，对 Erik Hoel 提出的 Causal Emergence，Causal Geometry 等因果涌现的核心理论进行探讨和剖析，并详细梳理其中涉及到的方法论，包括从动力学约简、隐空间动力学学习等其他领域中学习和借鉴相关的研究思路，最后探讨因果涌现的应用，包括基于生物网络、脑网络或者涌现探测等问题展开扩展，发掘更多的实际应用场景。请参看：因果涌现读书会第三季启动：深入多尺度复杂系统核心，探索因果涌现理论应用

此次读书会主题是「新信息论：从分解到整合」，是因果涌现系列读书会的第四季，将重点梳理信息分解与整合信息论的相关研究。请参看：新信息论：从分解到整合｜因果涌现读书会第四季启动

因果涌现社区聚集了600+成员，积累了大量论文解读资料。欢迎感兴趣的朋友报名，加入因果涌现社区，解锁对应录播权限。

因果涌现读书会回放视频第一季：https://pattern.swarma.org/study_group/7第二季：https://pattern.swarma.org/study_group/16第三季：https://pattern.swarma.org/study_group/28第四季：https://pattern.swarma.org/study_group/35
因果涌现社区共创的文章

点击“阅读原文”，报名读书会