
导语
聚集活动,例如去健身房和开会,是无处不在且至关重要的传播现象,引发了高阶相互作用,因此可以被描述为高阶网络。最近,在网络科学中,揭示和理解高阶网络流行病传播的相互作用机制、时空演化模式、临界现象和相变是一个重要挑战。这篇近日发表于 Physics Reports 的综述介绍了在高阶网络上研究流行病传播动力学的最新进展,强调了统计力学和网络科学视角的贡献。文章详细介绍了单一和交互流行病传播动力学的理论方法、临界现象、相变、传播机制以及高阶网络拓扑结构的影响,并讨论了该领域的挑战和未来研究的开放问题。
研究领域:网络科学,高阶网络,流行病传播,统计力学,临界相变

朱欣怡 | 作者

论文题目:Epidemic spreading on higher-order networks
论文链接:https://www.sciencedirect.com/science/article/abs/pii/S0370157324000176
高山、沙漠、海洋、逆风,任何障碍都无法抵挡它的侵袭。
不分阶层、男女、年龄、强弱,所有人都可能受到攻击。
—— G. Wood A Treatise on the Practice of Medicine

在“您吃了吗”的问候里,病菌可能悄然传播,每一次相遇都成为潜在的传播渠道;在“您听说了吗”的分享中,信息在互联互通中如涟漪般扩散,每一次点击和分享都可能助力谣言漫天。流行病在接触网络中寻找温床,谣言在互联的纽带中找到媒介。无论是有形的病原体还是无形的思想,都在这交互的网络中扩散、延续……
流行病学建模长期以来一直吸引着来自不同领域的专家,包括数学家、流行病学家和计算机科学家。自20世纪中期以来,“数学×流行病学”领域几经扩展,产生了大量模型,这些模型经过严格的数学验证,并在实践中进行了检验,在协调、执行和评估各种预防、治疗和控制措施方面起着关键作用。这些模型构成了我们对复杂网络内传播动力学的理解的基础。
在过去的几十年里,网络科学领域涌现了大量的传播模型,关注网络的拓扑结构如何影响流行病和信息的传播。Pastor-Satorras 和 Vespignani 率先探索了无标度网络上的流行病传播[1],随后科学家们研究了不同的传播动力学(SIS/SIR)在不同的网络结构表示(多层网络,时序网络,高阶网络等)中,网络的众多拓扑特征(小世界属性,鲁棒性,社群结构)对流行病传播动力学的影响。
网络科学的进展催生了对高阶网络的研究,在高阶网络中,一条边可以连接多个节点(大于等于2),这种形式能够增强模型的表示能力,提高我们对系统演化的理解和预测。更何况,高阶交互在传播现象中无处不在且至关重要。最近 Physics Reports 上发表的最新综述,关注高阶网络上的流行病传播动力学研究的最新进展,着重介绍了统计力学和网络科学方面的贡献。这篇文章全面综述了流行病传播的理论框架、数学模型和实际应用。
文章从网络理论的基础到具体的建模和理论研究,再到未来的展望,分层次地介绍了复杂网络中流行病传播的不同方面。内容组织结构如图1所示。
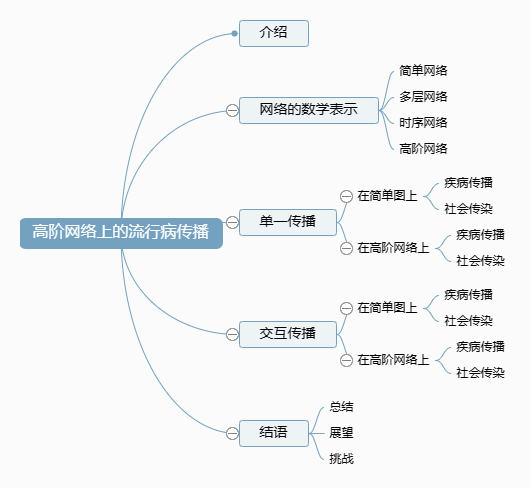
图1 综述目录组织架构图。
文章开篇介绍了对于理解复杂网络中流行病传播的研究的重要性。强调了理论研究和计算建模对于预测和干预流行病的关键性。之后简要回顾了网络科学理论,包括复杂网络理论的历史演变,从18世纪图论的发展到现代数学、计算和统计方法在研究复杂网络结构时的应用。这篇综述还为对复杂网络感兴趣的读者推荐了一些综述文章[2-4]。
为了更好地描述高阶网络上的流行病传播动力学的最新进展,第二节分别介绍了简单网络、多层网络、时序网络和高阶网络等数学工具,对这四种网络类型的适用性、数学框架和拓扑特性进行了广泛的讨论。分别从微观尺度(例如,度、权重、度分布)、中观尺度(例如,局部聚类系数)和宏观尺度(例如,平均度、介数中心性、特征向量中心性)的角度,对简单网络和高阶网络进行了系统性的回顾。
在简单网络中,实体被表示为节点,它们的交互被描绘为边。多层网络是对简单网络边类别维度的拓展,引入了不同类型的连接或关系,将网络划分为多个层次。多层网络的每个层次可以具有自己的拓扑结构和连接规则,也可以表示不同种类的关系,例如社交关系、物理距离关系、合作关系等。这种多层结构更贴近真实世界中复杂系统的互动方式,能够更全面地捕捉系统的复杂性。时序网络常用于建模和分析真实世界中随时间变化的复杂系统,是对简单网络时间维度的拓展。在时序网络中,网络的拓扑结构和连接关系可以随着时间发生变化,反映了真实系统中动态交互的特性。高阶网络进一步抽象化了简单网络中的边。在简单网络中,边表示节点之间成对的交互,一条边只能连接两个节点。而在高阶网络中,边可以表示多个节点参与的高阶交互,一条边能连接多个节点。这也是这篇综述最突出关注的差异。
在第三节和第四节,文章创新性地根据不同传播情景将流行病传播分为两种主要类型:单一传播(Single spreading)和交互传播(Interacting epidemic)。
单一传播指的是在系统中只有一种病原体或信息在传播。在这种情境下,模型关注的是单一的传染源对系统整体的影响。例如,研究一种疾病在社交网络中的传播,或者研究一个观点在社交媒体上的传播。交互传播指的是多个病原体或信息同时传播,并且它们之间可能发生相互作用。这种情境下,不同的传染源可能相互竞争、合作或产生其他形式的相互影响。例如,研究两种疾病在同一人群中的传播,或者研究两种竞争的观点在社交网络中的传播。总的来说,单一传播关注系统中单一传染源的传播动力学,而交互传播考虑了多个传染源之间的相互作用。通过阐述这两种传播模式的特征和动力学,研究者可以更好地理解流行病传播背后的机制,提供更有针对性的预防和干预策略。文章分别介绍了流行病传播和社交传播在这两种情景下的模型,重点综述了复杂高阶网络上具有代表性的流行病传播模型。
第五节对整篇综述进行了总结,强调了高阶网络研究在理解系统动力学中的重要性,展望了未来在流行病传播领域理论研究和计算建模方面的发展,并指出了一些应用上的挑战。
参考文献
[1] R. Pastor-Satorras, A. Vespignani, Epidemic spreading in scale-free networks, Phys. Rev. Lett. 86 (14) (2001) 3200–3203, http://dx.doi.org/10.1103/PhysRevLett.86.3200.
[2] S. Boccaletti, V. Latora, Y. Moreno, M. Chavez, D.U. Hwang, Complex networks: structure and dynamics, Phys. Rep. 424 (4) (2006) 175–308,http://dx.doi.org/10.1016/j.physrep.2005.10.009.
[3] R. Cohen, S. Havlin, Complex Networks: Structure, Robustness and Function, Cambridge University Press, 2010.
[4] M. Brede, Networks—an introduction. Mark E. j. newman. (2010, oxford university press), Artif. Life 18 (2) (2012) 241–242, http://dx.doi.org/10.1162/artl_r_00062.
高阶网络社区
随着对现实世界探索的不断深入,人们发现在许多真实的复杂系统中,组成系统的个体之间不仅存在二元交互关系,也广泛存在多个体同时(或以特定顺序)进行交互,即高阶交互现象。为此,研究人员分别发展出了基于超图、单纯复形、依赖关系等的网络高阶表示模型,为复杂网络分析和研究提供了新的思路。
由电子科技大学吕琳媛老师、任晓龙老师及中国地质大学(北京)管青老师在集智俱乐部联合发起了【高阶网络读书会】。读书会围绕高阶交互网络的基本概念、模型、方法与应用等研究进行研讨,按照「基础理论」+「深入理论」+「案例研讨」的模式展开。读书会第一季已经圆满结束,第二季正在筹备中。现在报名加入可以解锁第一季全部录播视频并加入社群交流。
详情请见:
推荐阅读1. 玛丽女王大学 Ginestra Bianconi:高阶网络的拓扑结构与动力学2. 高阶网络动力学综述:同步、传染、合作演化与共识形成3. Physics Reports 最新综述:高阶互动网络的结构和动力学4. 张江:第三代人工智能技术基础——从可微分编程到因果推理 | 集智学园全新课程5. 加入集智学园VIP,一次性获取集智平台所有内容资源6. 加入集智,一起复杂!
点击“阅读原文”,报名读书会




 ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง
ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง





