2024开年重磅课程：控制科学前沿理论与方法

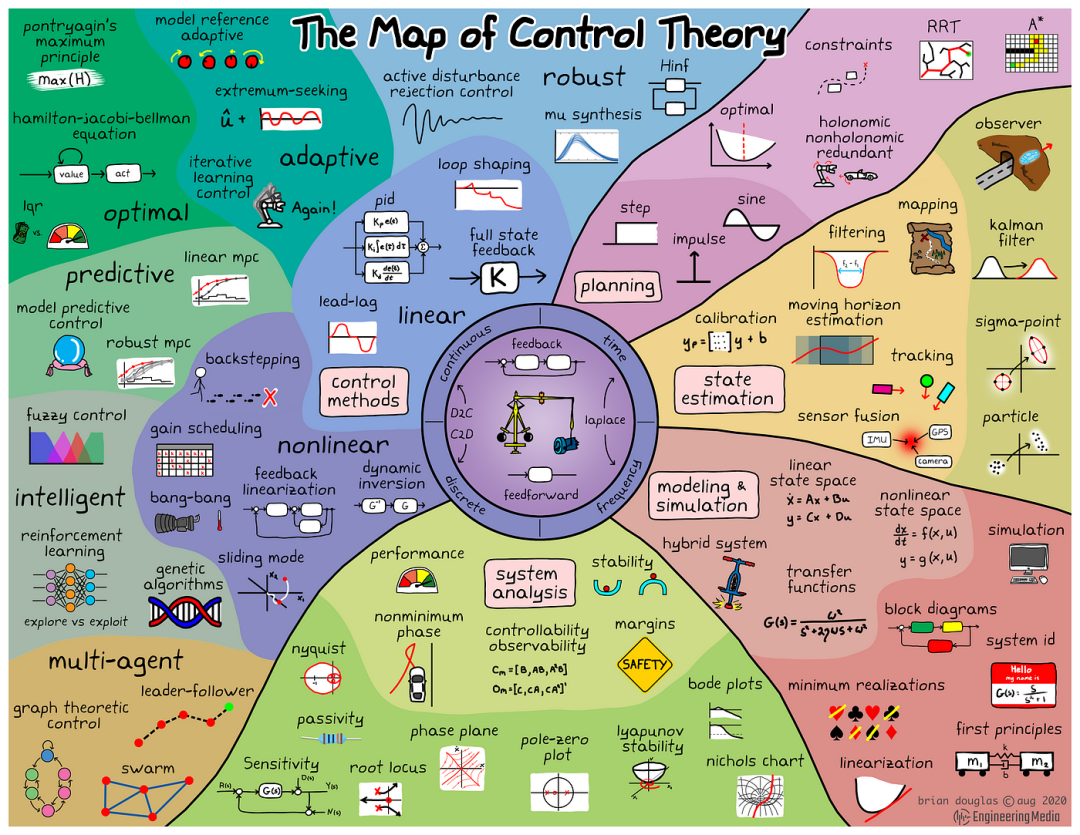
Brian Douglas绘制

系列课程引入

随着信息技术的快速发展，我们面临处理大量越来越复杂的动态系统，同时需要追求系统控制的精确性、有效性和可靠性，这带来了一系列有意义的挑战性新问题，例如如何使得控制系统对被控对象的动力学模型要有“学习”和“识别”能力，同时对环境和扰动的变化要有“适应”和“稳健”能力等，对这些新挑战的研究仍依赖于对控制领域的基本概念和基本问题的理解。
控制理论是一门高度综合、充满活力的交叉学科，处于数学、计算机科学和工程技术科学相互作用的前沿，是信息科学与系统科学的重要组成部分，同时与自然科学和管理科学的各门分支也有密切的联系。在工程、国防军事、社会、经济、生物、环境等领域复杂系统中的调控问题，发挥着重要作用。
在工程领域中，包括自动驾驶车辆的轨迹跟踪和安全控制，机器人的姿态控制和路径规划，电力系统的频率和电压稳定控制，制造过程中的质量控制和优化等；
在国防军事领域中，军事装备的导航、制导和控制，作战指挥和决策支持系统，防空导弹系统的目标追踪和拦截控制，无人系统的任务规划和协同控制等。
在社会领域中，包括交通系统的拥堵控制和信号优化，城市规划中的资源分配和城市发展控制，社交网络中的信息传播和舆论控制，疫情传播模型和防控策略的制定等；
在经济领域中，包括股票市场的交易策略和风险控制，生产计划和供应链管理中的库存控制和调度，经济政策的制定和调控，金融风险管理和投资组合优化等；
在生物领域中，包括药物输送系统的控制和释放策略，生物反应器中的生物过程控制和优化，疾病模型和治疗策略的设计，生物体内的生理调节和自适应控制等；
在环境领域中，包括污水处理厂的处理过程控制和优化，水资源管理和分配控制，空气质量监测与污染控制，天然资源的可持续利用和保护控制等。
对复杂动态系统的定量认识与科学调控，系统学与控制论是关键基础。集智学园联合中科院数学与系统科学研究院多位控制科学与工程领域专家共同开设了《控制科学前沿理论与方法》系列课程，为面向控制专业领域学生以及跨领域的学习者做深度科普，帮助学习控制论的核心思想、框架与方法。

课程框架介绍

课程时间：2024年4月2日-6月4日，每周二晚19:00-21:00

序号

时间

主讲人

主题

1

1月12日（已分享）

郭雷

系统控制之美

2

4月2日

黄一

走马观花看控制发展简史

3

4月9日

赵成

PID控制的基础理论

4

4月23日

黄一

自抗扰控制：思想、应用及理论分析

5

4月30日

李婵颖

自适应控制理论

6

5月7日

赵文虓

系统辨识

7

5月14日

赵延龙

集值系统的辨识与控制

8

5月21日

刘志新

多主体系统的分析与控制

9

5月28日

郭宝珠

分布参数系统控制

10

6月4日

齐洪胜

逻辑动态系统的分析与控制

讲师团介绍

郭雷，中国科学院院士、现任中科院数学与系统科学研究院特聘研究员、中科院国家数学与交叉科学中心主任、中科院信息技术学部主任、亚洲控制协会主席等。曾任中科院数学与系统科学研究院院长、中国工业与应用数学学会理事长、国际工业与应用数学世界大会主席、中国大百科全书（三版）系统科学卷主编等。他是中国科学院院士，发展中国家科学院院士，瑞典皇家工程科学院外籍院士，瑞典皇家理工学院（KTH）荣誉博士，美国IEEE会士，国际自动控制联合会会士，中国工业与应用数学会会士，中国自动化学会会士等。2019年他因为“在自适应控制、系统辨识、自适应信号处理、随机系统及应用数学领域的根本性和实际性贡献” 而获得IEEE控制系统学会（CSS）颁发的波德奖（Hendrik W. Bode Lecture Prize），是获此国际学术大奖的首位华人科学家。多次在控制与数学等领域国际顶级学术会议上作特邀报告。长期从事系统与控制科学研究，特别是自适应与不确定性动态系统的学习、滤波、控制与博弈等。目前研究兴趣包括：机器学习理论，自适应系统理论，智能控制系统，博弈控制系统，人机融合系统，复杂系统科学，以及在工程、社会与生命系统中相关问题交叉与应用研究。

黄一，中国科学院数学与系统科学研究院研究员，中国科学院系统控制重点实验室副主任。1989 年本科毕业于华中理工大学，1992 年硕士毕业于中国科学院系统科学研究所，1995 年博士毕业于东南大学。1995 年至1997 年在中国科学院系统科学研究所从事博士后工作，1997 年至今在中国科学院系统控制重点实验室工作，主要从事不确定系统的分析与控制研究，特别是自抗扰控制的应用及理论分析。

李婵颖，现任中国科学院数学与系统科学研究院研究员，本科毕业于四川大学数学系，获中国科学院数学与系统科学研究院硕士及博士学位。研究兴趣包括自适应控制、采样系统以及航天控制等。主持国家自然科学基金委杰出青年科学基金以及优秀青年科学基金，获第十九届中国青年女科学家奖、第四届中国工业与应用数学学会青年科技奖以及第33届中国控制会议最佳论文奖等。目前担任Automatica、Mathematical Control and Related Fields以及Journal of Systems Science and Complexity等杂志编委。

赵成，中国科学院数学与系统科学研究院助理研究员，目前研究兴趣包括不确定非线性系统控制理论及应用、随机系统控制以及PID控制理论等。入选第九届中国科协青年人才托举工程，第十五届“陈景润未来之星”等人才项目和计划，在IEEE-TAC、Automatica、中国科学：信息科学等期刊发表论文10余篇。现担任Journal of Systems Science and Complexity期刊青年编委，中国自动化学会空间无人系统自主运行技术专业委员会委员，荣获中国科学：信息科学高影响力论文、关肇直青年研究奖、中国科学院优秀博士论文以及第四届中国科协优秀科技论文等荣誉和奖项。

赵文虓，毕业于山东大学，在中国科学院数学与系统科学研究院获得博士学位，现任中国科学院数学与系统科学研究院研究员。他的研究方向主要集中在随机系统的建模、估计与控制，包括变量选择与稀疏参数辨识、随机系统的递推估计与适应控制、分布式估计与优化等。赵文虓目前担任《系统科学与数学》编委、IEEE Control Systems Letters编委，IEEE CSS Conference Editorial Board编委以及 IEEE CSS 北京分会秘书长等学术兼职，在2023获得国际自动控制联合会旗舰刊物<Automatica >的最佳论文奖。

赵延龙，中国科学院数学与系统科学研究院研究员。2002年本科毕业于山东大学，2007年博士毕业于中国科学院数学与系统科学研究院，曾先后到美国韦恩州立大学、新加坡南洋理工大学和瑞典林雪平大学等做博士后或访问交流。研究兴趣包括集值系统辨识与控制、网络通信、金融系统建模、系统生物学等，在领域内具有重要影响的期刊或会议上发表学术论文80余篇。现任SCI期刊Journal of Systems Science and Complexity负责控制领域的副主编，Automatica、SIAM Journal on Control and Optimization和IEEE Transactions on Systems, Man and Cybernetics: Systems等期刊的编委。曾任亚洲控制协会副主席，现任中国自动化学会副秘书长、中国自动化学会控制理论专委会主任等；曾获国家自然科学二等奖、中国自动化学会自然科学奖一等奖等科研奖励；先后主持国家优秀青年基金、国家杰出青年基金、中国科学院稳定支持基础研究领域青年团队计划等项目。

刘志新，2002年本科毕业于山东大学，2007年博士毕业于中科院数学与系统科学研究院并留所工作。现为中科院数学与系统科学研究院研究员，中科院系统控制重点实验室主任。曾赴美国马里兰大学帕克分校、瑞典皇家理工学院、澳大利亚新南威尔士大学等机构进行学术访问和交流。主要研究方向：群体系统分析、复杂系统控制、分布式滤波等。相关成果获美国工业与应用数学学会的旗舰期刊SIAM Review的 SIGEST论文奖、中国自动化学会自然科学一等奖、中国自动化学会青年科学家奖等奖励和荣誉。

郭宝珠，1962年2月生。1999年学院“百人工程计划”入选者 ，2003年国家杰出青年科学基金获得者， 2009年山西省首届“百人计划”专家，2013年南非科学院院士。中国科学院数学与系统科学研究院研究员、博士生导师。曾任南非金山大学(University of the  Witwatersrand计算与应用数学系讲座教授。主要从事无穷维系统的建模，控制， 数值分析，偏微分方程解的研究。研究遍及人口分布参数控制，振动系统控制分析的Riesz基理论，高维偏微分控制系统的适定性与正则性，最优控制的数值解，偏微分系统非同位镇定问题，时间延迟分布参数系统控制的镇定。过去十年，在自抗扰控制的三个主要环节：跟踪微分器、扩张状态观测器、和反馈控制给出了决定性的收敛性证明，初步奠定了这个二十多年悬而未决的控制新技术的理论基础。并推广到无穷维系统的控制，取得了极大的成功。在国际应用数学与控制理论发表期刊论文260篇以上。在Springer-Verlag 控制工程序列出版专著两本，在Wiley & Sons 出版专著一本，科学出版社现代数学丛书专著一本。数篇文章被国际同行公开称为“非常重要的文章”。所著著作被国际同行公开称为“非常重要的著作”；“引导读者进入这一非常重要的研究领域”；“足以成为应用数学专业学生的教科书或对无穷维系统分析和控制感兴趣的控制工程师和应用数学家的参考书。

齐洪胜，中国科学院数学与系统科学研究院研究员。2008年于中国科学院数学与系统科学研究院获博士学位。2008年7月至2010年6月在中科院系统控制重点实验室从事博士后研究工作。主要研究兴趣包括逻辑动态系统、博弈与控制、量子网络、分布式优化等。2011年获Automatica 2008-2010理论/方法类最佳论文奖，2012年获关肇直青年研究奖，2014年获国家自然科学二等奖（排名第二），2017年入选中国科学院青促会。已出版专著6本，发表论文80余篇。现任Journal of Systems Science and Complexity编委，中国工业与应用数学学会（CSIAM）理事兼副秘书长，中国自动化学会控制理论专业委员会（TCCT）委员。

课程简介与推荐资料

第一课：系统控制之美课程简介：“系统”是人类认识世界的基本概念，而“反馈”是调控世界、保证动态系统正常工作的基本原理，系统反馈原理既有“魅力”又有“威力”。随着现代科学技术在极端尺度与复杂系统层面的深入发展，被控系统的复杂性与控制性能的高要求，使得反馈原理将继续发挥不可替代的作用，它与“物理定律”等一样，应该受到广泛重视和应用。此外，“系统学”仍是迫切需要继续创建、深入发展的基础学科，而维纳的《控制论》所提供的丰富思想仍是今天许多学科发展的重要源泉。毫无疑问，系统控制科学的深入研究和广泛应用必将继续推动科学和技术发展、造福人类社会。在本次分享中郭雷院士将从发展历史、重要人物、核心概念、应用案例、具体方法等视角，来为我们讲述系统控制科学的魅力。本课程已于2024年1月12日分享，回放链接：https://campus.swarma.org/course/5296。
第二课：走马观花看控制发展简史课程简介：回顾控制发展简史，介绍控制课程里的一些基本概念以及判据定理等是为了解决什么问题而提出和建立的，交流历史给予的启示。推荐阅读资料：

1. Special Issue on the evolving history of control,IEEE Control Systems, 1996, 16(3)
2. Stuart Bennett. A brief history of automatic control.IEEE Control Systems, 1996, 16(3): 17-25.
3. 黄一，走马观花看控制发展简史，《系统与控制纵横》2021年第1期
4. Gene F. Franklin, J. David Powell and Abbas Emami-Naeini, 动态系统的反馈控制，电子工业出版社, 2004.
5. Richard C. Dorf and Robert H. Bishop, 现代控制系统，高等教育出版社,2001.

第三课：自适应控制理论课程简介：自适应控制的基本思想就是将系统估计与控制规律在线结合并应用到同一个反馈回路中。一个自然的并且相对简单的控制器设计方法，就是所谓的 “必然等价 (certainty equivalence)” 原则，即先假定系统结构和参数已知来设计控制律，然后，利用对结构和参数的在线估计值来代替控制器中 (未知的) 真实值。这样设计的自适应控制器未必在每一步都是最优的，因为 “分离原理” 一般不成立并且在线估计值也不一定是最好的。但是，如果随着数据的增多，由这样设计的自适应控制器能够给出渐近最优的系统性能，也就达到 “自校正” 或 “自优化” 目的了。

在自适应控制领域，利用 “必然等价” 原则设计出一个自适应控制算法一般并不困难，真正的困难在于对所设计出的控制算法，能否从理论上保证被控闭环系统具有稳定性与收敛性等所需要的良好性能。不幸的是，由于自适应控制系统的结构在本质上，是由一组很复杂的非线性与非平稳随机动态方程组所刻画 (即使被控对象是线性系统亦然)，这就使得为其建立稳定性与收敛性的数学理论带来超出预料的研究困难。

实际上，任何一个功能较为高级的 “智能化” 系统，往往都具有一定程度的 “复杂性” 的反馈结构，这似乎是 “智能化” 的必然 “代价”。但从理论研究上来讲，最容易出现下面的 “循环论证”：如果希望有满意的输出信号，就需要有满意的输入信号；但由于输入信号直接依赖于对参数或结构的估计值，因此就需要有满意的在线估计值。进一步，由于估计值又依赖于输出信号，从而需要有满意的输出信号，这又回到了论证的起点！这是理论研究中出现困难的基本原因。正因为如此，从理论上建立自适应控制系统的全局稳定性与收敛性等，被认为是这一领域的中心问题，并引起国际控制界的极大关注与广泛研究，成为现代控制理论发展史上的一个绚丽篇章。

本课程将以基于最小二乘的自校正调节器为典型代表，介绍自适应控制的基本特点、难点和成果。具体内容包括：最小二乘自校正调节器的稳定性与最优性问题以及反馈机制的最大能力与局限研究。

推荐阅读资料：

1. L.Guo and H.F.Chen,“The Astrom-Wittenmark self-tuning regulator revisited and ELS based adaptive trackers”, IEEE Trans. Automatic Control, Vol.36, No.7, July, 1991, pp.802-812 .

2. H.F.Chen and L.Guo, Identification and Stochastic Adaptive Control, Birkhauser,Boston,1991v

3. L.Guo,“Convergence and logarithm laws of self-tuning regulators”, Automatica, Vol.31, No.3, pp.435–450, 1995  

4. T. E. Duncan , L. Guo and B. Pasik-Duncan, “Adaptive continuous-time linear quadratic gaussian control”, IEEE Trans. Automatic Control, Vol.44, No.9, pp.1653-1662, September, 1999.

5. 郭雷, 回溯自校正调节器研究之路, 系统科学与数学,  32(12),1460-1471,2012.

6. 郭雷, 不确定性动态系统的估计、控制与博弈,  中国科学 : 信息科学 2020 年 第 50 卷 第 9 期 : 1327–1344

7. L. Guo, “On critical stability of discrete-time adaptive nonlinear control”, IEEE Trans. Automatic Control, Vol.42, No.11, pp.1488-1499, 1997.

8. C. Li and J. Lam, “Stabilization of discrete-time nonlinear uncertain systems by feedback based on LS algorithm,” SIAM Journal on Control and Optimization, vol. 51, no. 2, pp. 1128–1151, 2013.

9. Z. Liu and C. Li, “Is it possible to stabilize discrete-time parameterized uncertain systems growing exponentially fast?” SIAM Journal on Control and Optimization, vol. 57, no. 3, pp. 1965–1984, 2019.

第四课：PID控制的基础理论课程简介：反馈是系统控制领域的一个核心概念。在众多反馈控制算法中，具有百年历史的著名比例-积分-微分（PID）控制器是迄今为止自动控制中应用最为广泛的反馈控制方法。PID控制器具有结构简单、易于实现、不依赖被控对象具体数学模型等突出优点，它与傅里叶变换、排序算法、随机数生成等十种算法并称为“统治世界的十大算法”。长期以来在实际应用中对 PID 控制器参数的选择大多都依赖设计者的经验或实验，包括著名的 Ziegler-Nichols方法。针对 PID 控制器的理论研究大多是针对线性系统或局部线性化模型的。因此, PID的基础理论与实际应用之间存在显著鸿沟。PID 控制理论至少应该回答以下几个基本问题: PID控制在实际应用中如此成功的基本原理是什么？如何具体设计PID控制参数？PID这个线性反馈方法具有哪些局限？能否设计更为智能、可靠的PID型控制算法？本课程首先简要介绍PID控制器的发展史，通过几个案例强调其在工程系统中的地位。然后，从一类由Newton力学方程刻画的二阶非线性不确定系统出发，论证PID控制器处理这类系统的能力，阐明PID控制的跟踪性能与抗扰能力，并具体给出PID控制器参数的设计方法。最后，将简要讨论一下PID控制器具有的一些局限性，进而为工程实践人员理解PID控制器的最大能力以及进一步为克服这些局限提供理论依据和指引方向。推荐阅读资料：

1. C. Zhao and L. Guo. PID controller design for second order nonlinear uncertain systems, Science China Information Sciences, 60(2), 1-13, 2017.
2. J. Zhang and L. Guo. Theory and design of PID controller for nonlinear uncertain systems, IEEE Control Systems Letters, 3(3), pp.643 – 648, 2019.
3. C. Zhao and L. Guo. Towards a theoretical foundation of PID control for uncertain nonlinear systems, Automatica, vol. 142:110360, 2022.
4. C. Zhao and S. Yuan. Tracking performance of PID for nonlinear stochastic systems, arXiv preprint arXiv:2303.10537, 2023.
5. C. Zhao and L. Guo. Control of nonlinear uncertain systems by extended PID, IEEE Transactions on Automatic Control, 66(8), 3840-3847, 2021.
6. K.J. Astrom and T. Hagglund. PID controllers: theory, design and tuning. Research Triangle Park, NC: Instrument society of America. 1995.
7. 韩京清, 自抗扰控制技术：估计补偿不确定因素的控制技术. 北京：国防工业出版社，2008.

第五课：自抗扰控制：思想、应用及分析课程简介：自抗扰控制 (Active Disturbance Rejection Control，ADRC) 的思想和方法由中国科学院系统控制重点实验室的韩京清研究员在20世纪80-90年代提出，1998年正式以“自抗扰控制器”之名发表。ADRC 创造性地提出了“总扰动”这一新概念，“总扰动”和传统的扰动概念不同，不但包含外扰也包含系统中各处存在的参数或模型的不确定性，实现了系统内部、外部不确定性描述的有机统一，将扰动补偿和鲁棒控制融合到了一起，把控制问题的核心归结为抗扰控制问题。ADRC研究的标准态——被控量的链式积分模型精确地抽象出了运动控制系统的本质特征，自抗扰控制已在航空航天、伺服跟踪、机器人运控等领域得到了广泛的实际应用。本课程将从自抗扰控制的核心思想、应用研究及理论分析等方面进行介绍。推荐阅读资料：

1. 韩京清.自抗扰控制技术. 北京: 国防工业出版社, 2008.
2. Huang Y, Xue W. Active disturbance rejection control: methodology and theoretical analysis. ISA Transactions,2014,53:963-976.

第六课：系统辨识课程简介：系统辨识旨在根据系统的输入输出数据来建立刻画系统动态行为的数学模型，是现代控制理论中的一个分支。通过辨识建立数学模型的目的是估计表征系统行为的重要参数，建立一个能模仿真实系统行为的模型，进一步用当前可测量的系统输入和输出预测系统未来的演变以及设计控制器。通过本课程的学习，希望学生对系统辨识的形成及发展有所了解，掌握基本概念、方法、理论和分析问题、解决问题的基本技能，为从事系统控制领域的研究与应用开发打下基础。推荐阅读资料：

1. Lennart, L., System Identification: Theory for the User, Prentice-Hall, Englewood Cliffs, NJ, 1999.
2. Chen, H.F. and L. Guo, Identification and Stochastic Adaptive Control, Birkhauser, Boston, 1991.

第七课：集值系统的辨识与控制课程简介：随着信息化、大数据和智能化的发展，集值系统大量涌现，对系统建模和控制产生了新的需求。集值系统的特点是无法测得输出、状态等系统数据的精确值，只知道它是否属于某个或某些集合。例如：大量医学数据如白血病数据只知道“健康”或“疾病”，大量工程数据如卫星观测数据只知道“百米级”“千米级”等，智能决策问题如雷达目标识别关心的是目标的“真”或“伪”。与传统的精确测量系统相比，集值系统具有可利用信息少和非线性强两大特征，其辨识和控制具有本质困难，需要新的研究视角和理论方法。本课程将从几类典型的集值系统入手，介绍集值系统辨识与控制研究的特点、难点和成果，并浅谈集值系统的相关应用研究。具体内容包括：多类集值系统的参数辨识问题、集值系统的自适应跟踪控制、集值多智能体的趋同控制问题以及集值方法在复杂疾病建模、雷达目标智能识别等重要实际领域的应用研究。
推荐阅读资料：

1. Le-Yi Wang, George G. Yin, Ji-Feng Zhang and Yanlong Zhao, System Identification with Quantized Observations, Birkhauser, Boston, 2010.
2. Le-Yi Wang, Ji-Feng Zhang and George G. Yin, System identification using binary sensors, IEEE Transactions on Automatic Control, 48(11): 1892-1907, 2003.
3. Le-Yi Wang and George G. Yin, Asymptotically efficient parameter estimation using quantized output observations, Automatica, 43: 1178-1191, 2007.
4. Jin Guo and Yanlong Zhao, Recursive projection algorithm on FIR system identification with binary-valued observations, Automatica, 49(11): 3396-3401, 2013.
5. Ying Wang, Yanlong Zhao, Ji-Feng Zhang and Jin Guo, A unified identification algorithm of FIR systems based on binary observations with time-varying thresholds, Automatica, 135: 109990, 2022.
6. Lantian Zhang, Yanlong Zhao, Lei Guo, Identification and adaptation with binary-valued observations under non-persistent excitation condition, Automatica, 138: 110158, 2022.
7. Yanlong Zhao, Hang Zhang, Ting Wang and Guolian Kang, System identification under saturated precise or set-valued measurements, Science China Information Sciences, 66: 112204, 2023.
8. Jin Guo, Ji-Feng Zhang and Yanlong Zhao, Adaptive tracking control of a class of first-order systems with binary-valued observations and time-varying thresholds, IEEE Transactions on Automatic Control, 56(12): 2991-2996, 2011.
9. Ting Wang, Min Hu and Yanlong Zhao, Adaptive tracking control of FIR systems under binary-valued observations and recursive projection identification, IEEE Transactions on Systems, Man, and Cybernetics: Systems, 51(9): 5289-5299, 2021.
10. Yanlong Zhao, Ting Wang and Wenjian Bi, Consensus protocol for multi-agent systems with undirected topologies and binary-valued communications, IEEE Transactions on Automatic Control, 64(1): 206-221, 2019.
11. Ting Wang, Hang Zhang and Yanlong Zhao, Consensus of multi-agent systems under binary-valued measurements and recursive projection algorithm, IEEE Transactions on Automatic Control, 65(6): 2678-2685, 2020.
12. Ting Wang, Wenjian Bi, Yanlong Zhao and Wenchao Xue, Radar target recognition algorithm based on RCS observation sequence: Set-valued identification method, Journal of Systems Science and Complexity, 29(3): 1-16, 2016.
13. Guolian Kang, Wenjian Bi, Hang Zhang, Stanley Pounds, Cheng Cheng, Sanjay Shete, Fei Zou, Yanlong Zhao, Ji-Feng Zhang and Weihua Yue, A robust and powerful set-valued approach to rare variant association analyses of secondary traits in case-control sequencing studies, Genetics, 205(3): 1049-1062, 2017.
14. Shuping Tan, Jin Guo, Yanlong Zhao and Ji-Feng Zhang, Adaptive control with saturation-constrainted observations for drag-free satellites: A set-valued identification approach, Science China Information Sciences, 64: 202202, 2021

第八课：多主体系统的分析与控制课程简介：多主体系统广泛存在于生物、物理、化学、工程等系统中，例如鱼群、鸟群、磁化、化学组装、无人机集群等。多主体系统由多个局部相互作用的智能体组成，系统在宏观上展现单个智能体所不具备的行为、结构或功能。理解具有局部相互作用的复杂多主体系统如何涌现宏观的行为以及如何调控是是系统控制领域的根本任务。本课程针对一类典型多主体系统模型，介绍该类系统同步行为分析及调控的理论与方法。
推荐阅读资料：

1. T. Vicsek, A. Czirok, E. Jacob, I. Cohen, and O. Shochet, Novel type of phase transition in a system of self-deriven particles, Phys. Rev. Lett., 1995, 75(6): 1226–1229.

2. G.G. Tang, L. Guo, Convergence of a class of multi-agent systems in probabilistic framework, Journal of Systems Science and Complexity, Vol. 20, No. 2, pp. 173-197, June 2007.

3. Z. X. Liu and L. Guo, Synchronization of multi-agent systems without connectivity assumption, Automatica, 45(12), 2744-2754, 2009. (Regular paper)

4. G. Chen, Z. X. Liu, L. Guo, The smallest possible interaction radius for synchronization of self-propelled particles, SIAM Review, 56(3), 449-521, 2014. (Sigest paper)

5. Z. X. Liu, J. Han, X. M. Hu, The proportion of leaders needed for the expected consensus, Automatica, 47(12), 2697–2703, 2011.

6. J. Deng, L. Wang, Z. X. Liu*, Attitude synchronization and rigid formation of multiple rigid bodies over proximity networks, 125, 109388, Automatica, 2021.

第九课：分布参数系统控制理论课程简介：分布参数系统控制指的是无穷维系统的控制，主要的是由偏微分方程、泛函微分方程、积分微分方程、积分方程，Banach 或Hilbert 空间中的抽象微分方程所描述。一个房间的温度，准确的说每一点的温度都不一样，所以在任何时刻系统的状态是无穷维的。无穷是数学家在16世纪才敢面对的一个概念。在欧几里得《几何原本》里，困扰了数学家1000年的欧几里得第五公设事实上隐含无穷，因此欧几里得小心翼翼的能不用就不用。但是微积分发明以后，无穷便成了主要的研究对象。按照大数学家D.Hilbert 的观点，微积分是无穷的交响乐。数学家厉害之处在于，利用有穷的语言就可以描述清楚无穷。这是人类思想史上最伟大的飞跃。分布参数最简单的例子也许是带有时间延迟的由常微分方程描述的系统: 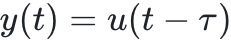 ，其中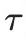>0为时间延迟， 其传递函数为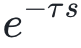，显然的这不是一个有理分式。研究这类系统的运动， 就不能在有穷维状态空间中进行。但即使是这样一个简单的分布参数系统，就和集中参数系统（用常微分方程描述的系统）有严格的区别。例如传递函数虽然在右半平面没有零点和极点，但显然的，这是一个非极小相位系统。分布参数系统之所以重要的原因是物理世界的许多现象是由偏微分程描述的。其控制问题的研究大都有强烈的实际背景。例如航天飞行器的控制振动问题由结构力学中的Euler-Bernouli方程描述 （Petrowsky方程）。工业上许多制造问题是由热传导方程描述的温度控制问题（抛物方程）；噪音控制是由声波传播的波动方程所描述（双曲方程）。此外还有流体力学中的Navier-Stokes方程，量子力学的Schrodinger方程；电磁学中的Maxwell方程等都是分布参数系统控制研究的对象。分布参数系统广泛应用于热工、化工、导弹、航天、航空、核裂、聚变等工程系统，以及生态系统、环境系统、社会系统等。在我国应用最有名的例子也许是人口问题。人口密度函数可以用一阶偏微分方程来描述，如果控制变量是总和生育率 （一个只与时间有关的控制变量， 大致描述每位妇女一生所生的孩子总数）， 就可以证明在生育年龄以内（例如60岁）的人口年龄结构是近似可控的， 但在生育年龄以外就不可控。 这个结果一方面说明我国人口政策的合理性， 但也说明仅仅调节总和生育率必然引起老龄化问题。

分布参数几乎和现代控制理论同时诞生。1954年钱学森在他的工程控制论的书中就讨论了热传导过程的分布参数系统问题，最早使用了无穷阶传递函数的概念。初期的研究受集中参数系统最优控制的Pontryagin极大值原理的启发，研究各种分布参数系统的最优控制问题。特别是法国数学家J.L.Lions的加入使得分布参数系统最优控制的研究，从泛函分析和偏微分方程的角度系统化， 抽象化。由于无穷的卷入，分布参数系统控制因此成为数学应用最多的控制分支。

本课程分为两个部分：第一部分是分布参数系统的结构理论。包括稳定性、可控性、可观性等。这些概念虽然和集中参数系统目的相同，但由于无穷的问题，很多表达并不完全等同于集中参数系统。第二部分是控制设计问题。给了一个控制问题，无论是集中参数系统还是分布参数系统，控制总要完成一些任务。在控制理论中，所有的控制任务都是通过前馈和反馈实现的。控制论关心的主要是反馈。根本的任务有三条：第一、性能输出要跟踪参考信号；第二、系统要实现内部稳定；第三、系统要抵抗干扰。

第一条很容易理解，我们难以让所有的状态依照我们的目标运转，也没有必要，改革开放有一条，就是先让少部分人先富起来。全富起来当然很好，可是一下子做不到啊。第二条就是稳定压倒一切，攘外必先安内。一个不稳定的系统指望他做事情是奢侈的。第三条最难。在实现目标的道路上不大可能一帆风顺，我们每个人都生活在不确定的世界里。但是如何对付不确定？一是把自己做的强大，这就是鲁棒控制，强者的原则。二是估计/消除不确定，这是聪明的，弱者的策略。绝大部分的人都采用估计/消除的办法生活在这个世界上。估计不确定估计的好，就有办法对付，就成功了，估计的不好，就会失败。对分布参数系统来说，控制比起集中参数来要灵活的多。有内部的控制， 集中空调就是降温的内部控制。也有边界控制，房子里需要电扇的地方吹就行了。边界控制容易实现，但带来许多数学的问题和挑战。

在课程里，虽然也讲一些抽象的概念，但我们主要的还是通过例子来说明这一切。

推荐阅读资料：

1. 分布参数系统控制，控制理论的若干瓶颈问题，第四章，44-54， 科学出版社，2002年。

2. 郭宝珠、柴树根，无穷维线性系统控制理论，科学出版社，现代数学丛书，2000

第十课：逻辑动态系统的分析与控制

课程简介：

逻辑动态系统指自变量只取有限个值的动态系统，包括2值的经典逻辑(或布尔逻辑)、k值逻辑、(一般)有限值逻辑。上个世纪末，程代展研究员提出了矩阵半张量积，打破了矩阵乘法维数限制的藩篱。近年来，以矩阵半张量积工具，给出了逻辑动态系统的代数状态空间描述方法，其关键点是将逻辑动态系统转化为用矩阵描述的离散时间系统。类似于欧氏空间上由微分或差分方程描述的动态系统的Kalman状态空间方法，它为逻辑动态系统的分析与控制设计提供了一个框架。

本课程将系统介绍基于矩阵半张量积的代数状态空间方法，然后介绍它在逻辑动态系统分析与控制理论上的应用，最后将简略介绍该方法目前在其他更多工程和理论研究领域的应用。

推荐阅读资料：

1. 程代展, 齐洪胜. 矩阵半张量积讲义 卷一: 基本理论与多线性运算, 北京: 科学出版社, 2020.

2. 程代展, 齐洪胜. 矩阵半张量积讲义 卷二: 逻辑动态系统的分析与控制, 北京: 科学出版社, 2022.

3. 程代展, 李长喜, 郝亚琦, 张潇，矩阵半张量积讲义 卷三: 有限博弈的矩阵半张量积方法, 北京: 科学出版社, 2022.

4. 程代展, 纪政平，矩阵半张量积讲义 卷四: 有限与泛维动态系统, 北京: 科学出版社, 2023.

5. 程代展, 冯俊娥, 钟江华, 吴玉虎, 张奎泽，矩阵半张量积讲义 卷五: 工程及其他系统的应用, 北京: 科学出版社, 2024. (即将出版)

课程信息

课程目的

本系列课程定位为科普课程，面向控制专业领域学生以及跨领域的学习者，会系统介绍不同控制理论背后核心的思想、框架和方法，以及重要公式的含义，培养学生对控制系统的设计、分析和实现控制的能力。通过学习这些课程，学生将了解控制论的发展历程，掌握经典和现代控制方法，探索控制系统的美妙之处。

课程适用对象

1. 对复杂系统的行为和控制机制感兴趣的跨领域研究者

2. 学习电气工程、机械工程、自动化、计算机科学等工程和科学领域的学生

3. 从事自动化与控制的工程师

对学员基础要求

本课程需要学生有一定线性代数、微积分和概率论等数学基础。

报名须知

一、参与形式

此次系列课程为周更课程，共计 10 节，从2024年4月2日起，每周二晚上7:00-9:00腾讯会议线上上课，三个工作日内上线课程录播。

课程链接：https://campus.swarma.org/course/5314

二、奖学金机制

在集智斑图网站（pattern.swarma.org）完成本课程体系下某个方向的总结文章或学习路径。经集智学园助教团队评定认可后，可作为一条贡献。一条贡献奖励400元奖学金。

可参考：

• AI何以涌现：复杂适应系统视角的ChatGPT和大语言模型

• 当机器学习遇见拓扑：拓扑数据分析与拓扑深度学习

• 探索“AI 大统一理论”：科学启发的机器学习理论

三、报名途径点击下方二维码报名加入课程：扫码报名课程请在课程详情页面，扫码二维码填写“学员登记表”，填表结束后，会弹出课程助教微信二维码，添加助教微信，即可加入课程交流群，与老师同学互动

五、课程咨询

关于课程的疑问，可以联系班主任咨询，微信：15011537754。

加入VIP，解锁集智课程&读书会

集智长期深耕复杂系统与跨学科研究，在网络科学、系统理论、混沌科学等经典领域持续策划精品课程，同时也追踪因果科学、深度学习、复杂经济学、生命复杂性、社会计算、AI+Science、大模型、神经科学、城市科学等交叉前沿。汇集了大量的探索者，包括教授、硕博、工程师、创业者等等。

为了帮助有学习需求的朋友夯实学科基础，帮有科研需求的朋友深入前沿交流，我们开放了1年制和2年制的集智学园VIP计划。VIP用户可以深度参与集智俱乐部社区，并在会员期内解锁集智学园全站课程权限。

更多关于VIP介绍，请点击查看：加入集智学园VIP，一次性获取集智平台所有内容资源

推荐阅读

1. 郭雷：以反馈控制“对付”智能时代不确定性

2. 郭雷：控制理论发展的历史启示

3. 郭雷：控制理论与技术、社会进步

4. 维纳，昔日神童和数学家丨陈关荣

5. 波德，一位现代控制理论先驱丨陈关荣

6. 苗东升：钱学森复杂性研究述评

7. 反馈：复杂系统的自我调节机制 | 集智百科

8. 《系统科学进展（第3 卷）》出版

9. 重访控制论艺术 | 复杂科学×艺术系列研讨会

10. 综述解读：经济复杂性理论及应用

11. 生物麦克斯韦妖：生命如何利用信息产生秩序

 
点击“阅读原文”，报名读书会