
01
摘要
大模型在推理任务上已经展现出了惊人的潜力,但是其多语言推理表现却十分不平衡。大模型在非英语任务上的表现往往远差于其在英语任务上的表现。出现这种情况的原因也不难理解:大模型的预训练数据和指令数据都主要由英语构成,非英语数据占比较小。因此,目前典型的解决方案是将指令数据从英语翻译到多种目标语言,然后使用多语言数据对模型进行指令微调(这种解决方案也被称为“翻译再训练”)。但是,这种方案存在两大缺陷:1)将大量指令数据翻译到多种语言造成的翻译代价大 2)在翻译形式复杂的思维链内容时难以保证翻译质量。
在本文中,我们提出了一种全新的两阶段对齐训练框架,首先利用多语言问题数据对基座模型进行微调,让其学会建立非英语问题与英语问题之间的对应关系;随后我们再借助这种建立好的针对性语言对齐,仅使用英语指令数据微调模型即可全面提升大模型的多语言推理能力。在LLaMA2-13B上的实验结果显示,我们的两阶段训练方案显著超过“翻译再训练”方案。在多语言数学推理基准数据集mGSM和mSVAMP上,我们的方案可以分别取得11.3%和16.1%的平均准确率提升。
【该工作由南京大学自然语言处理组与上海人工智能实验室,爱丁堡大学共同合作完成。本文的预印本已发布在arXiv:https://arxiv.org/pdf/2401.07817.pdf,本文相关代码已发布在Github: https://github.com/NJUNLP/QAlign,本文相关模型已开源在Huggingface: https://huggingface.co/Wenhao97】
02
训练框架
我们方案的核心思想是在使用英语指令数据微调大模型前,先利用翻译数据强化模型内部的语言对齐程度。通过这种方式,我们即可充分利用模型在英语推理任务上的出色能力来解决非英语推理任务。下面我们将介绍我们提出的两阶段对齐训练框架的具体实现方式(图1是该训练框架的示意图)。
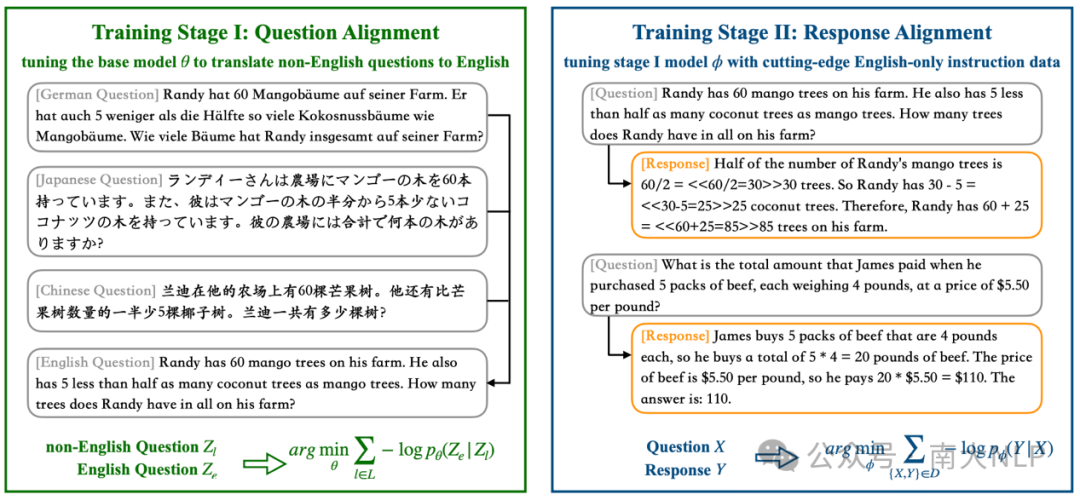 图表 1两阶段对齐训练框架示意图
图表 1两阶段对齐训练框架示意图
训练阶段一:问题对齐
此前的研究发现直接使用英文指令数据微调模型很难帮助提升模型在非英语任务上的表现 (Chen et al., 2023)。我们认为这可能是由于大模型内部不同语言未能充分对齐导致的。理想情况下,对于一个语言充分对齐的大模型,它在一种语言上的能力应该可以轻易地迁移到其他语言上。
因此,为了强化非英语与英语之间的对齐程度,我们设计了一种翻译训练任务:训练模型学习将非英语问题翻译成英语问题。具体来说,给定一组多语言问题(这些多语言问题互为翻译),那么优化目标为:
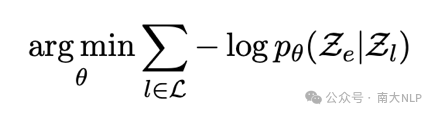
通过该阶段的训练,我们可以为大模型植入一种隐式偏好:在执行非英语任务时,自动将非英语问题与其对应的英语版本问题进行关联。值得注意的是,在该训练阶段中,我们只需要多语言问题作为训练数据,而无需多语言思维链数据。显然,相比于获得准确的多语言思维链翻译,多语言问题数据是更容易获取得到的。此外,在这个翻译训练任务中,翻译数据的类型选择也是十分重要的,翻译数据的翻译方向和数据领域都会对结果产生重大影响。在后续的实验中,我们将对这些因素进行分析,并且展示为何使用非英语到英语的问题翻译数据进行学习是该训练阶段的最优实现。
训练阶段二:答复对齐
在进行针对性的语言对齐之后,我们使用专业的英语指令数据数据来解锁模型在多语言数学推理任务上的潜能。我们考虑了两种具体的场景,分别是单语监督场景和混合监督场景。
单语监督场景:在该场景中,我们只使用英文指令数据进行答复对齐。这也是考虑到在实际中指令数据大部分都只有英文版本。在训练过程中,我们采用标准的指令微调实现方式 (Wei et al., 2022),微调语言已对齐的大模型来最大化给定问题时的答复生成概率:
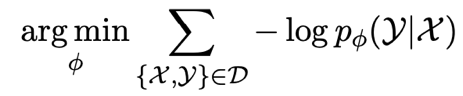
我们发现,尽管我们仅使用英文监督信号,但是却可以借助此前确立的语言对齐将模型的英语能力迁移到非英语场景。
混合监督场景:尽管我们的框架并不依赖于多语言有监督数据,但是它也可以利用额外的多语言指令数据取得更高的多语言表现。在该场景下,我们的方案是:当有一份额外的多语言指令数据时,我们先利用该数据微调第一阶段模型,再利用英文指令数据做进一步微调。实验结果表明,这种训练策略还可以进一步提升模型的多语言表现上限。
03
实验设定
基座模型:在我们的实验中,我们使用LLaMA2-7B和LLaMA2-13B这两个最强的开源模型作为基座模型,并评估了模型在以下十种语言上的表现:孟加拉语,泰语,斯瓦西里语,日语,汉语,德语,法语,俄语,西班牙语和英语。
训练数据集:在问题对齐阶段,我们采用GSM8KInstruct (Chen et al., 2023)中的多语言问题进行训练。在答复对齐阶段,我们使用最强版本的英语指令数据 MetaMathQA (Yu et al. 2023) 作为单语监督信号。在混合监督场景中,我们使用英语指令数据MetaMathQA和多语指令数据GSM8KInstruct作为监督数据(数据统计情况见表格1)。
表格 1 所涉及数据集的统计情况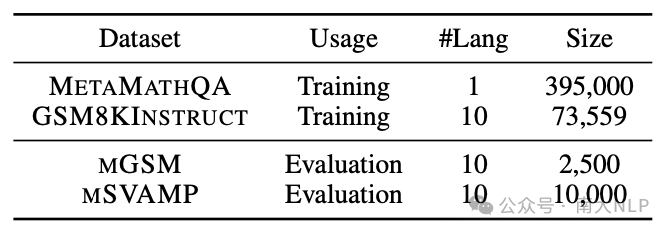
训练细节:我们在两阶段训练中都使用同一套训练超参数,都在8卡A100上进行模型参数的全量微调。训练轮数为3轮,学习率为2e-5,批大小为128。
基线系统:在实验中,我们将下列模型作为比较对象。与我们的模型一样,这些模型也是基于LLaMA2微调得到的,只是各个模型的训练方式有所不同。
–SFT (Touvron et al., 2023): 使用基础的GSM8K数据集训练得到
–RFT (Yuan et al., 2023): 使用经过拒绝采样进行数据增强的GSM8K数据集训练得到
–MAmmoTH (Yue et al., 2023): 使用GSM8K数据集和一些数学相关的指令数据集训练得到
–WizardMath (Luo et al., 2023): 在GSM8K数据集和MATH数据集上使用强化学习技术训练得到
–MathOctopus (Chen et al., 2023): 使用多语言版本GSM8K数据集训练得到,这也是“翻译在训练”方案的一篇代表性工作。我们也复现了这个模型,并在我们的实验中用MultiReason进行指代。
–MetaMath (Yu et al., 2023): 使用MetaMathQA数据集训练得到,该数据集也是目前针对数学推理任务最有效的英语指令数据集。我们复现了这个模型,在我们的实验中用MonoReason进行指代。
注意:在这些基线系统中,大部分模型使用的微调数据都只涉及英语,只有MathOctopus 和 MultiReason 是用多语言数据微调得到的。
评测数据集:我们使用多语言数学推理基线数据集mGSM评测和对比模型表现。此外,我们还使用mSVAMP数据集来评测模型在域外测试集上的鲁棒性。在下文的实验结果中,我们报告的模型表现为模型在零样本场景下的预测准确率。准确率的计算方式是比对模型答复中最后出现的数字与标准答案是否一致。
04
实验结果
额外的问题对齐阶段使得模型的英语能力能够被迁移到非英语场景:
表格2中展示了在mGSM数据集上的实验结果。可以看到,使用英语数据训练的模型 (SFT, RFT, MAmmoTH, WizardMath, MetaMath)虽然其英语表现可以不断提升,但是在非英语任务上还是表现得很一般。而使用多语言数据训练的MathOctopus模型也确实能够取得比这些模型效果更好的多语言推理表现。但是我们认为这种“翻译再训练”的范式并不是终极解决方案。因为这样翻译得到的多语言数据集十分容易过时,并且考虑到高昂的翻译代价,持续地将更新版本的英语指令数据翻译到多种目标语言也很困难。
与“翻译再训练”范式不同,我们的框架无需翻译复杂的思维链内容,只需要使用英语指令数据即可全面提升模型的多语言推理表现。从实验结果可以看出,在添加了问题对齐步骤之后 (QAlign),我们成功将模型的英语能力迁移到了非英语语言。平均来说,在7B模型上问题对齐步骤带来了11.2%的性能提升,在13B模型上问题对齐步骤带来了13.2%的性能提升。在非英语上任务上的性能提升也使得大模型在英语任务和非英语任务上的表现差距大大减小。
并且,在只使用英语指令数据微调的情况下,我们的模型也大幅超过了“翻译再训练”基线模型 (MathOctopus)。平均来说,在7B模型上提升了9.6%,在13B模型上提升了11.3%,这些结果都充分说明了我们方案的有效性。
表格 2 mGSM数据集实验结果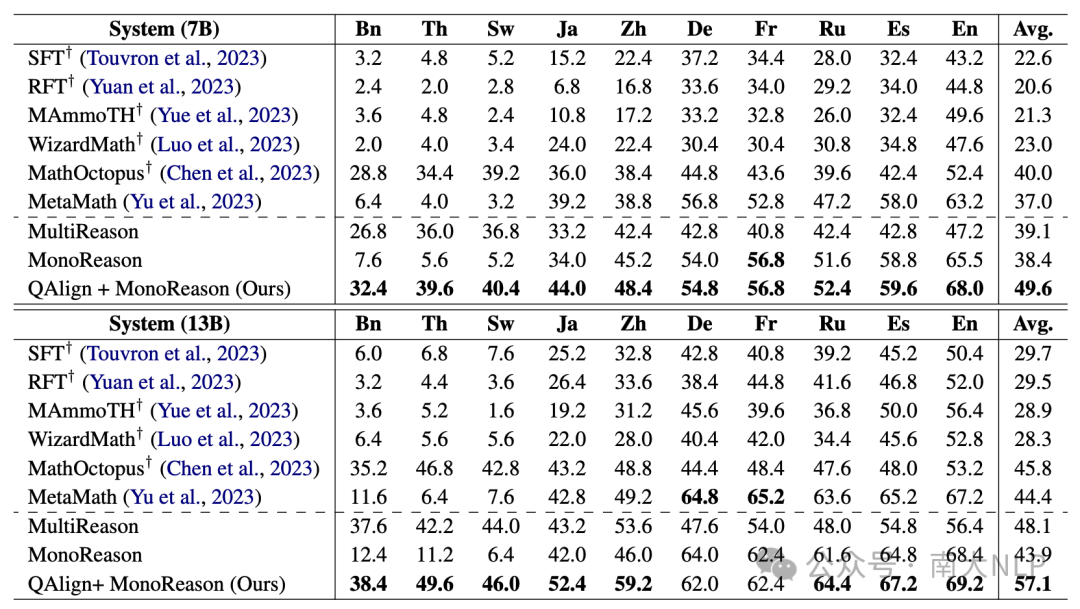
两阶段对齐框架训练得到的模型在域外测试集上也展现出了更好的泛化表现:
除了在mGSM数据集上进行实验之外,我们还在域外测试集mSVAMP上进行实验来考察模型的鲁棒性。表格3中报告了相关实验结果。总体实验现象与此前一致。额外加入的问题对齐步骤可以帮助大幅提升多语言表现,在7B模型上平均提升11.0%,在13B模型上平均提升10.8%。相比于多语言基线模型MathOctopus,我们的模型在7B规模上超过其13.2%,在13B规模上超过其16.1%。
表格 3 mSVAMP数据集实验结果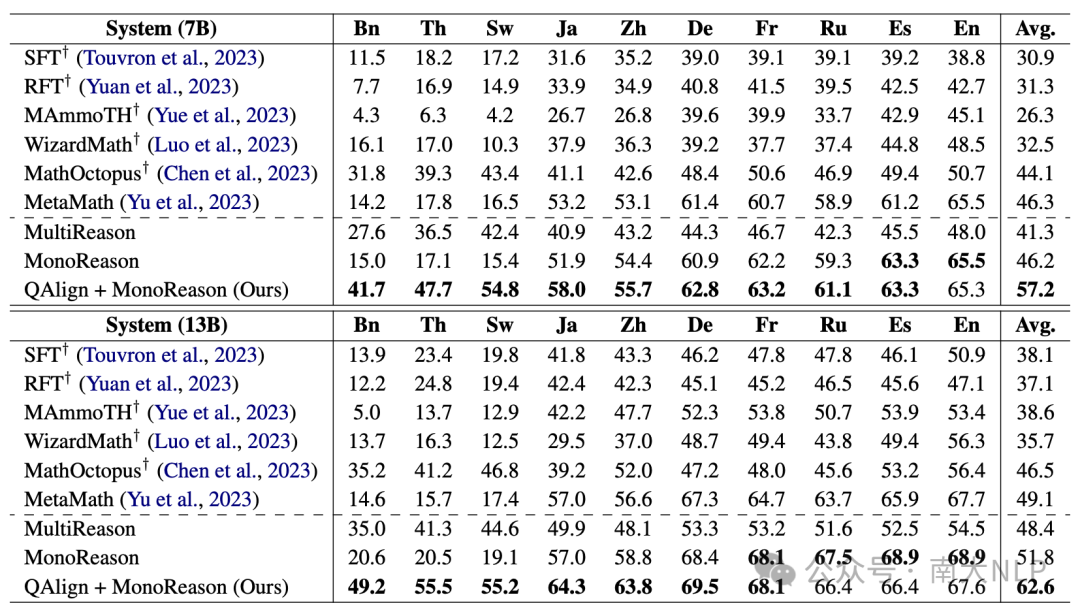
在两阶段对齐框架中加入多语言指令数据还可以进一步提升模型多语言表现上限:
尽管我们的框架并不依赖于多语言指令数据,但是当其存在时,我们也可以利用这些数据取得更好的多语言表现。在我们的实验中,我们先使用多语言数据GSM8KInstruct对一个已经进行过语言对齐的7B模型进行指令微调,再用英语指令数据MetaMathQA作进一步微调。实验结果显示(图表2)这种做法还可以进一步带来6.6%的平均多语言表现提升。
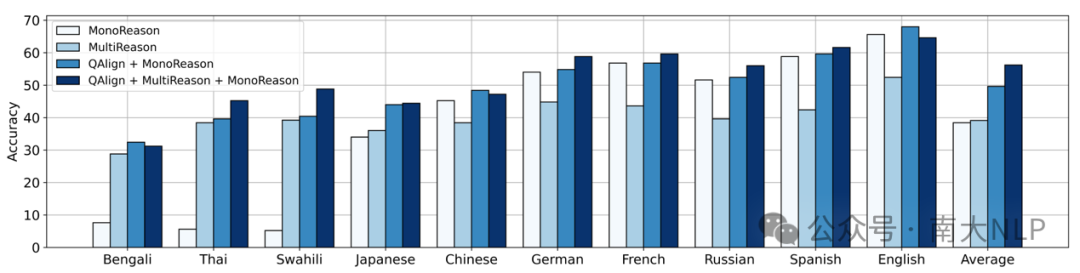 图表 2 使用混合监督数据微调模型的实验结果
图表 2 使用混合监督数据微调模型的实验结果
问题对齐阶段可以大幅提升模型的多语言预测一致性
语言对齐带来的另一个好处是改善大模型在面对多语言问题时的预测一致性。图表3展示了不同模型的预测一致性的对比结果。相比于没有进行过语言对齐的模型 (MonoReason),我们的模型 (QAlign+MonoReason) 总是可以取得更好的预测一致性。预测一致程度的改善尤其体现在一些低资源语言,比如说孟加拉语,泰语,斯瓦西里语等。
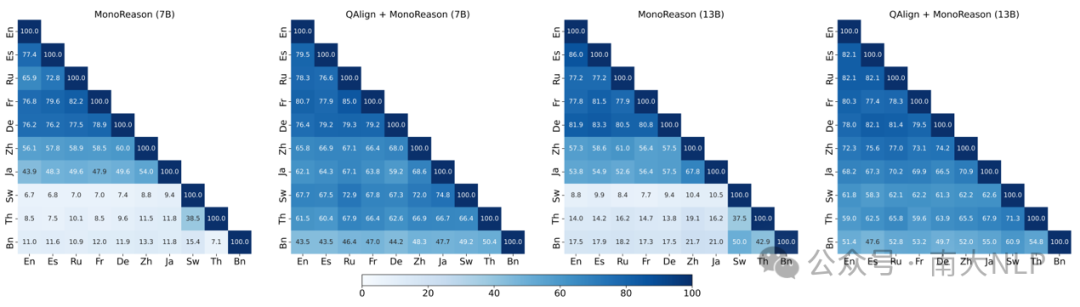
图表 3 预测一致性对比
在语言对齐阶段,翻译数据的选择至关重要:
在语言对齐阶段,我们的实现方式是训练模型将非英语问题翻译到英语。在表格4中我们进行了消融实验来展示其他实现方式的效果。我们可以看到,尽管在不同的实现方式下,模型的英语能力相似,但是不同模型的非英语表现却相差甚远。当使用反向翻译数据(从英语到非英语的问题翻译数据、从英语到非英语的答复翻译数据)训练模型时,模型的非英语表现都大打折扣。使用从非英语到英语的答复翻译数据同样也不如本文所设计的实现方式。此外,使用Flores这样的通用翻译语料训练的效果也不好,这说明翻译数据的领域也是影响语言对齐效果的一个重要因素。
表格 4 关于语言对齐阶段的消融实验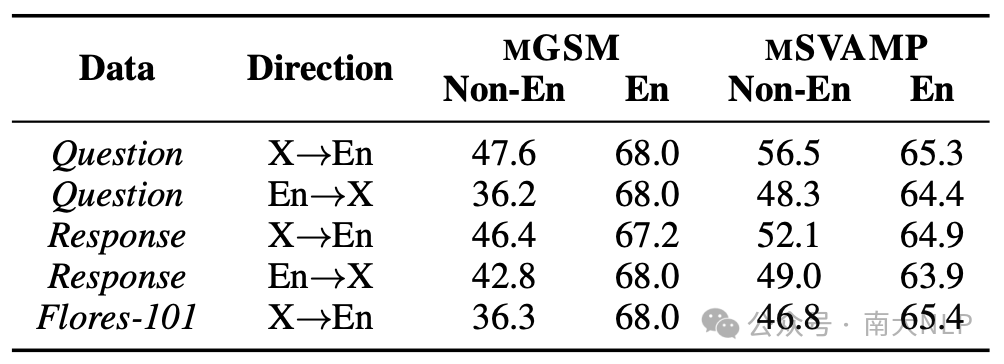
05
总结
在本文中,我们介绍了一种全新的两阶段对齐训练框架来全面提升大模型在多语言数学推理任务上的表现。在多语言基准数据集mGSM和mSVAMP上,我们提出的语言对齐技术可以帮助模型大幅超越“翻译再训练”基线 (MathOctopus),并且也可以取得更好的泛化表现。总体来说,我们设计的方案成功缩小了大模型在英语和非英语任务上的表现差距,为解锁大模型的多语言能力展现了一种新的可能。
参考文献
[1] Nuo Chen, Zinan Zheng, Ning Wu, Linjun Shou, Ming Gong, Yangqiu Song, Dongmei Zhang, and Jia Li. 2023. Breaking language barriers in multilingual mathematical reasoning: Insights and observations. arXiv preprint arXiv:2310.20246.
[2] Jason Wei, Maarten Bosma, Vincent Zhao, Kelvin Guu, Adams Wei Yu, Brian Lester, Nan Du, Andrew M Dai, and Quoc V Le. 2022a. Finetuned language models are zero-shot learners. In International Conference on Learning Representations (ICLR).
[3] Longhui Yu, Weisen Jiang, Han Shi, Jincheng Yu, Zhengying Liu, Yu Zhang, James T Kwok, Zhenguo Li, Adrian Weller, and Weiyang Liu. 2023. Metamath: Bootstrap your own mathematical ques- tions for large language models. arXiv preprint arXiv:2309.12284.
[4] Hugo Touvron, Thibaut Lavril, Gautier Izacard, Xavier Martinet, Marie-Anne Lachaux, Timothée Lacroix, Baptiste Rozière, Naman Goyal, Eric Hambro, Faisal Azhar, et al. 2023. Llama: Open and efficient foundation language models. arXiv preprint arXiv:2302.13971.
[5] Zheng Yuan, Hongyi Yuan, Chengpeng Li, Guanting Dong, Chuanqi Tan, and Chang Zhou. 2023. Scal- ing relationship on learning mathematical reasoning with large language models. arXiv preprint arXiv:2308.01825.
[6] Xiang Yue, Xingwei Qu, Ge Zhang, Yao Fu, Wenhao Huang, Huan Sun, Yu Su, and Wenhu Chen. 2023. Mammoth: Building math generalist models through hybrid instruction tuning. arXiv preprint arXiv:2309.05653.
[7] Haipeng Luo, Qingfeng Sun, Can Xu, Pu Zhao, Jianguang Lou, Chongyang Tao, Xiubo Geng, Qingwei Lin, Shifeng Chen, and Dongmei Zhang. 2023. Wizardmath: Empowering mathematical reasoning for large language models via reinforced evol-instruct. arXiv preprint arXiv:2308.09583.
[8] Karl Cobbe, Vineet Kosaraju, Mohammad Bavarian, Mark Chen, Heewoo Jun, Lukasz Kaiser, Matthias Plappert, Jerry Tworek, Jacob Hilton, Reiichiro Nakano, et al. 2021. Training verifiers to solve math word problems. arXiv preprint arXiv:2110.14168.
[9] Dan Hendrycks, Collin Burns, Saurav Kadavath, Akul Arora, Steven Basart, Eric Tang, Dawn Song, and Jacob Steinhardt. 2021. Measuring mathematical problem solving with the math dataset. In Conference on Neural Information Processing Systems (NeurIPS).
[10] Freda Shi, Mirac Suzgun, Markus Freitag, Xuezhi Wang, Suraj Srivats, Soroush Vosoughi, Hyung Won Chung, Yi Tay, Sebastian Ruder, Denny Zhou, et al. 2022. Language models are multilingual chain-of-thought reasoners. In International Conference on Learning Representations (ICLR).



 ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง
ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง


