AAAI 2024 | 重复二价拍卖中的动态预算节流方法

关键词：重复二价拍卖，预算控制，节流

导  读

本文是对 AAAI 2024 会议上发表的论文 Dynamic Budget Throttling in Repeated Second-Price Auctions 的论文解读。本论文由北京大学前沿计算研究中心邓小铁、孔雨晴课题组与腾讯广告等合作完成，邓小铁课题组博士生陈炤桦、西北大学博士生王畅与孔雨晴课题组博士生王骞为共同第一作者。论文探讨了重复二价拍卖中利用节流方法控制买家预算所能达到的表现。

← 扫码跳转论文

论文地址：

https://arxiv.org/abs/2207.04690

01

背  景

由于当前的广告拍卖市场的巨大体量、广告拍卖发生的极高频率以及广告商的优化目标和所受约束较为复杂等多方面的因素，在现在的广告拍卖市场中，广告平台往往引入自动出价代理（auto-bidder）帮助广告商进行实时报价，并在广告商所指定的约束（如预算、回报投入比等）下优化整体目标。进一步，于实际场景中，广告位的具体价值等详细信息往往由自动出价代理或其背后的广告平台预测算法直接估计；广告商由于已知信息远少于广告平台，故对广告位价值的预估往往较为粗糙。

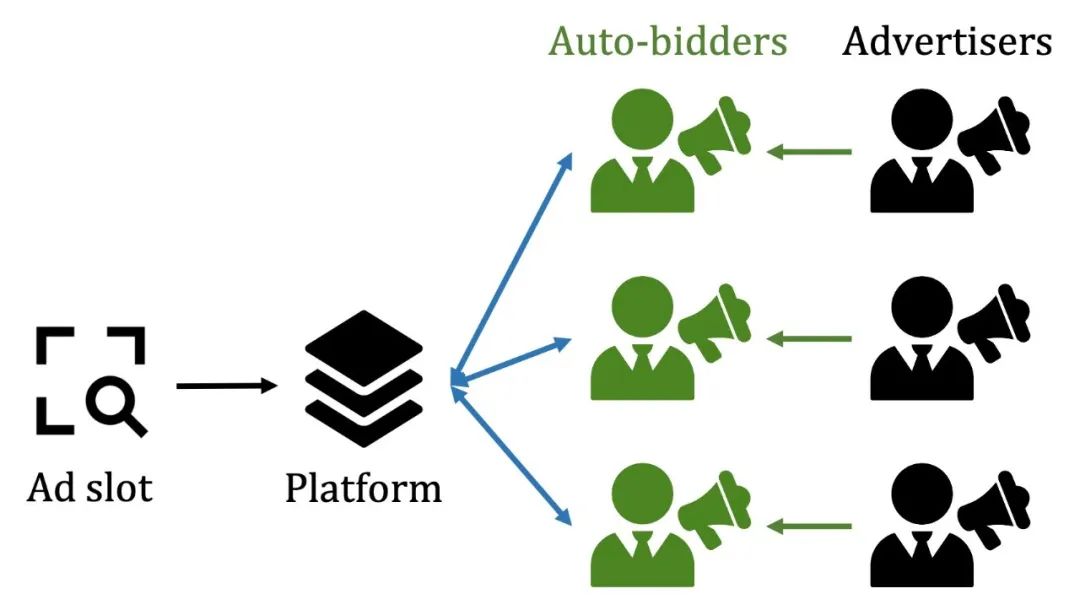
在这一背景下，我们考虑当广告商受到长期预算限制时自动出价代理在重复二价拍卖中的出价算法。受到实际业务的启发，我们特别考虑节流（throttling）算法，即自动出价代理仅能选择是否参加一场拍卖；如果参加，则其出价必须为广告位的真实预估价值。这一业务需求来源于多种原因：如，广告商不允许自动出价代理更改出价；节流策略更有利于广告商了解市场全貌等。我们主要研究节流策略所能达到的表现。

02

模  型

我们假设市场中共发生  次二价拍卖（second-price auction），其中广告商的预算为  ，  为与  无关的常数。在第  次拍卖中，广告位的预估价值为  ，这里，  可能是随机的或是对抗性的；市场中的最高竞价为  ，我们假设其独立服从于某个未知分布  。我们假设  。自动出价代理在第  次拍卖中的决策为  ；其中  代表参与拍卖，  代表不参与。我们令  ，  ，则广告商在第  次拍卖中的效益（utility）为  ，开销为  。

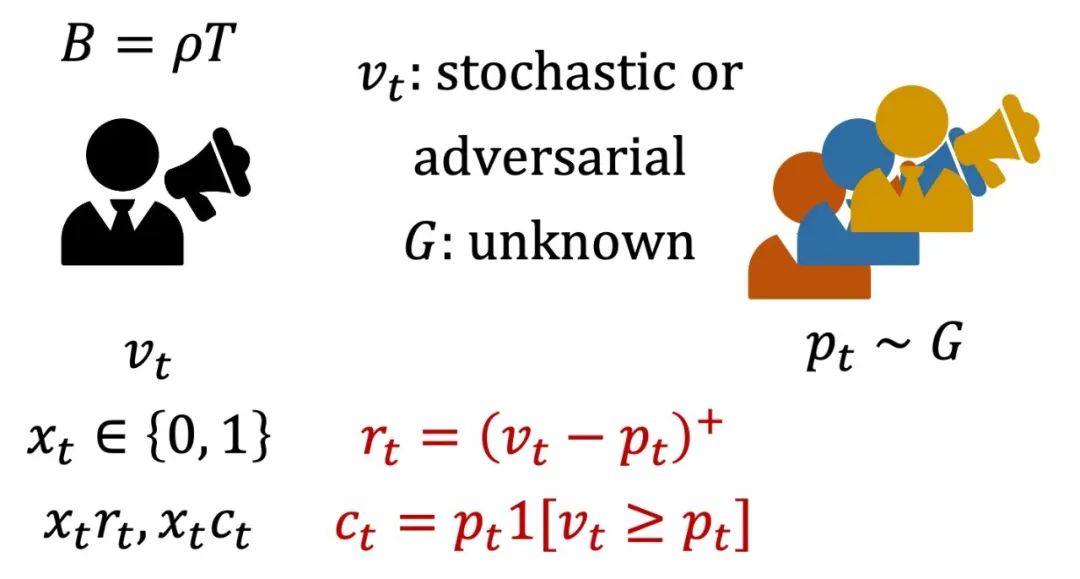
则在这一建模下，自动出价代理的优化问题为 在这一问题下，对于  是随机的或是对抗性的，我们考虑不同的评价指标。在前者情况下，我们将节流算法的效益与“流动最优”（fluid optimal）进行比较： 这里，流动最优代表着当期望意义上开销不超出预算时最优随机策略的期望效益。在后者情况下，我们则考虑“远视最优”（hindsight optimal）的期望： 

关于这两个评价指标，我们可以得到一些最优可能界和不可能结果。首先，在  随机时，存在一些实例使得任何算法的期望效益与流动最优的差（即“悔”）都是  的；其次，在  是对抗性的时，任何算法在  时的渐近竞争比（asymptotic competitive ratio）都是不超过  的。最后，我们证明了任何节流算法在面对对抗性的最高竞价  时都是无意义的；这说明了假设  随机的必要性。

03

算法结果

我们下面考虑较优的节流算法。由于最高竞价  所服从的分布  是未知的，如何获得关于  的信息尤为关键。我们这里考虑两种信息反馈模型：在全信息反馈下，自动出价代理在每一轮结束后都可以看到该轮的最高竞价；在部分信息反馈下，自动出价代理仅当参加了一轮拍卖后才能在该轮结束后看到相应的最高竞价。显然，部分信息反馈是更难处理的。

我们的工作提出了 OGD-CB 算法，其受到 [Balseiro, Lu, Mirrokni; 2023] 这一工作的启发。这一算法的关键点是动态维护一个非负标价系数  。直观地讲，由于受到预算限制，自动出价代理希望赢得那些回报投入比（即  ）较高的拍卖；而  即代表了在第  轮中期望回报  和期望开销  比值的最低阈值。当这一比值高于  时，选择参加此次拍卖；否则不参加。维护  的方法与期望开销有关：当期望开销高于  时，说明花销过大，阈值过松，故提高  ；否则说明花销过小，阈值过紧，故降低  。算法中具体更新  的方式采用了在线优化中常用的在线梯度下降（online gradient descent, OGD）方法。

当知道期望回报  和期望开销  的精确值时，上述算法当然有很好的保障。然而，由于分布  是未知的，我们只能得到这两个期望的估计值。我们的算法在这里的估计采用了置信界（confidence bound, CB）的技术。直觉上，当获得  的样本越多时，对  的估计就越准，算法效果就越好。在全信息反馈下，获取样本的频率已经达到了100%；而在部分信息反馈下，我们仍然可以证明获取样本的频率是一个常数，从而算法也能达到很好的效果。结果上，在两种信息反馈模型下，当  随机时，OGD-CB 算法的期望悔是近似最优的  ；当  对抗时，算法的渐近竞争比是最优的  。

04

节流算法与配速算法的比较

最后，我们将节流算法与配速（pacing）算法的表现进行了比较。后者是在实际业务中广泛应用的预算控制方法，其核心是将每次拍卖中的出价设置为实际价值的某一动态比值；这类算法的最优能力是不弱于节流算法的，因为节流算法是其的一个特例。

在此之上，我们证明了，当价值  随机时，在一般情况下，最优配速的期望效益是线性优于最优节流的。此外，最优配速可以应对最高竞价  对抗的情况，而最优节流不行。然而，当  对抗而  随机时，最优节流在全信息反馈或部分信息反馈下则是渐近最优的出价算法。

05

总结与展望

我们的工作提供了一个在重复二价拍卖中动态节流策略的理论全景：我们给出了最优可能界和不可能结果，给出了（近似）最优算法，同时比较了节流和配速的性能。我们还有一些尚未能解决的问题，包括证明 OGD-CB 算法是否已是最优算法，以及在老虎机（bandits）信息反馈，即仅能看到效益和花费而看不到最高竞价时分析节流算法。

参考文献：

Santiago Balseiro, Haihao Lu, Vahab Mirrokni. The Best of Many Worlds: Dual Mirror Descent for Online Allocation Problems. Operations Research, 2023.

图文 | 陈炤桦

PKU daGAME Lab

算法博弈论实验室

Distributed and Automated Games and Managerial Economics Lab

算法博弈论实验室由邓小铁教授于2019年创立，研究方向为算法博弈论、互联网和区块链经济学、多智能体及强化深度学习理论。科研兴趣聚焦在人和智能体在互联网、物联网和区块链交互环境下多方博弈的理论与方法论建立，包括数据信息的认识论刻画、均衡和动力学分析、计算复杂性和算法设计。关注计算与通讯技术兴起中应用领域的问题，特别关注互联网广告机制设计、共享经济中的激励分析和合作竞争，以及区块链的高效共识、声誉机制和跨链机制设计。

↑↑扫码转实验室主页↑↑

实验室 PI 简介：邓小铁 讲席教授

实验室相关新闻：#PKU daGAME

daGAME近期动态

• AAAI 2024 | 成对抽奖竞赛之间的竞争

• NeurIPS 2023 Spotlight | 仿射最大化拍卖机制设计的可拓展神经网络方法

• ICML 2023 | 重复二价拍卖下有预算约束的协同竞价在线算法

• ICML 2023 | 排列等价的均衡近似器的优势与局限

—   版权声明  —

本微信公众号所有内容，由北京大学前沿计算研究中心微信自身创作、收集的文字、图片和音视频资料，版权属北京大学前沿计算研究中心微信所有；从公开渠道收集、整理及授权转载的文字、图片和音视频资料，版权属原作者。本公众号内容原作者如不愿意在本号刊登内容，请及时通知本号，予以删除。

点“阅读原文”转论文链接