
导语
因果推断旨在描述给定变量之间的因果关系。然而,在许多实际系统中,变量通常只能部分观测到,而一些未观测到的变量可能携带重要信息并对目标产生因果效应。识别这些未观测到的原因仍然是一个挑战。最近这篇发表于 Entropy 「因果与复杂系统特刊」的最新研究使用一个名为神经因果信息提取器(Neural Causal Information Extractor,NCIE)的生成器-判别器框架构建隐变量,它可以补充未观测到原因的信息,从而提供包括已观测到的原因和未观察到的原因的表示在内的完整原因集合。通过最大化目标与已观察到的原因和隐变量的并集之间的互信息,生成的隐变量可以补充未观测到的原因本应提供的信息。合成实验表明,隐变量保留了未观测到的原因的信息和动力学。此外,广泛的实际时间序列预测任务在引入隐变量后显示出更高的精度,表明它们与目标之间的因果关系。本文是论文第一作者梁京昊对论文的解读。
研究领域:复杂系统,因果推断,因果图,互信息,未观测变量 梁京昊 | 作者
梁京昊 | 作者
论文题目:Neural Causal Information Extractor for Unobserved Causes
论文链接:https://www.mdpi.com/1099-4300/26/1/46
在现实场景中,通常我们研究的系统不是全部可观测的,它们包含了一些不可能或者很难观测到的变量。比如,我们很难以高时间及空间精度捕捉并建模生态系统中各种类的数量变化和环境动态;在预测空气污染程度,或者跨市交通客流量时,目前已有的数据集也很难收集到所有因变量。因变量的缺失导致无法精确描述目标变量的因果过程,也无法准确拟合预测模型。
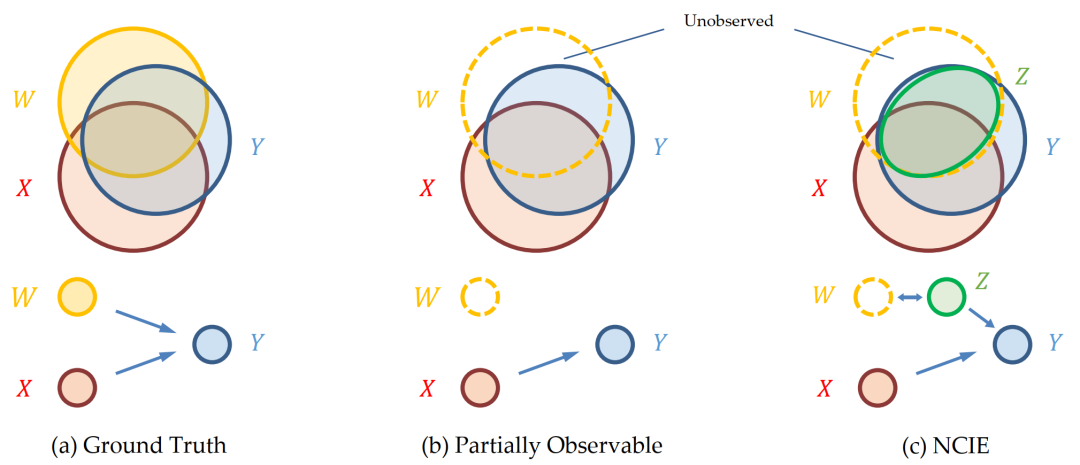
图1. 维恩图表示的信息,(a)基本事实的因果关系;(b)现实中部分可观测情景的因果关系;以及(c)由NCIE生成的隐变量Z的替代性因果关系表征,其中Y、X和W分别表示目标、观察到的原因和未观察到的原因
如图1所示,作者考虑了两个假设:1. 因变量X会给目标变量Y提供条件互信息,2. 目标变量Y的信息会被全部因变量(可观测的X和不可观测的W)的信息所覆盖。所以,在现实场景中,可观测的因变量X只能给目标变量Y提供一部分的信息,而另一部分是由未被观测的W所提供的。这篇工作的目标是生成隐变量Z,使得隐变量Z携带和表征未被观测的W的那部分信息。除了使隐变量Z表征W之外,这篇工作的另一主要贡献在于提出并实现了一种比较直接简单的利用神经网络最大化互信息和条件互信息的方法。
这篇文章会着重介绍模型的结构和它如何达成上述两个目标,并阐释此方法结构的不足之处。
研究动机
在因果推断中,隐变量或未被观测的因变量(hidden confounder or unobserved causes)是一个主要的问题,在Peter Sprites为代表的只观测不干预的因果图推断构建方法中,隐变量的问题更为严重。缺少某些变量会导致因果图上节点缺失,基于图论构建的因果图会因此有偏,画出错误的连边(因果关系)。
论文 [1] 认为,由于因果过程是一个信息转移的过程,所以目标变量的信息应由因变量提供。在时间序列中, t 时刻目标变量 Yt 的因变量包括了目标变量自身和某些其他变量的历史 ( Y<t 和 X<t)。另外,[2] 认为,任一因变量都应该给目标变量提供一些其他因变量无法提供的信息,即条件互信息 I(Yt; X<t | X<t-)。
在部分可观测系统中,本来系统中的某些因变量没有被观测到,所以已被观测的变量只能给目标变量提供部分信息。本文旨在生成隐变量,使得隐变量携带除了已被观测的变量以外的信息。具体的问题表示为:设 Yt 为目标变量, Xt 为已知变量,那么 Yt 的信息(熵)分为能被 Xt 提供和不能被提供这两部分, H(Yt) = I(Xt ; Yt) + H(Yt | Xt)。本文目标为生成隐变量 Zt 来携带 H(Yt | Xt) 这部分的信息,这可以通过 maxz I(Yt ; Zt | Xt) 来实现,因为 I(Yt ; Zt | Xt) 的上界正是 H(Yt|Xt) 。
最大化(条件)互信息
如果把 Zt 看作是 Yt 的表征变量,这个问题是一个最大化(条件)互信息的表征学习问题。最大化互信息是表征学习方法最重要的目标之一,但是如何有效且高效地衡量目标变量和其表征之间的互信息一直是个还没达致完美的问题,更别说如何最大化这两者之间的互信息。最耳熟能详的方法当属Variational AutoEncoder (VAE),通过训练代表p(z|x)的编码器encoder和p(x|z)的解码器decoder达到最大化evidence lower bound (ELBO) 的目的。这一方法能够有效地使表征携带目标的信息,但是它仍有几个限制:1. 无法处理时序数据中的时序信息,2. VAE假设表征符合高斯分布;又比如 [3] 通过数据符合高斯分布的假设能得出互信息的解析表达式,从而通过优化此表达式来最大化互信息。但是,和VAE一样,这些最大化互信息的方法都受到各种各样假设的限制,以致无法在广泛通用的情况里直接优化互信息。
有鉴于此,我们在看到了MINE [5] ,一个使用神经网络来最大化输入间的互信息的下界,从而估算互信息的框架时受到启发:既然可以利用神经网络B来最大化互信息的下界,那B的输入端既可以是某个变量,也可以是另一个神经网络A的输出。如果我们把两个神经网络A和B串联起来,可以通过优化A和B的参数,最大化某个变量 (Y) 和神经网络A的输出之间(表征)的互信息。图二为我们的框架NCIE (Neural Causal Information Extractor) 的示意图。
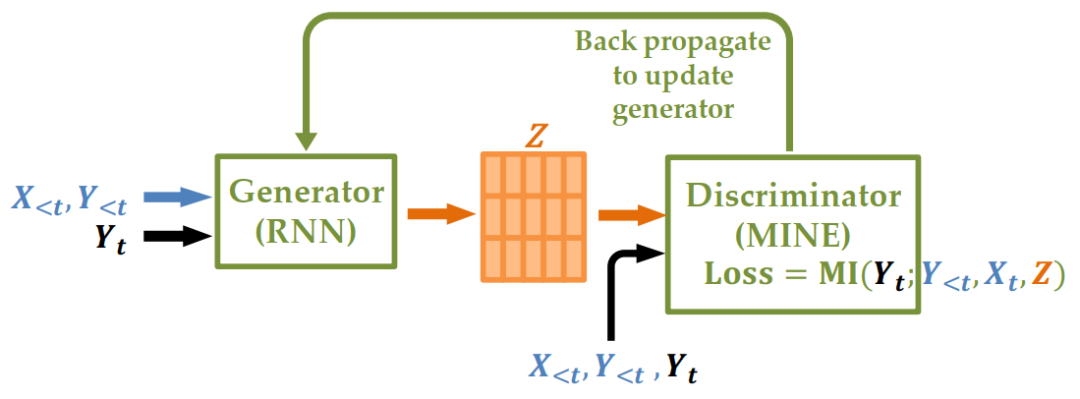
图2. Neural Causal Information Extractor(NCIE)架构
换个角度看,这其实是一个Generator-Critic(对应文章中的Generator-Discriminator)的结构:神经网络A是生成表征的Generator,而表征的损失函数,即对 Y 的互信息,则由训练好的神经网络B提供。在训练的时候,Generator会根据输入生成 Z ,而 Z 则作为Critic的输入得到Critic loss的梯度,即最大化互信息下界的梯度。这个梯度也会通过 Z 反向传播给Generator,两个神经网络的参数通过梯度下降完成更新:Critic会更准确地估计互信息,Generator生成的表征会对目标变量有更多互信息。
这个结构的优点是直接优化互信息,而且它对于数据分布的假设相对较少。这个框架比较新颖,除了这个工作之外,笔者发现同期投稿在NeurIPS,F.E.Rosas在其2023年11月发表的工作[4]也提出了相似的思路。
这个结构中的Generator和Critic也可以按需具体的问题而使用不同的神经网络。Generator可以是任何神经网络,比如CNN,RNN,LSTM等;而Critic也可以是任何能估算互信息的神经网络,比如MINE [5] 和SMILE。在这篇文章里,我们主要考虑的是从Y<t和 X<t的时序信息学习到 Zt 的表征,所以Generator使用了RNN,Critic使用了MINE。
上述的框架能生成一个表征,使得表征和目标变量的互信息 I(Y;Z) 最大化,但还没实现我们最大化条件互信息 I(Y;Z|X) 的目标。优化条件互信息要比优化互信息更困难,因为 I(Y;Z|X) = I(Z;X,Y) – I(Z;X) 需要同时最大化 I(Z;X,Y) 和最小化 I(Z;X) 这两项信息量。目前优化条件互信息的工作非常少,已经发表的文章中[6]有利用条件采样(Conditional Sampling)达到最大条件互信息,但是这种采样方式对数据的分布和它是连续还是离散有特别的要求。
虽然暂时还没有直接优化 I(Y;Z|X) 的框架,但是当我们的优化目标是对 Z 最大化 I(Y;Z|X) 时,我们发现 I(Y;Z|X) = I(Y;X,Z) – I(Y;X) 中的第二项对 Z 来说是常量,所以最大化 I(Y;X,Z) 也能达到最大化 I(Y;Z|X) 的目的。但是,这样生成的 Z 虽然能够最大化 I(Y;Z|X),我们仍无法限制 Z 是否携带了 X 的信息,这也是这篇文章还没完成的缺陷。后续我们的工作会在框架内加上一个最小化信息的模块,从 Z 中剔除 X 的信息,从而使 Z 真正的只表征 X 没有给 Y 的信息,欢迎各位老师朋友们关注我们的后续工作。
实验和结果
我们构建了几个简单的动力学系统,也采用了真实的时间序列数据集(变电器油温,跨城交通客流量,北京空气质量)来验证我们的框架。实验证明,相比单独的 X ,Z 和 X 能给 Y 提供大部分的信息。这也说明了,生成出来的 Z 能够弥补大部分 X 没有给 Y 提供的那部分信息。
此外,NCIE可以作为一个特征抽取的模块,更好的拟合和进行时间序列预测等任务。我们的实验证明,NCIE+NN,NCIE+RNN,NCIE+LSTM的预测误差要比NN,RNN,LSTM低。
作者简介

梁京昊,清华大学硕士二年级在读,目前在集智俱乐部做科研助理。研究方向:信息论,因果科学,复杂系统。欢迎有问题和讨论的老师和朋友通过邮件liangjh22@mails.tsinghua.edu.cn赐教。
参考文献
[1]Jiang, P.; Kumar, P. Information transfer from causal history in complex system dynamics. Phys. Rev. E 2019, 99, 012306.
[2]Spirtes, P.; Glymour, C.N.; Scheines, R. Causation, Prediction, and Search; MIT Press: Cambridge, MA, USA, 2000.
[3]Clark, D.; Livezey, J.; Bouchard, K. Unsupervised discovery of temporal structure in noisy data with dynamical componentsanalysis. In Proceedings of the 33rd International Conference on Neural Information Processing Systems, Vancouver, BC, Canada,8–14 December 2019.
[4]Christos, K.; Pedro M.; Fernando R. Learning Causally Emergent Representations. NeurIPS 2023 workshop: Information-Theoretic Principles in Cognitive Systems
[5] Belghazi, M.I.; Baratin, A.; Rajeswar, S.; Ozair, S.; Bengio, Y.; Courville, A.; Hjelm, R.D. Mine: Mutual information neuralestimation. arXiv 2018, arXiv:1801.04062.
[6] Wu M, Mosse M, Zhuang C, et al. Conditional negative sampling for contrastive learning of visual representations[J]. arXiv preprint arXiv:2010.02037, 2020
加入因果科学社区
随着“因果革命”在人工智能与大数据领域徐徐展开,作为连接因果科学与深度学习桥梁的因果表征学习,成为备受关注的前沿方向。以往的深度表征学习在数据降维中保留信息并过滤噪音,新兴的因果科学则形成了因果推理与发现的一系列方法。随着二者结合,因果表征学习有望催生更强大的新一代AI。
集智俱乐部组织以“因果表征学习”为主题的读书会,聚焦因果科学相关问题,共学共研相关文献。欢迎从事因果科学、人工智能与复杂系统等相关研究领域,或对因果表征学习的理论与应用感兴趣的各界朋友报名参与。集智俱乐部已经组织三季“因果科学”读书会,形成了超过千人的因果科学社区,因果表征学习读书会是其第四季,现在加入读书会即可参与因果社区各类线上线下交流合作。
详情请见:连接因果科学与深度学习的桥梁:因果表征学习读书会启动
Entropy 因果与复杂系统特刊征稿中
复杂系统无处不在。系统复杂性的一个原因是,大型系统中不同层次上广泛存在纠缠的因果结构。在复杂系统中,因果关系可能是涌现的,这意味着如果对系统进行适当的粗粒化操作,那么更强的因果关系可能只在宏观层面而不是微观层面观察得到。更进一步,自上而下的因果关系,即系统中的宏观状态变量影响微观状态变量,也可以在活系统或社会系统中观察到。
然而,我们如何从一个复杂系统的原始数据中发现这些错综复杂的因果结构并识别因果涌现,以及如何利用这些因果机制推断系统未来的状态和演化,这些都是重要而又困难的问题。机器学习、互信息分解、因果推断等新兴技术将为我们提供新的解决方案。
Entropy 杂志 Causality and Complex Systems 特刊目前在持续征稿中,欢迎对相关话题感兴趣的研究者投稿,会议文章也可投稿。
主要信息如下:
期刊:Entropy (ISSN 1099-4300)
栏目:复杂性特刊
主题:因果与复杂系统(Causality and Complex Systems)
征稿截止日期:2024年9月24日
通过以下链接进入官网查看更多信息:https://www.mdpi.com/journal/entropy/special_issues/causality_complex_systems
推荐阅读
1. 因果表征学习最新综述:连接因果科学和机器学习的桥梁2. 面向因果规律的表示学习新方法——因果表征学习最新攻略3. 图形的逻辑力量:因果图的概念及其应用4. 张江:第三代人工智能技术基础——从可微分编程到因果推理 | 集智学园全新课程5. 龙年大运起,学习正当时!解锁集智全站内容,开启新年学习计划6. 加入集智,一起复杂!
点击“阅读原文”,报名读书会





 ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง
ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง




