思维的扩散，扩散语言模型中的链式思考推理

今天为大家介绍的是来自Lingpeng Kong团队的一篇论文。扩散模型在文本处理中获得了广泛关注，与传统的自回归模型相比，它们提供了许多潜在优势。作者在这项工作中探索了扩散模型与链式思考（Chain-of-Thought, CoT）的集成，CoT是一种在自回归语言模型中提高推理能力的成熟技术。

大型语言模型（LLMs）对整个人工智能领域产生了深远的影响，转变了我们处理自然语言处理和机器学习中经典问题的方法。LLMs最显著的特点之一是它们卓越的推理能力，许多研究者认为这是LLMs带来的代表性新兴能力。链式思考提示（CoT），以自回归（AR）方式生成一系列中间推理步骤，已成为支持LLMs中复杂推理过程的核心技术。

近来，扩散模型因在视觉领域的成功和相对于自回归模型的独特建模优势而在文本处理中引起了兴趣。尽管它们尚未达到现有自回归LLMs（如GPT-4）的规模和能力，但这些模型已经展示出与GPT-2相当的性能。同时，Gulrajani & Hashimoto 强调了扩散语言模型中的规模化法则，Ye展示了扩散模型在经过指令调整和规模化后能够处理复杂任务。因此，探索以下问题变得相关重要：扩散语言模型能否也利用CoT风格的技术来获得增强的复杂推理能力？

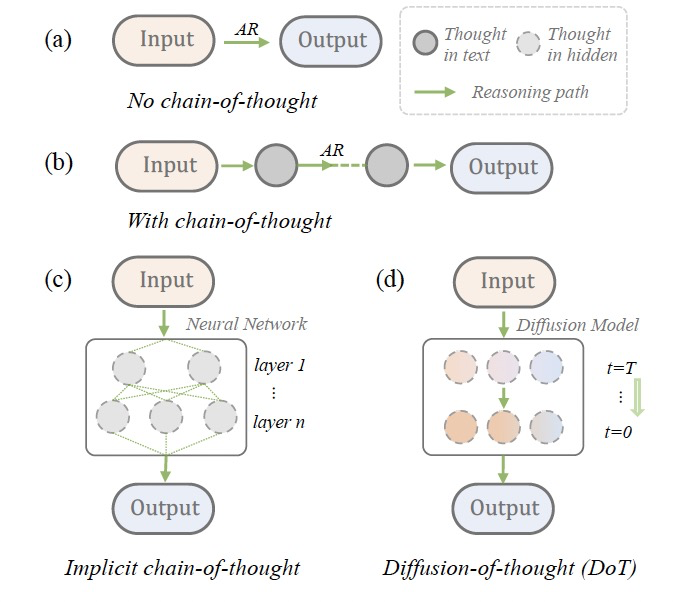
图 1

这项工作对这个问题进行了初步研究。作者提出了思维的扩散（DoT），一种为扩散模型量身定制的固有链式思考方法。本质上，DoT逐渐更新表示隐藏空间中思维的一系列潜变量，允许推理步骤随时间扩散。从方法论角度来看，DoT与最近提出的隐式CoT方法有相似之处，后者通过跨transformer层学习隐藏状态中的思维，以提高自回归CoT生成的时间效率。CoT、隐式CoT和DoT的示意图可以在图1中找到。在实践中，DoT在每个扩散时间步t迭代地对数据点施加高斯噪声，其中t从t = 0（最少噪声）运行到t = T（最多噪声），然后训练去噪模型从噪声数据中恢复干净数据。为了针对复杂查询，DoT不使用基于梯度的分类器引导，而是使用无分类器引导训练和采样去噪模型，以提供更可靠的控制信号。

方法

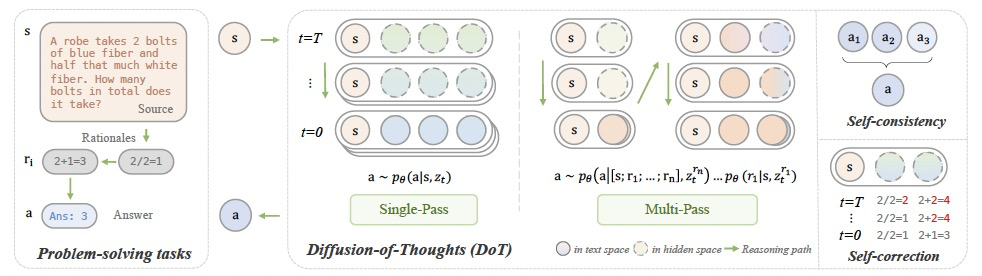
图 2

DOT的流程如图2所示。受到扩散模型在文本生成中成功的启发，作者探索它们在特定任务中的推理能力及其相对于自回归模型的潜在优势。作者首先观察到Plaid模型中默认的基于梯度的引导无法进行精确的条件设置，因为模型不能完全恢复每个条件token。这在数学推理中尤其重要，因为它期望基于问题陈述中的确切token（例如，数字）进行推理，而不是更紧凑的梯度信号。为此，作者在Plaid的微调过程中采用了DiffuSeq风格的无分类器条件设置。这产生了DoT的原型，其中所有的推断都是通过一次性的逆向扩散过程生成的，所有条件token都被固定。具体来说，在训练和采样过程中，问题上下文与理由（链式思考推理路径）z0 = EMB([s; r1…n])被串联起来，且部分噪声仅施加于理由部分zt，保持s作为条件锚定。通过多步去噪过程DoT从扩散模型的内在自我修正能力中受益。为了进一步提高自我修正能力，作者设计了一个计划采样机制使得在训练阶段暴露并纠正自生成的错误思维。具体地，对于任何连续的时间步s, t, u，满足0 < s < t < u < 1，在训练阶段zt是从q (zt | z0)中采样的，而在推理过程中则是从q(zt | fθ (zu; u))中采样的，其中fθ是一个重新参数化Eq[z0|zt]的去噪神经网络。这种暴露偏差可能会阻碍模型在生成过程中从错误思维中恢复，因为模型fθ只在从标准数据扩散的zt上训练。为了缓解这个问题，对于时间步t，作者随机采样一个之前的连续时间步u ∈ (t, 1]，并执行模型前向传递以获得预测的z0。然后采样zt以替换损失计算中的常规值。与自回归模型的计划采样相比，DoT中的这种机制帮助模型考虑全局信息从错误中恢复。

作者进一步提出了DoT的多通道（MP）变体，称为DoTMP，该变体以一个接一个的思维范式生成理由。这种方法分离了多个理由的生成，并引入了因果归纳偏差，使得后续的理由可以在生成过程中被先前理由的更强条件信号所引导。具体来说，在第一轮中，作者通过模型生成第一个理由r1。然后将r1与s作为条件[s; r1]连接起来，通过模型采样得到r2。通过多次迭代，可以得到最终答案。

实验部分

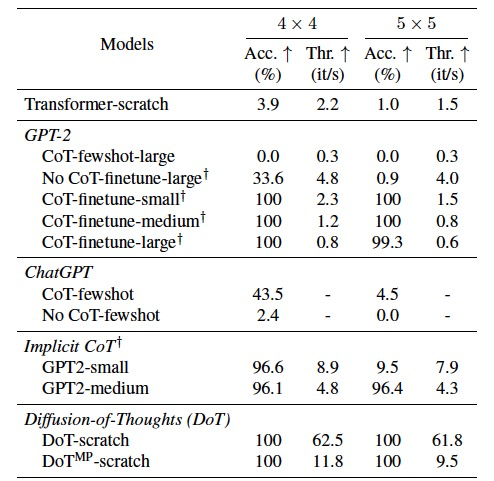
表1

作者首先从头开始训练DoT以完成数字乘法任务作为初步调查，如表1所示。可以观察到，ChatGPT和精简版的隐式CoT模型都无法达到100%的准确率。GPT-2可以通过微调达到高准确率，但在CoT过程中牺牲了吞吐量。有趣的是，从头开始训练的DoT能够在将扩散采样步骤设置为1的情况下，保持显著的吞吐量同时达到100%的准确率。随后作者从头开始在GSM8K上训练DoT，但只能达到5.61%的准确率，这低于GPT-2的微调版本。作者认为，这主要是由于从头开始训练DoT时缺乏预训练的自然语言理解能力。这就是为什么作者开始通过使用预训练的扩散模型进行进一步的微调探索。

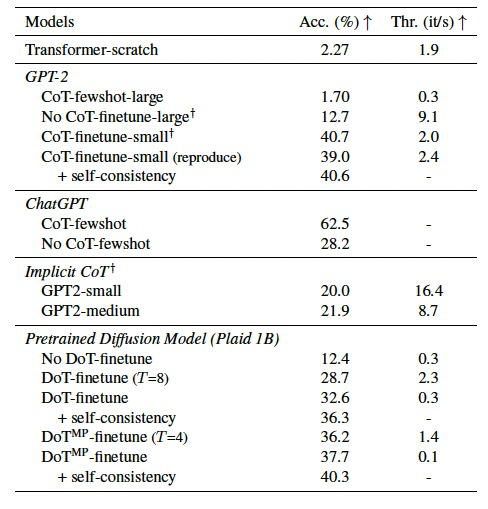
表 2

作者将DoT扩展到预训练的扩散语言模型Plaid 1B并在更复杂的推理任务上进行评估，即GSM8K。在表2中，与不使用CoT/DoT相比，自回归模型和扩散模型在使用CoT或DoT进行微调时都显示出显著提高的性能。这表明增加的计算（推理时间）带来了实质性的好处。DoT，与隐式CoT有类似的公式，但展现出比它更显著增强的推理能力，可与微调CoT模型的GPT-2相媲美。多通道DoT表现略优于单通道版本，而后者更高效。

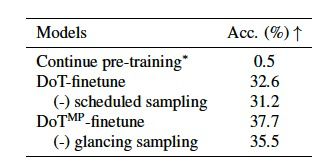
表 3

在微调Plaid 1B时，作者探索了几种替代方案并进行了如表3所示的消融研究。使用GSM8K增强数据集继续预训练Plaid 1B并使用基于梯度的条件进行推理，对于在下游任务上微调扩散LM来说不是一个好选择，因为推理任务需要更具体的指导。

编译 | 曾全晨

审稿 | 王建民

参考资料

Ye, J., Gong, S., Chen, L., Zheng, L., Gao, J., Shi, H., … & Kong, L. (2024). Diffusion of Thoughts: Chain-of-Thought Reasoning in Diffusion Language Models. arXiv preprint arXiv:2402.0775