诺奖得主丹尼尔·卡尼曼：如何获得幸福？

认知心理学家，2002年诺贝尔经济学奖得主丹尼尔·卡尼曼（Daniel Kahneman，1934年-2024年3月27日）, Photo: Denise Applewhite, Princeton University, Office of Communications.

编者按

2024年3月27日，美国认知心理学家丹尼尔·卡尼曼（Daniel Kahneman）去世，享年90岁。他因“将心理学研究的见解融入到经济科学中，特别是在不确定性下的人类判断和决策方面”而获得 2002年的诺贝尔经济学奖。丹尼尔·卡尼曼发现，人们常常依赖思维捷径，这常常导致他们做出违背自身最佳利益的错误决定。
生前，卡尼曼曾为Frontiers for Young Minds杂志撰文，介绍自己在行为经济学领域的研究，并向小读者分享了对于如何获得幸福的感悟。他指出，世界上有两种类型的幸福：在生活中感到幸福，以及对人生感到幸福满足。卡尼曼建议，我们应该思考以下两个问题：你更乐意怎样度过每一天？你的人生目标是什么？对于这两个问题的回答和关注，将影响到个体的幸福感。
研究领域：行为经济学，前景理论Daniel Kahneman | 撰文胡唐燕 | 翻译玛雅蓝 | 校译

人类行为复杂多样，是一种十分有趣的现象。尽管任意两个人的行为之间都存在许多差异，但我们可以在不同情境中发现一些典型的行为模式，比如在教室里或家庭聚餐时。行为经济学领域研究的是与财务状况相关的行为。在本文中，我将介绍前景理论的主要发现，这一理论由已故的阿莫斯·特沃斯基 (Amos Tversky) 和我共同提出。前景理论解释了在涉及赌博的情境下人们做出的决策，同时也回答了一些问题，比如人们是否以同样的方式评估收益和损失，或一个人的初始财务状况如何影响其对收益和损失的估值。在文章的最后，我将分享我在科学生涯中得到的一些感悟，并解释为何幸福具有两个面向。

前景理论

想象一下，你的朋友邀请你玩下面这个游戏：她负责抛硬币，你来猜测硬币落下后哪一面朝上。如果硬币正面朝上，你就得到3元；如果反面朝上，你就输掉3元。在这种情况下，收益和损失一样多，并且两种结果发生的概率都是50%，因为硬币只有两个面。你会选择玩这个游戏吗？再假如你的朋友改变了游戏规则，硬币正面朝上则你得到5元，反面朝上则你输掉3元呢？在这种情况下，收益和损失的金额是不一样的，但每种结果发生的概率还是50%（如图1）。

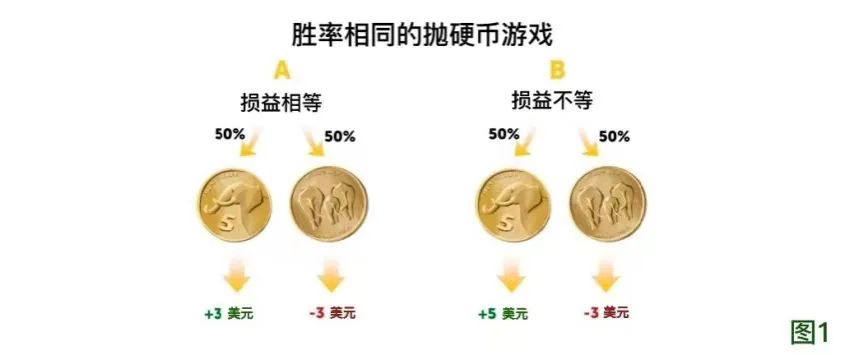图1 有得有失的抛硬币游戏。（A）胜率相等（50%）、损益也相等的赌博。硬币正面朝上则得到3元，反面朝上则失去3元。你会选择玩这个游戏吗？（B）胜率相等（50%）但损益不等的赌博。硬币正面朝上则得到5元，反面朝上则失去3元。你会选择玩这个游戏吗？

再来想象一下，你的朋友邀请你玩另一个游戏：她来掷一个普通的六面骰子。假如她掷出1至4点中的任意点数，你就得到3元；假如她掷出5点或6点，你就输掉3元。在这种情况下，你的收益和损失一样多，但是输赢的概率不一样：赢的概率是66%，而输的概率是33%。你会选择玩这个游戏吗（如图2）？

图2 损益相同但胜率不同的掷骰子游戏。在本游戏中，掷出1-4点中的任意点数，则得到3元（如左图）；掷出5点或6点，则失去3元（如右图）。你愿意玩这个游戏吗？

这都是一些简单的赌博游戏，损失和收益情况各不相同。现在，再请你想象一下你肯定能盈利，只是收益金额不同的游戏情境。例如，如果有人让你选择肯定能得到3元，或有80%概率能得到6元，你会选哪个呢？或者换一种情形，如果在马上得到3元和两周后得到10元之间做一个选择的话，你又会选哪个呢？
前景理论研究的就是上述情况，由我已故的好友阿莫斯·特沃斯基和我共同提出。前景理论是一个行为经济学理论，研究人们在不确定的情境下（比如赌博时）做出的决策[1-3]，旨在解释人们做决策的原因和方式。在下文中，我将介绍前景理论的两个主要发现，并解释它们的含义和与上述情境的关联。

人们赌博的时候在想什么？

过去的观点认为，在考虑风险决策的结果时，人们都会估量输赢对财务状况产生的影响。例如，一位商人要把货物（如香水）从阿姆斯特丹用船运往圣彼得堡，他知道这艘船有5%的概率在途中沉没，无法到达目的地。因此，这位商人面临两种选择。第一，这艘船有95%的可能性安全到达目的地，在这种情况下，他就可以卖出香水，获得预期利润。
第二，这艘船也有5%的可能性在途中沉没，这样的话商人花在香水上的钱都会赔光。因此，商人需要决定是否为船上的货物投保。他应该选择投保，在船沉没后获得跟香水成本相当的赔偿，还是选择不投保，赌一把，希望船能安全抵达呢？
著名科学家丹尼尔·伯努利（Daniel Bernoulli，1700-1782）研究过这一问题，他认为人们会考虑资产的未来状态。也就是说，人们在做经济决策（如赌博）时，评估的是输赢分别会使自己处于怎样的财务状况。关于这一点，我和阿莫斯·特沃斯基或许有发言权。我们注意到，对于日常生活中的风险决策（通常不涉及上文所述船只那样的大额风险交易），人们考虑的是收益和损失，而不是不同的结果将使他们处于怎样的财务状况[2-4]。回想一下上文提到的游戏：当你选择是否参与赌博时，你可能会考虑如果赢了会得到多少钱，如果输了会失去多少钱。你很可能不会考虑在两种情况下你口袋里钱的总量的变化情况。换句话说，人们关注的是赌博给财务状况带来的变化。这种情形一般用一种曲线图来表示，称为价值函数（如图3）。这些变化是相对于下注前的个人财务状况（被称为“零状态”）来衡量的，即图3中坐标轴原点的0。

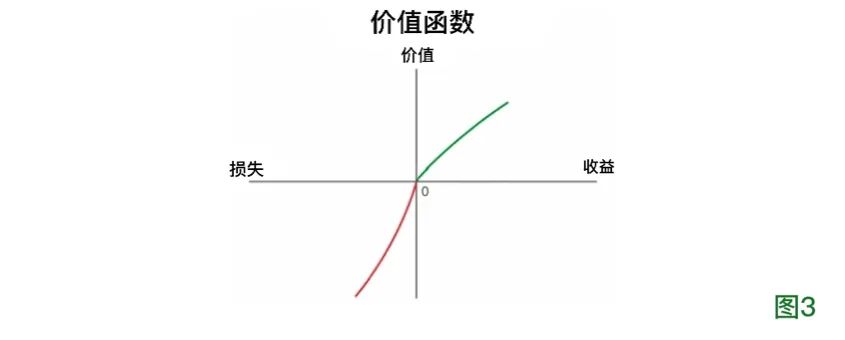
图3 价值函数图表。前景理论的一项重大创新，就是从强调赌徒在完成下注后的最终财务状况，转向强调相对于赌徒下注前的初始财务状况的收益与损失（横轴）。初始财务状况用坐标轴的原点（0）表示，收益或损失是相对原点来衡量的，并与下注人的主观价值（纵轴）相关。每个人自行判断收益对他们有多重要，以及损失对他们的“伤害”有多大。前景理论认为，损失造成的心理伤害要大于等量收益带来的喜悦（红色曲线比绿色曲线更陡峭）。（图片改编自参考文献2。）

损失厌恶

既然认识到问题的关键在于赌徒财务状况的变化，我们就有了这样的疑问：对赌徒来说，收益和损失是否具有同等的重要性？再来回顾一下图1的游戏。在第一个版本里，胜率相同，收益和损失一样多，这种赌博人们并不喜欢。人们更喜欢第二个版本的赌博，收益的价值高于损失的价值，且胜率相同。换句话说，为了“补偿”损失带来的风险，需要更大的潜在收益。由此可以得出一个重要结论：人们对待收益和损失的态度是不对等的。人们对损失的厌恶超过了对收益的渴望，我们将这种现象称为损失厌恶。[5]
图3形象地描述了损失厌恶。图中右侧的绿色曲线代表人们赋予收益的价值，左侧红色的曲线与之形成对照，代表人们赋予损失的价值。从图中可以看出，收益曲线上升得更慢、更平缓，损失曲线则更陡峭。也就是说，面对实际价值相同的收益和损失（比如得到3元和失去3元），人们对损失的消极体验会超过对收益的积极体验。
你可以自己做一个测试：得到3元的兴奋能盖过失去3元的难过吗？大多数人都会说，失去3元的沮丧远远甚于得到3元的喜悦。这种人类特征在许多文化中都有体现，我们相信它有进化的基础（挑战：从进化的角度来看，你能想想这种对损失更加厌恶的特征如何服务于人类吗？）。值得注意的是，尽管在我们的研究之后，人们对损失规避现象的认识有所增加，但这种心理并未减弱。不过，这些研究让我们能够理解人们在经济决策情境下的行为，这是以往的理论无法解释的。

给小读者们的建议

• 幸福的两个面向

最后，我想和大家分享一些我研究生涯中的重要见解，这些见解与经济学并无直接关系。第一个见解来自行为心理学，源自一个问题：“什么使人快乐？”另一个见解来自我作为一名科学家对自己的观察。
对每个人来说，幸福都是富有意义而又难以捉摸的。每个人通往幸福的路径都不一样，取决于很多因素。尽管如此，你应该认识到世界上有两种类型的幸福——在生活中感到幸福，以及对人生感到幸福满足（如图4）[6-7]。在生活中感到幸福也叫做即时幸福感，它与生活中的瞬时体验有关，例如：做自己开心吗？我在当下的感受如何？这种幸福与我们的心情紧密相关。事实证明，平均而言，人们最快乐的时候就是与所爱之人和爱他们的人共度的时光。
而对人生感到幸福满足也称为生活满意度，与对生活的总体态度有关，例如：我过得成功吗？我为自己所获得的成就感到自豪吗？换言之，满意度取决于你认为过往的生活各方面是成功还是失败。
因此，我的建议是，应该思考幸福的两个面向：你更乐意怎样度过每一天（在生活中感到幸福）？你的人生目标是什么（对人生感到幸福满足）？这两个方面不总是齐头并进的，但如果能同时关注到这两方面，那你获得这两方面幸福的概率就会增加。另外还要注意的是，我们在其他研究中发现，财富与幸福之间的关系并不像人们想象的那样简单明了[8]。因此，为了获得幸福，我建议不要把注意力过多地放在财富上，而是要多参与各种各样有趣的活动，制定不同的目标——不要只关注经济目标。

图4 幸福的两个面向。总体幸福由两类幸福组成——在生活中感到幸福（即时幸福感）和对人生感到幸福满足（生活满意度）。（A）在生活中感到幸福与即时享受相关，通常来自与喜欢的人共度时光。（B）对人生感到幸福满足（如满意度），即回顾自己以往生活时，发现目标已经完成。这两种幸福并非总是同时到来，智慧就在于找到两全之道[6]。

• 科学家宛若孩童，乐于改变自己的想法

对我来说，做一名科学家就是要像孩子一样，时刻保持高度的好奇心。当然，科学家们也不能完全理解周围的世界，但他们确实做出了极大的努力，试图去理解这个世界。作为一名科学家，我也乐于改变自己的想法。有些科学家很难改变观念，会死死抓着一个想法不放。而我跟他们恰恰相反，对我来说，只有转变思维才能学到新的东西。从这一点来看，深耕科学领域是一个不断循环的过程。“唉！我怎么这么笨？之前怎么没想到？”这样的时刻总会一次又一次地出现。这种重新看待事物的经历，在科学家的生活中比比皆是。如果你决定成为一名科学家，这种体验将贯穿你的一生。即使我已经88岁了，这种情况仍时有发生。 
致谢：感谢Noa Segev的采访和共同撰稿，本文基于这次采访完成。感谢Alex Bernstein绘制插图。

名词释义：

前景理论（PROSPECT THEORY），研究有风险的财务决策中人类行为的理论，来自行为经济学（经济学的一个分支）。

行为经济学（BEHAVIORAL ECONOMICS），经济学的一个分支，研究影响人们作出财务决策的因素。

价值函数（VALUE FUNCTION），描述人们对收益或损失的主观价值评估和客观价值之间的关系。

损失厌恶（LOSS AVERSION），同等收益的吸引力远远比不上对损失的厌恶感。例如，人们不愿参与损失和收益的金额和概率都相同的赌博。
作者简介：丹尼尔·卡尼曼（Daniel Kahneman）于2002年获得诺贝尔经济学奖，但他说他从未修过一门经济学课程。卡尼曼是以色列-美国籍认知心理学家，在普林斯顿大学任教。他于希伯来大学获得心理学和数学本科学位，曾在以色列国防部担任心理学家，后于加利福尼亚大学伯克利分校获得博士学位。他与多位经济学家合作开展行为经济学研究。他的作品《思考，快与慢》畅销全球。

参考文献

[1]Tversky, A., and Kahneman, D. 1974. Judgment under uncertainty: heuristics and biases: biases in judgments reveal some heuristics of thinking under uncertainty. Science 185:1124–31. doi: 10.1126/science.185.4157.1124 
[2]Kahneman, D., and Tversky, A. 1979. Prospect theory: an analysis of decision under risk. Econometrica 47:363–91. doi: 10.2307/1914185 [3]Kahneman, D., and Tversky, A. 2013. “Prospect theory: an analysis of decision under risk,” in Handbook of the Fundamentals of Financial Decision Making: Part I, eds L. C. MacLean and W. T. Ziemba (World Scientific Press). p.99–127. doi: 10.1142/9789814417358_0006 [4]Kahneman, D., and Tversky, A. 2013. “Choices, values, and frames,” in Handbook of the Fundamentals of Financial Decision Making: Part I, eds L. C. McLean and W. T. Ziemba (World Scientific Press). p.269–78. doi: 10.1142/9789814417358_0016[5]Tversky, A., and Kahneman, D. 1991. Loss aversion in riskless choice: a reference-dependent model. Quart. J. Econ.106:1039–61. doi: 10.2307/2937956[6]Kahneman, D., and Riis, J. 2005. Living, and thinking about it: two perspectives on life. Sci. Wellbeing 1:285–304. doi: 10.1093/acprof:oso/9780198567523. 003.0011[7]Kahneman, D., Schkade, D. A., Fischler, C., Krueger, A. B., and Krilla, A. 2010. “The structure of well-being in two cities: Life satisfaction and experienced happiness in Columbus, Ohio; and Rennes, France,” in International Differences in Well-Being, eds E. Diener, J. F. Helliwell, and D. Kahneman (Oxford University Press). p. 16–33. doi: 10.1093/acprof:oso/9780199732739.003.0002[8]Kahneman, D., Krueger, A. B., Schkade, D., Schwarz, N., and Stone, A. A. 2006. Would you be happier if you were richer? A focusing illusion. Science 312:1908–10. doi: 10.1126/science.1129688

（参考文献可上下滑动查看）

原文链接：https://kids.frontiersin.org/zh/articles/10.3389/frym.2022.1014522-zh?utm_source=wechat_sci&utm_medium=social&utm_content=nobelarticle_0328&utm_campaign=frymartpromchn

复杂经济学读书会第二季

经济学理论的发展与社会环境变化密切相关。一方面，伴随计算机的发展，相应的研究技术日渐成熟，例如非线性动力学、复杂网络、ABM等，为研究者提供了更强大的分析工具；另一个方面，对“均衡”的经济学的研究，不能够解释实际的经济现象，例如金融危机、创新产生的新的发展模式等，研究者开始重视经济学的“非均衡”现象，把经济系统看做复杂系统，并力图做出更能反映现实的研究。经济学内慢慢出现了一种基于更加现实的假设的研究进路，复杂经济学一个新的经济学框架正在形成。

复杂经济学读书会第二季由北京师范大学李红刚、王有贵、张江、陈清华老师以及中山大学袁先智老师联合发起，围绕复杂经济学的内涵、基本方法、普适规律、应用场景四个方面进行探讨。读书会已完结，现在报名可加入社群并解锁回放视频权限。

本季读书会详情与报名方式请参考：直面复杂系统，重识经济规律：复杂经济学读书会第二季启动

推荐阅读

1. 行为经济学：经济系统的行为主体是否理性？| 集智百科2. 提升科研人员的幸福感，从改写科学新闻标题开始3. 为何有人沉迷赌博？从非理性行为解读决策中的奖励-好奇冲突 | Nat.Comput.Sci.速递4. 张江：第三代人工智能技术基础——从可微分编程到因果推理 | 集智学园全新课程5. 龙年大运起，学习正当时！解锁集智全站内容，开启新年学习计划6. 加入集智，一起复杂！

点击“阅读原文”，报名读书会