素数分布规律又有新发现！赵宇飞学生与牛津教授合作成果

克雷西
2024-12-22
13:08:48

来源：量子位

克雷西 发自 凹非寺
量子位 | 公众号 QbitAI

赵宇飞高材生、哥伦比亚大学助理教授Mehtaab Sawhney（索尼），又为数学界贡献了一项重要成果——

与牛津大学教授Ben Green（格林）一起，证明了一项关于素数分布的新规律。

关键是证明中用到了与Gowers范数相关的技术，而Gowers范数一开始是拿来研究等差数列的，看上去和素数规律风马牛不相及。

甚至作者索尼自己也表示，“作为一个‘局外人’，几乎不可能判断出这些事情是相关的”。

所以，这项研究不仅在素数领域是一项重要工作，也揭开了高尔斯范数的应用潜能。

多伦多大学教授John Friedlander评价说，索尼和格林的这项研究表明高尔斯范数可以作为新领域的强大工具。

最早和陶哲轩一同将素数和Gowers范数联系到一起的数学家Tamar Ziegler（齐格勒），也对索尼和格林的研究给予了高度评价：

看到我前一段时间想到的东西有了意想不到的新应用，让我觉得很有趣。

证明素数分布新规律

2018年，Friedlander和美国罗格斯大学的Iwaniec提出了“高斯素数猜想”（Gaussian primes conjecture）：

存在无穷多个素数p、q，使得p²+4q²也是素数。

（Friedlander和Iwaniec的合作可以追溯到上个世纪，1997年他们一同证明了a²+b⁴可以组成无数个素数）

格林和索尼不仅证明了这一猜想，还将其推广到了更多的情况——

对于满足n≡0或n≡4(mod 6)的正整数n，均存在无穷多个素数p和q使得p²+nq²也是素数。

同时，格林和索尼还为这些素数的数量给出了渐近公式：

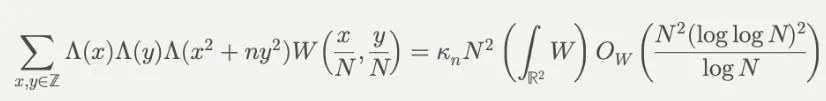
其中∧(n)是von Mangoldt函数，用于检测n是否为素数或素数的幂，N>1，W为权函数，κ_n是一个与n有关的常数：

显然，满足条件的素数数量不可能通过直接计算得到。

于是，格林和索尼选择先将要证明的结论弱化，也就是先放宽一下约束条件——先将p和q的范围放宽到“粗略素数”。

举个例子，如果我们要找出1-200之间的“粗略素数”，可以找到与2、3、5、7这几个小素数同时互素（最大公因数为1）的数，这些数字即为1-200之间的“粗略素数”。

（这些“粗略素数”当中，实际上不是素数的数，算上1也只有5个。）

格林和索尼证明，通过对两个“粗略素数”进行平方并将它们相加，可以得到无限多个素数。

接下来，他们就需要证明使用“粗略素数”构建的集合，和使用真实素数构建的集合“足够相似”。

其中就涉及了最关键的技术突破——Gowers范数的使用。

Gowers范数是一种测量函数“伪随机性”的工具，2001年由数学家蒂莫西·高尔斯（Timothy Gowers）提出。

2018年，陶哲轩和塔玛尔·齐格勒（Tamar Ziegler）找到了一种将高尔斯范数与“Type I和”与“Type II和”之间联系起来的方法。

具体到这项研究，作者首先通过筛法将问题简化为“Type I和”（左）与“Type II和”（右）的估计：

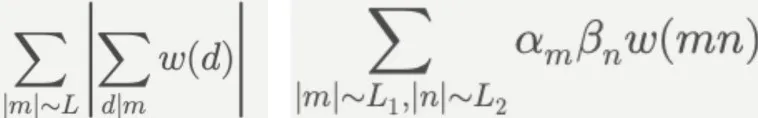
筛法的核心思想是，通过对这两类和的估计，过滤掉不满足素数条件的数，从而集中分析那些可能使p²+nq²为素数的数值。

其中，“Type I和”聚焦于单个变量的局部分布，帮助处理低阶贡献；“Type II和”则关注双变量交互，处理高阶分布。

进一步地，作者将问题转化到二次虚数域Q(√(-n))，并利用数域中的理想分解、范数分布以及素理想的性质来研究目标数列的素数性。

具体来说，在整数环Z中，研究x²+ ny²是否为素数，等价于在Q(√(-n))中分析主理想x+y√(-n)是否为素理想。

接下来就轮到Gowers范数登场了。

为了控制“Type II和”，论文定义了函数f(x)和f’(y)，其中∧_Cramér(x) 是von Mangoldt函数的低复杂度近似：

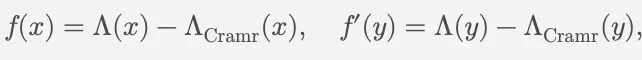
作者通过引入连接定理和逆定理，使用Gowers范数分析f(x)和f’(y)的伪随机性，从而证明了它们在大部分情况下对二次型x²+ ny²的贡献是可控的。

也就是说，作者通过筛法和Gowers范数，证明了关键的中间结果——x, y的组合分布是均匀的。

最终的表达式中，主项来源于数域中范数N(x+ y√(-n))的分布，利用数域的素理想定理，可以得到主项。

“Type I和”与“Type II和”带来的误差项，分别可以通过筛法分析和Gowers范数的均匀性假设来控制。

两者结合后，误差项对主项的影响是次级的。

将主项和误差项结合，最终得出目标公式：

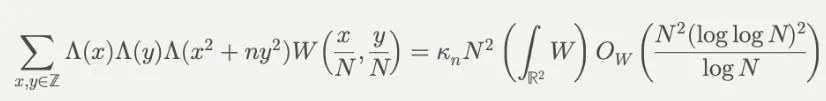
结缘于Gowers范数

这项研究的两位作者——格林和索尼，说起来也是颇有缘分。

格林是牛津大学数学教授、陶哲轩的长期合作者，同时还是英国皇家学会Fellow。

索尼一开始在宾夕法尼亚大学读计算机，然后在2017年转到MIT主修数学，成为了赵宇飞的学生，之后又在赵宇飞手下读博，并于今年6月毕业。

今年初索尼成为了克莱研究员，现在索尼在哥伦比亚大学担任教职。

让两人走到一起的，或许正是这次研究中用到的Gowers范数。

Gowers范数是1998年菲尔兹奖得主、英国数学家蒂莫西·高尔斯（Timothy Gowers）在证明塞迈雷迪定理时提出的。

塞迈雷迪定理与等差数列相关：

若一个整数集A具有正的自然密度，则对任意的正整数k，都可以在A中找出一个包含k项的等差数列。

所谓具有正自然密度，就是当n趋于无穷时，A与1,2,…,n这个数列的交集中元素个数与n的比值大于0。

到了2017年，陶哲轩和格林一起给出了k=4时的新上界。

2022年，正在陶哲轩那里读研二的James Leng（小冷）开始研究起了高尔斯的理论，并引起了索尼和他的师弟Ashwin Sah（小萨）的注意。

最终，三人共同把这一结论推广到了k为任意取值的情况，成为了23年以来在这个问题上最重大的突破。

与这次索尼和格林的研究一样，三人在其中也使用了Gowers范数的逆定理，并且这项逆定理的发现者正是索尼、小冷和小萨。

顺便提一句，打从本科起，索尼和小萨就是彼此的科研搭子，关系密切到索尼主页列出的70篇论文里，有60篇都带小萨的名字。

而导师赵宇飞在本科时对他俩的评价就是：

（MIT）的本科生研究有着悠久的历史和传统，但在论文的质量和数量上，都达不到Ashwin Sah和Mehtaab Sawhney的水平。

说回索尼本人，今年七月，索尼和格林终于在爱丁堡的一次会议上会面。

索尼说自己一直非常欣赏格林，并表示格林20年前证明的一项开创性成果正是让他选择这个主题的原因之一。

格林也对这位年轻的数学家印象深刻，称索尼是一位杰出的数学家，并“以某种方式知道一切”。

于是，两人决定合作，并将目光聚焦在了这次的“高斯素数猜想”。

到牛津访问一周后，索尼和格林对其证明有了思路，并于今年10月份发布了论文预印本。

此后，两人又继续合作，提出并证明了Furstenberg-Sárközy定理的改进界限。

论文地址：
https://arxiv.org/abs/2410.04189
参考链接：

Mathematicians Uncover a New Way to Count Prime Numbers

Read More