兼得快与好!训练新范式TiM,原生支持FSDP+Flash Attention
双杀两大难题
TiM团队 投稿
量子位 | 公众号 QbitAI
生成式AI的快与好,终于能兼得了?
从Stable Diffusion到DiT、FLUX系列,社区探索了很多技术方法用于加速生成速度和提高生成质量,但是始终围绕扩散模型和Few-step模型两条路线进行开发,不得不向一些固有的缺陷妥协。
这便是训练目标引发的“生成质量”与“生成速度”之间的矛盾根源:
要么只监督无穷小局部动力学(PF-ODE),要么只学习有限区间的端点映射,两者都各有内在限制。
一项新研究提出了名为Transition Model(TiM)的新范式,试图从根本上解决这一矛盾。
它放弃了传统扩散模型学习“瞬时速度场”或Few-step模型学习“端点映射”的做法,转而直接建模任意两个时间点之间的完整状态转移。
这意味着TiM在理论上支持任意步长的采样,并能将生成过程分解为多段粒度可灵活调整的细化轨迹
什么是Transition Model?
为什么说“PF-ODE”与“概率分布匹配”对于生成模型都不是理想的训练目标?
来看扩散模型,它以迭代去噪获得高保真,在于它学习的是PF-ODE的局部向量场,训练时只对无穷小时间步的瞬时动力学做监督,采样时必须用很小步长或高阶多步求解器来压离散误差,导致NFEs居高不下。
又比如少步生成(如 Consistency/Shortcut/Distillation/Meanflow)虽快,但因为没有刻画中间动力学,增步后收益很快饱和,常遭遇 “质量天花板”,增加步数反而不再带来收益,生成能力上限不及扩散模型。
这些固有的缺陷来源于模型训练过程中监督信号的引入方式,或是求解局部的PFE方程,或是匹配固定的概率分布;换句话说,生成过程中,模型做出预测被clean data所监督的粒度,直接决定了模型在推理过程中的离散误差和生成质量上限。
所以,对于生成模型,什么才是一个合适的训练目标呢?
从扩散模型与Few-step模型的训练目标的局限性出发,可以得到以下分析——
局部(无穷小)监督:PF-ODE/SDE类目标。
这类目标只在极小时间步上拟合瞬时动力学(Δt→0),要想维持连续时间解的精度,采样时就必须用很小步长/很多步,于是NFEs很高;一旦把步数压到很少,质量就会明显掉队。
因此,对于能够带来高保真度的局部监督信号而言,时间区间,或者说单步步长理想情况下应该是要能灵活改
全局端点监督:few-step/一致性/蒸馏一类目标/mean-flow/short-cut。
这类训练目标学习固定跨度的端点映射(或者平均速度场),核心是一步 “吃掉” 整段轨迹,因而少步很强;但因为 “把整条轨迹平均化”,细节动力学被抹掉,再加步也难以继续提升——出现质量饱和。
因此,训练目标应该要求沿轨迹保持一致,要存在中间步骤充当单个轨迹的细化,而不是偏离新的轨迹,这使得sampler对采样规划不敏感,并能够通过更多步骤实现稳定的质量改进。
因此,一个能兼得快速生成(few-step)与高保真度生成(扩散模型)的训练目标应该是:
在“多段细化轨迹”里实现“灵活的单步尺寸”(任意步长),这便是Transition Model。
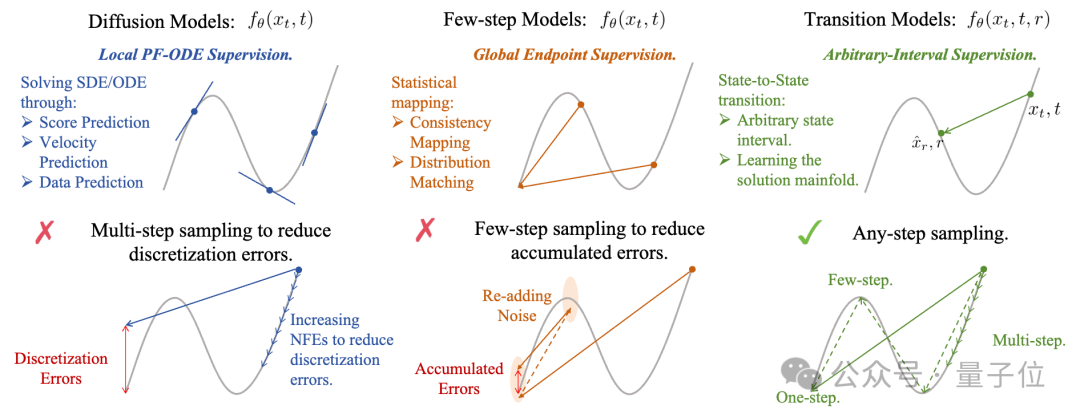
想要兼得推理速度与高保真度质量,需要一个核心设计,“在多段细化的轨迹”里面实现“灵活的单步尺寸”。
这一工作基于此设计了Transition Model:
将模型的训练从单一时刻t,拓展到建模任意两个时刻t与r的状态x_t, x_r.
设计1:实现“灵活的单步尺寸”
对于给定的两个时刻t与r之间的状态转移,通过化简其微分方程得到了“通用状态转移恒等式”(State Transition Identity);基于通用状态转移恒等式,得以描述任意的一个时间间隔内的具体状态转移,而不是作为数值拟合求解。
设计2:实现“多段细化轨迹的生成路径”
在设计1中,已经实现了任意步长 (任意时间间隔), 因此对于多段细化轨迹的生成路径,这个方法就可以直接的描述任意时刻t下对于此前任意时刻r之间的状态转移,那么“多段细化的生成路径”就变成了“任意状态与前状态之间的状态转移动态 (state transition dynamics)”,这样就能在保持快速生成的同时保证高保真度的生成质量。
通过设计1和设计2,这篇文章提出的Transition Model将“在任意状态下,任意时间间隔内,与前状态之间的状态转移的动力学方程”作为训练目标,它就满足了兼得推理速度与高保真度质量的核心设计。
Transition Model的数学本质
Diffusion model是建模瞬时速度场,局限性是瞬时速度需要时间区间趋近于0;
Meanflow核心是建模平均速度场,局限性是平均速度丢了局部优化的dynamics细节,生成质量早早收敛,过了few-step后近乎为定值;
不同于前两者,Transition Model做的是任意时间区间的任意状态间的状态转移,可以认为是任意速度场,自然而然地包含了瞬时速度和平均速度;
从解的形式上讲 Diffusion是局部PF-ODE的数值解,meanflow是局部平均速度场中的解集,transition model求的是全局生成路径上的解的流型,special case情况下可以退化为平均速度场,解的流型退化为局部解集。

作者们主要在图文生成(Text-to-Image)任务上进行了验证。
在Geneval数据集上,分别比较了Transition Model在不同推理步数(NFE), 不同分辨率,不同横纵比下的生成能力:
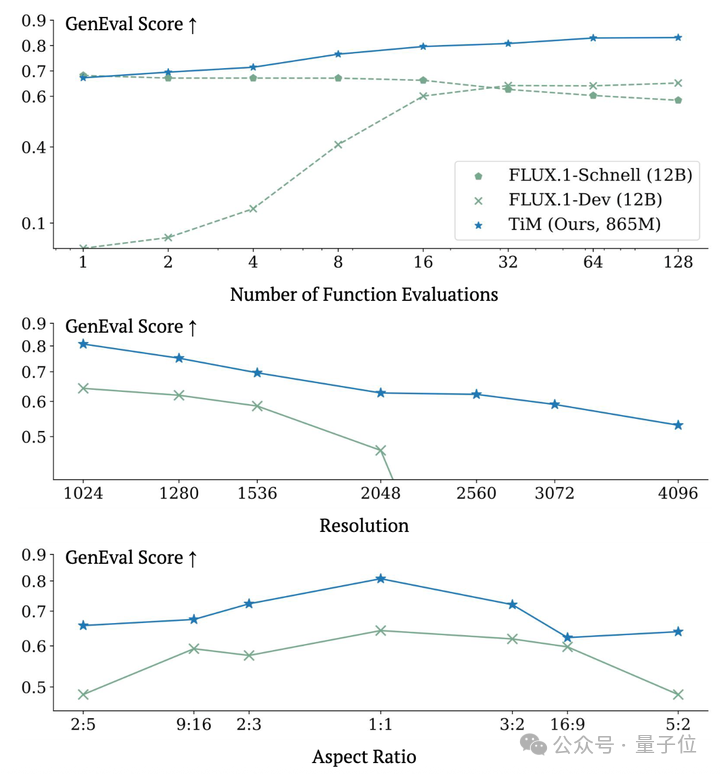
这篇文章发现865M参数大小的Transition Model(TiM)可以在明确地超过FLUX.1-Schnell(12B参数)这一蒸馏模型;与此同时,在生成能力上限上也可以超过FLUX.1-Dev(12B参数)。
并且由于TiM结合了Native-Resolution预训练的训练策略(详见Native-Resolution Image Synthesis),这篇文章所提出的模型在分辨率和横纵比上也更加灵活。
Transition Model的训练稳定性与扩展性
让Transition Model训练具有可扩展性.
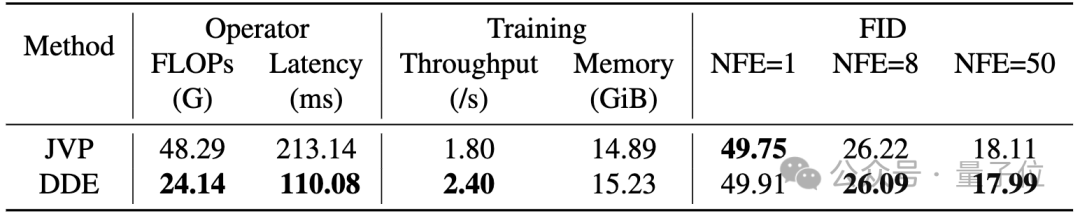
在Transition Model的训练过程中,它的训练目标的关键在于计算网络关于时间的导数$frac{mathrm{d} f_{theta^{-}, t, r}}{mathrm{d} t}$。
以MeanFlow和Short-cut Model为代表的既有方法通常依赖雅可比—向量乘积(JVP)来完成这一计算。
然而,JVP在可扩展性上构成了根本性瓶颈:
不仅计算开销高,更麻烦的是它依赖Backward自动微分,这与诸如FlashAttention和分布式框架Fully Sharded Data Parallel (FSDP) 等关键训练优化并不兼容,致使基于JVP的方法难以实际用于十亿参数级的基础模型训练。
为此,他们提出差分推导方程(DDE),用一种有原则且高效的有限差分近似来突破该限制:
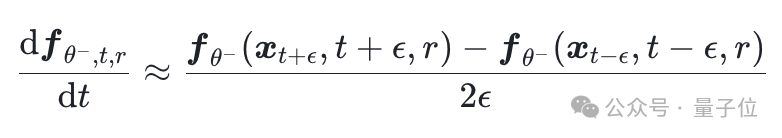
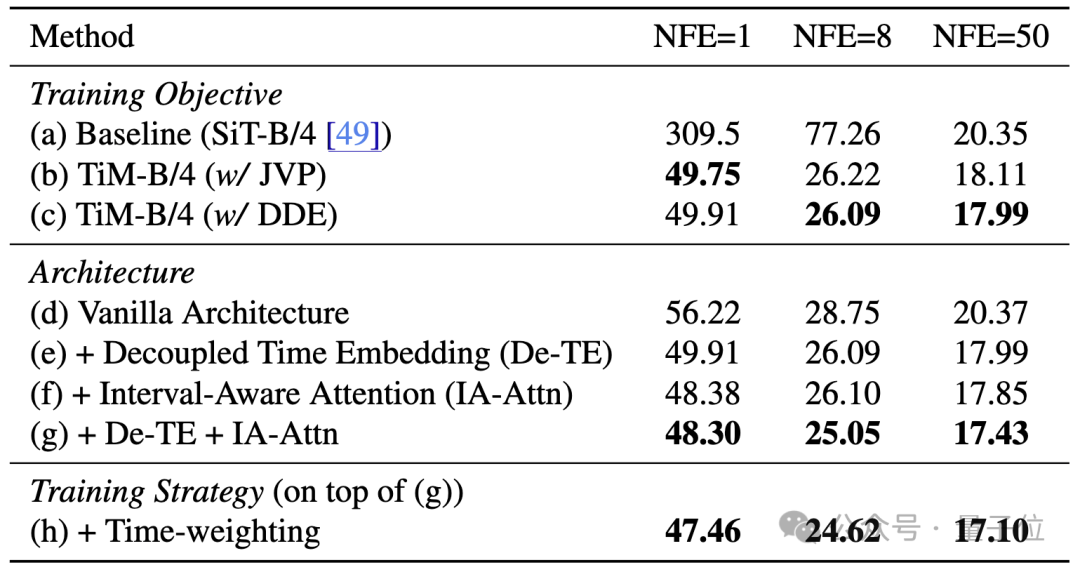
如表中所示,这篇文章所提出的DDE计算方式不仅比JVP约快2倍,更关键的是其仅依赖前向传播,与FSDP天然兼容,从而将原本不可扩展的训练流程变为可大规模并行计算的方案.
让Transition Model训练更加稳定.
除了可扩展性,基于任意时间间隔训练的另一大挑战是控制梯度方差。
比如,当转移跨越很大的时间间隔($Delta t to t$)时,更容易出现损失突增。
为缓解这一问题,作者们引入一种损失加权策略,优先考虑短间隔转移——这类转移更为常见,也能提供更稳定的学习信号。

其中,$tau(cdot)$是对时间轴进行重新参数化的单调函数。
在这篇文章最终模型中,他们采用正切空间变换(tangent space transformation来有效拉伸时间域,从而得到具体的加权形式:
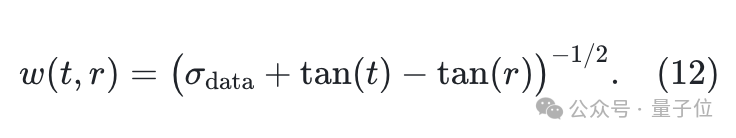
其中,$sigma_{text{data}}$表示干净数据(clean data)的标准差,这一方法有效地提升了训练的稳定性。
研究团队提出了Transition Model (TiM)作为生成模型的新的范式:
不再只学习瞬时向量场或固定跨度的端点映射,而是直接建模任意两时刻间的状态转移,用“通用状态转移恒等式”支撑任意步长与多段细化轨迹,从而兼顾少步速度与高保真质量。
在理论上,从学习生成路径上特定的解拓展到学习全局生成路径的解的流形;在实践上,通过DDE的前向有限差分替代JVP,原生兼容 FSDP/FlashAttention、训练更快更可扩展;同时用时间重参化+核函数的损失加权优先短间隔,降低梯度方差、提升稳定性。
实验表明,TiM-865M在多分辨率与多横纵比设置下,少步即可超越 FLUX.1-Schnell/Dev(12B)的速度-质量权衡。
总体而言,TiM以全局路径视角尝试解决“速度与质量难两全”的根本矛盾,提供了更通用、可扩展且稳定的生成建模。




 ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง
ufabet
มีเกมให้เลือกเล่นมากมาย: เกมเดิมพันหลากหลาย ครบทุกค่ายดัง







