中国数学家再中数学四大刊，兰州大学首篇：突破斯托克斯方程“光滑性”限制

闻乐
2025-10-22
14:33:55

来源：量子位

鱼羊 闻乐 发自 凹非寺

量子位 | 公众号 QbitAI

兰州大学刚出了篇数学四大刊！

作者是兰州大学耿俊教授和西湖大学申仲伟教授，论文已经被Inventiones mathematicae（《数学新进展》）接收。

《数学年刊》、《数学学报》、《数学新进展》和《美国数学会杂志》并称为数学四大刊，是国际数学界公认的数学顶级期刊，每年中国研究机构中选论文经常不超过10篇。

这项研究，围绕的是流体力学的重要基础之一：斯托克斯方程。

具体来说，是研究斯托克斯算子在非光滑区域里的无穷范数预解估计。

——别慌，咱浅浅地做个简化翻译，大概意思就是，两位数学家想搞清楚，在边界不那么规则的空间里，比如自然河道而非光滑的管道中，流体运动相关的数学方程解的范围和规律。

可以理解为，是为斯托克斯方程在相当广的范围内找到了更通用的数学规律。

这也是兰州大学首篇数学四大。

揭示斯托克斯方程在非光滑域内更普适规律

两位数学家瞄准的是流体力学理论里的一个关键缺口：

描述粘稠流体运动的斯托克斯方程，在非光滑边界空间里，流体的速度和压力还没有找到可靠的最大值约束规律。

△斯托克斯方程定常形式

在知道作用在粘稠流体上的外力有多大之后，要想算出流体的速度和内部压力，最关键的是搞清楚：能不能只通过外力的最大强度，就确定出流体速度的最大值、进而通过间接方式约束压力波动。

这个判断方法就是无穷范数

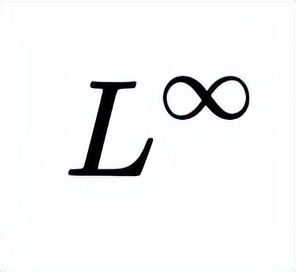
预解估计。

此前，依据如下公式，仅能在边界光滑的区域，比如完美的球面实现这一估计。

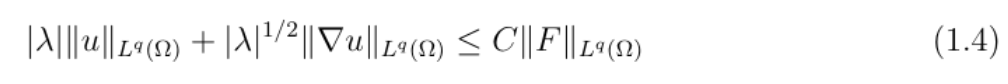
而现实中的工业管道接口并不完全光滑，比如常见的，有连续切线的C¹边界，允许棱角的Lipschitz边界等，会导致速度梯度和压力在边界附近失控，导致传统方法失效。

这篇论文有两大核心突破：

一是给出了关键结论，在3维及以上空间的C¹边界、2维空间的Lipschitz边界下，通过外力最大值，就能预估速度最大值。明确了非光滑边界的适用性。

二是用大尺度平均的创新思路破解了压力失控的难题。

具体来说，在有界区域中，3维及以上空间的C¹边界、2维空间的Lipschitz边界下，能得出如下核心结论：

最大速度

常数·最大外力。

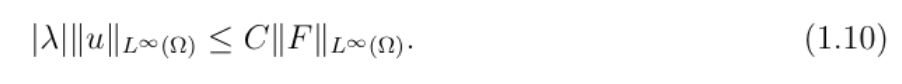
如果边界光滑，如C¹ˌᵅ，还能进一步通过如下公式控制速度梯度的最大值。

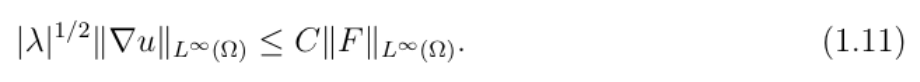
而对于外部的无界区域，只要

足够大，也能实现类似的速度控制，且2维Lipschitz边界下还得到了更完整的

预解估计。

在压力失控的问题上，作者并没有直接解决“点上压力难以控制”这个传统难题，而是巧妙地采用了“大尺度平均”的新思路：

不纠结边界附近极小尺度的压力波动，只在

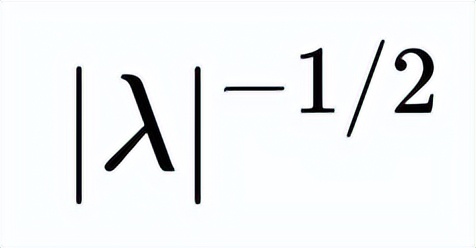
的合适大尺度的上分析，通过新的最大函数工具，

将压力的平均波动和速度的平均大小绑定。

再结合已有的

分析框架，最终实现

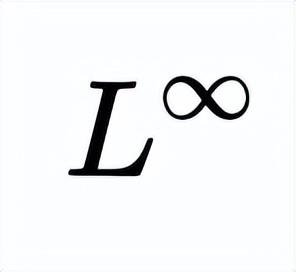
估计。

并用如下公式清晰地呈现了这一约束逻辑。

该研究的价值极具份量。

在理论上，填补了斯托克斯方程在非光滑区域无穷范数空间预解估计的研究空白，首次明确了C¹、Lipschitz边界的适用性，建立了相应的解析半群理论，完善了流体力学的数学分析体系。

在实际应用层面，为工程领域提供了更贴近现实的计算工具。

现实流体场景多为非光滑边界，在此之前，工程师依赖近似简化计算的误差较大，而本篇论文中的公式可以直接用于预估非光滑边界下的速度上限和压力变化范围，提高了数值的准确性。

东西部数学家联手

论文的两位作者，分别来自西部和东部重点研究机构兰州大学和西湖大学。

耿俊，出生于1982年，云南宣威人，现任兰州大学数学与统计学院教授、博士生导师。

他的主要研究方向是调和分析、偏微分方程，以及非光滑区域上的边值问题和均匀化理论等。

兰州大学的同学们可能还上过他开设的偏微分方程相关课程。

耿俊于2011年在美国肯塔基大学取得博士学位，导师正是论文的另一位作者申仲伟教授。

此前，师生二人已经合作过多篇颇具影响力的文章。

申仲伟，美国数学会首届会士，1964年出生，湖南衡阳人。

少时，申仲伟就有“天才少年”之名——14岁就考进了北大数学系。

1985年，他硕士毕业于中国科学院数学研究所。1989年获芝加哥大学数学博士学位。在加入肯塔基大学之前，申仲伟还曾在普林斯顿大学和普渡大学任教。

1995年，申仲伟入职肯塔基大学数学系，2003年晋升为正教授，并于2007-2011年担任数学系系主任。2016年，他还获得了肯塔基大学文理学院杰出教授称号。

而就在今年7月，申仲伟选择回国全职任教，加盟西湖大学理学院、理论科学研究院，担任数学讲席教授。

他的学生中，耿俊之外，诸葛金平也已回国任教，现任中国科学院晨兴数学中心副研究员。

论文地址：
https://arxiv.org/abs/2408.03844

— 完 —

Read More