DeepSeek再破谷歌OpenAI垄断：开源IMO数学金牌大模型

henry
2025-11-28
12:43:20

来源：量子位

henry 发自 凹非寺

量子位 | 公众号

AI界掌管开源的神——DeepSeek回来了！

刚刚，DeepSeek开源了全新的数学模型DeepSeekMath-V2，专注于可自验证的数学推理。

DeepSeekMath-V2不仅在IMO 2025和CMO 2024中取得金牌级分数，而且还在Putnam 2024中，得分118/120，超过了人类最高分90。

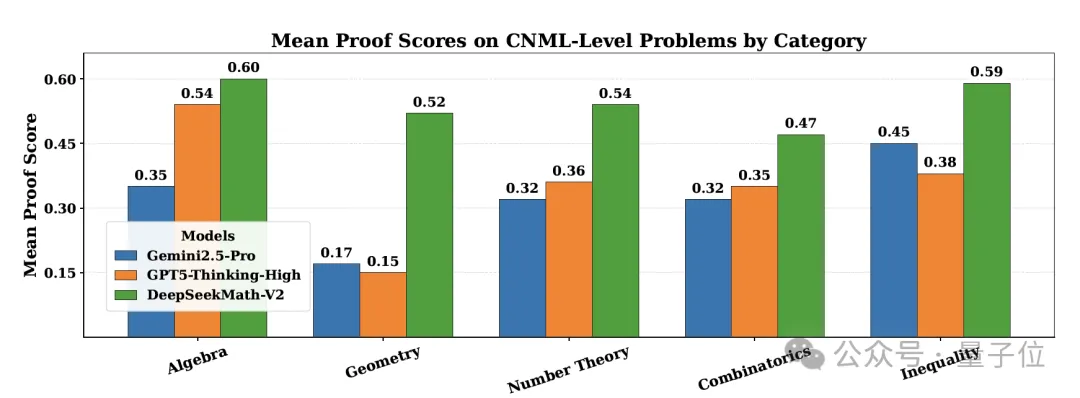
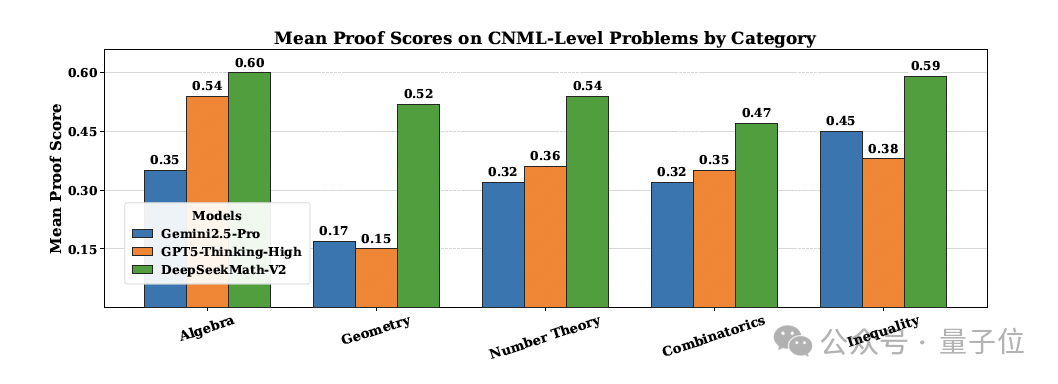
与此同时，DeepSeekMath-V2在所有CNML级别问题类别（代数、几何、数论、组合学、不等式）上均优于GPT-5-Thinking-High和Gemini 2.5-Pro。

不仅性能无敌，网友表示这还是第一个开源的IMO金牌模型。

这下，谷歌和OpenAI要坐不住了！

特别是OpenAI，本来就打算放出IMO金牌模型来应对谷歌Gemini 3 Pro的冲击，现在被DeepSeek抢先一步。

（鲸鱼回来了！）

值得一提是，这篇论文的一作邵智宏也是之前DeepSeekMath 7B的一作，在那篇论文中，他们提出了著名的GRPO。

最强开源IMO金牌模型

总的来说，DeepSeekMath-V2是一个旨在实现自验证数学推理（Self-verification）的大型语言模型（685B）。

它的核心在于开发和利用强大的证明验证能力来指导和优化证明生成，从而克服传统上依赖最终答案作为奖励的强化学习（RL）方法的局限性。

传统用于数学推理的强化学习（RL）方法存在根本性限制：

• 最终答案奖励的不可靠性：将LLM奖励基于最终答案的正确性，并不能保证推理过程的正确性或逻辑的严谨性，模型可能通过错误的逻辑得出正确答案 。
• 对定理证明任务的局限性：许多数学任务（如定理证明）不要求数值答案，而是需要严格的步骤推导和逻辑严谨性，使得基于最终答案的奖励机制不适用。
• 缺乏内部验证能力：经过传统方法训练的LLMs缺乏验证自身证明有效性的能力，经常表现出高假阳性率（即认为错误的证明是有效的)。

DeepSeekMath-V2采用迭代的强化学习循环，交替优化证明验证器和证明生成器，以实现可自验证的数学推理。

证明验证

训练验证器

研究首先训练一个准确且忠实的LLM-based验证器，使其能够根据人类专家的标准识别证明中的问题并评分。

具体来说，验证器针对给定的数学问题与证明，输出一个证明分析，该分析首先总结识别出的问题（如果有），然后基于三个级别分配一个分数：

1：完全正确、严谨且逻辑清晰的证明。0.5：总体逻辑合理，但有微小错误或细节遗漏的证明。0：包含致命逻辑错误或关键漏洞的根本性错误的证明。

验证器的训练分为数据构建（冷启动）和模型强化学习目标两个关键阶段。

在数据构建阶段，研究首先从AoPS竞赛中收集了1.75万个要求证明的奥赛级别数学问题。

随后，利用现有模型（DeepSeek-V3.2-Exp-Thinking）生成大量的候选证明，并通过多轮迭代来提升证明的严谨性，最终请数学专家人工对这些证明进行评分，分数分为1、0.5和0三个级别，从而创建了初始的RL验证数据集。

进入强化学习目标阶段，研究使用上述数据集对基础模型（DeepSeek-V3.2-Exp-SFT）进行训练，使其能够输出证明分析总结和最终分数。

奖励函数一方面通过格式奖励强制模型输出格式包含问题总结和分数，另一方面通过分数奖励激励模型预测的分数与专家标注的分数高度一致，从而使验证器具备模仿人类专家评估严谨性的能力。

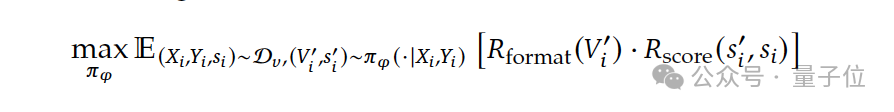
引入元验证 (Meta-Verification)

为解决初步训练的验证器可能因幻觉（hallucinating）不存在的问题而获得正确低分，从而损害其对错误识别的忠实性（faithfulness）的问题，研究团队引入了元验证（Meta-Verification）机制。

元验证作为一个二级评估过程，旨在审查验证器生成的证明分析（Proof Analysis），评估其中识别出的问题是否真实存在，以及这些问题是否在逻辑上合理地支持了其预测的证明分数。

为了训练元验证器，研究首先让数学专家根据专门的元验证标准对验证器输出的分析质量进行评分，创建了元验证数据集。

随后，研究训练了一个专门的元验证器，该元验证器生成对验证分析本身的问题总结，并分配一个质量分数，以衡量原验证器分析的准确性和合理性。

元验证器的强化学习目标结构与验证器训练类似，同样包含格式奖励和分数奖励。

接下来是增强验证器训练，研究利用训练好的元验证器，将元验证的质量分数集成到验证器的奖励函数中，以增强验证器的忠实性。

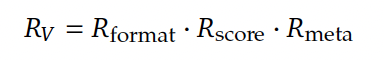
最终，使用原验证数据集和元验证数据集共同训练增强后的验证器，使该模型能够同时执行证明验证和元验证两项任务。

在原验证数据集的一个验证子集上，经验证器评估的证明分析的平均质量分数从 0.85 提升到了0.96，同时保持了证明分数预测的准确性不变，有力证明了元验证机制能有效提高验证器识别问题的忠实度。

证明生成

接下来，研究用训练好的验证器作为奖励模型来训练证明生成器，并进一步通过“自验证”机制，让生成器学会严格地自我审查和修正，从而提高证明质量。

具体来说，研究训练生成器以最大化验证器赋给其生成的证明的分数。

在训练中，生成器被要求在生成证明后，紧跟着进行自我分析。奖励函数激励准确的自我评估和正确性。

最终奖励是对证明质量和自我评估质量的加权组合。

由此，自我评估奖励不仅奖励自评分的准确性，还奖励自我分析的忠实性。

这种奖励结构激励生成器：忠实地承认错误（而非盲目自信）。获得高奖励的最佳策略是在最终输出前，积极识别并解决自身证明中存在的问题，从而实现自我迭代完善。

证明验证与生成之间的协同作用

接下来，研究利用验证器和生成器的协同作用，通过规模化的计算和元验证机制，建立了一个完全自动化的数据标注流程，从而持续提升验证器的能力，并最终取代耗时的人工标注。

然而，随着问题难度增加，人工标注耗时且效率低下。由此研究提出了一套自动化标注的方法：

首先，通过生成n个独立的验证分析，提高在有缺陷证明中捕获真实问题的概率。接下来，利用元验证器生成m个评估，对报告问题的分析进行有效性确认，确保识别出的问题是真实的（元验证比从零识别问题更高效）。

具体的标注流程如下：

• 分数判定：检查所有分析中分配的最低分数。只有当至少有k个分析被元验证确认为有效时，该最低分才被赋给该证明；否则标记为1分（无合法缺陷）。
• 取代人工： 最终，这种完全自动化的流程在后续训练迭代中彻底取代了人工标注，并且质量检查证实其标注结果与专家判断高度一致。

由此，上述流程在最终的训练迭代中彻底取代了耗时的人力标注，实现了验证和生成的协同循环，保证了模型能力的持续突破。

实验结果

研究采用GRPO进行强化学习，迭代地优化证明验证和生成能力。

在每次迭代中，研究首先优化证明验证。然后，证明生成器会从验证器的checkpoint初始化，并针对证明生成进行优化。

从第二次迭代开始，证明验证器会使用一个检查点进行初始化，该检查点通过拒绝微调（rejection fine-tuning）巩固了前一次迭代中的验证和生成能力。

研究首先评估了模型未经迭代完善的单次生成正确证明的能力。

实验结果表明，在所有CNML级别问题类别中——包括代数、几何、数论、组合学和不等式——DeepSeekMath-V2 持续优于 GPT-5-Thinking-High和Gemini 2.5-Pro。

为了探究扩展上下文和自验证如何提高证明质量，研究又评估了带有自验证的顺序精炼方法。

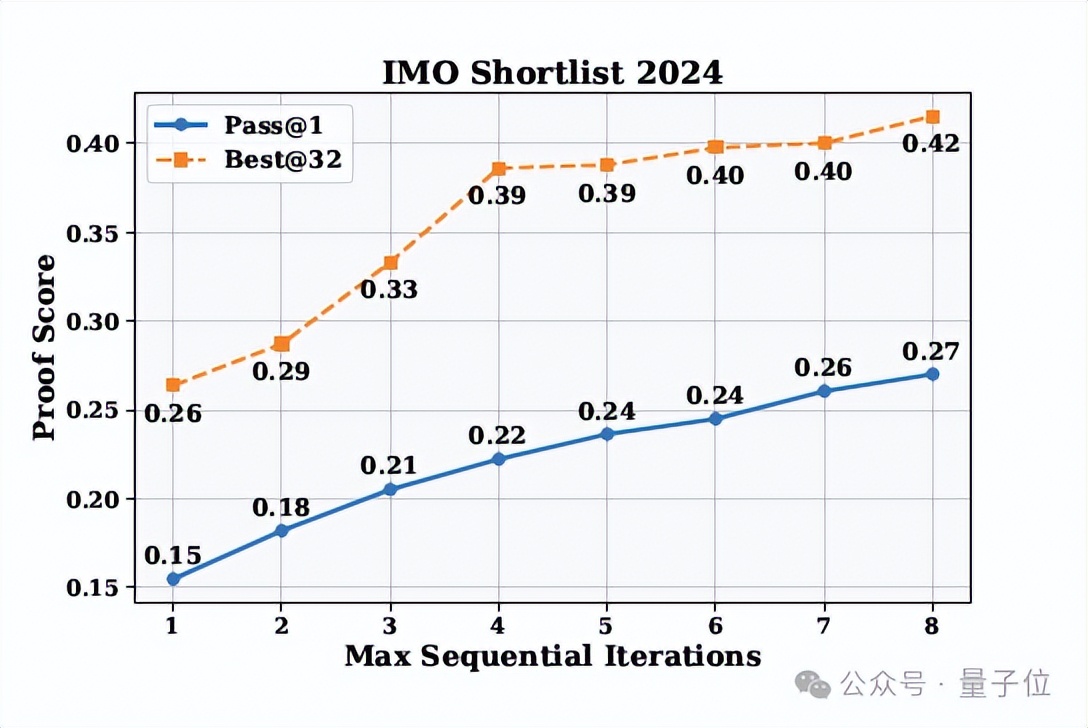
研究表明，自选的最佳证明比线程平均得分获得了显著更高的验证分数，这证明生成器具备准确评估证明质量的能力。

此外，随着最大顺序尝试次数的增加，Pass@1大幅提升，表明自验证有效地指导了迭代改进。

这些结果表明，生成器能够可靠地区分高质量和有缺陷的证明，并利用这种自我意识系统地改进其数学推理。

最后，为了解决最具备挑战性的问题，研究采用了高计算量搜索策略，该策略通过并行生成探索多样化的证明路径，并结合规模化的（64 次）验证来精确识别细微错误。

模型迭代地从包含问题分析的候选证明池中精炼出最优证明，直到证明通过所有验证。

最终，这种方法使其在Putnam竞赛中以118/120的分数超越人类最高分90分，展现了在验证器指导下，AI解决复杂问题的强大能力。

One more thing

如开头所说，这篇论文的一作邵智宏也是DeepSeek之前数学模型DeepSeekMath 7B的一作。

值得一提的是，也就是在DeepSeekMath 7B的论文中，他和团队提出了经典的GRPO（Group Relative Policy Optimization ）。同样的，他也是DeepSeek-R1的核心贡献者。

邵智宏目前是DeepSeek从事大模型推理研究的研究员，他本科毕业于北京航空航天大学，博士毕业于清华，师从黄民烈教授。

参考链接

[1] https://huggingface.co/deepseek-ai/DeepSeek-Math-V2

[2]https://github.com/deepseek-ai/DeepSeek-Math-V2/blob/main/DeepSeekMath_V2.pdf

[3]https://zhihongshao.github.io/

Read More